Walk in Graph Theory | Path | Trail | Cycle | Circuit

Walk in Graph Theory-

 

In graph theory,

• A walk is defined as a finite length alternating sequence of vertices and edges.
• The total number of edges covered in a walk is called as Length of the Walk.

 

Walk in Graph Theory Example-

 

Consider the following graph-

 

 

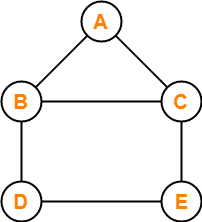
In this graph, few examples of walk are-

• a , b , c , e , d                    (Length = 4)
• d , b , a , c , e , d , e , c     (Length = 7)
• e , c , b , a , c , e , d          (Length = 6)

 

Open Walk in Graph Theory-

 

In graph theory, a walk is called as an Open walk if-

• Length of the walk is greater than zero
• And the vertices at which the walk starts and ends are different.

 

Closed Walk in Graph Theory-

 

In graph theory, a walk is called as a Closed walk if-

• Length of the walk is greater than zero
• And the vertices at which the walk starts and ends are same.

 

NOTE   It is important to note the following points- If length of the walk = 0, then it is called as a Trivial Walk. Both vertices and edges can repeat in a walk whether it is an open walk or a closed walk.

 

Path in Graph Theory-

 

In graph theory, a path is defined as an open walk in which-

• Neither vertices (except possibly the starting and ending vertices) are allowed to repeat.
• Nor edges are allowed to repeat.

 

Cycle in Graph Theory-

 

In graph theory, a cycle is defined as a closed walk in which-

• Neither vertices (except possibly the starting and ending vertices) are allowed to repeat.
• Nor edges are allowed to repeat.

 

OR

In graph theory, a closed path is called as a cycle.

 

Trail in Graph Theory-

 

In graph theory, a trail is defined as an open walk in which-

• Vertices may repeat.
• But edges are not allowed to repeat.

 

Circuit in Graph Theory-

 

In graph theory, a circuit is defined as a closed walk in which-

• Vertices may repeat.
• But edges are not allowed to repeat.

OR

In graph theory, a closed trail is called as a circuit.

 

NOTE   It is important to note the following points- Every path is a trail but every trail need not be a path. Every cycle is a circuit but every circuit need not be a cycle. For directed graphs, we put term “directed” in front of all the terms defined above.

 

Important Chart-

 

The following chart summarizes the above definitions and is helpful in remembering them-

 

 

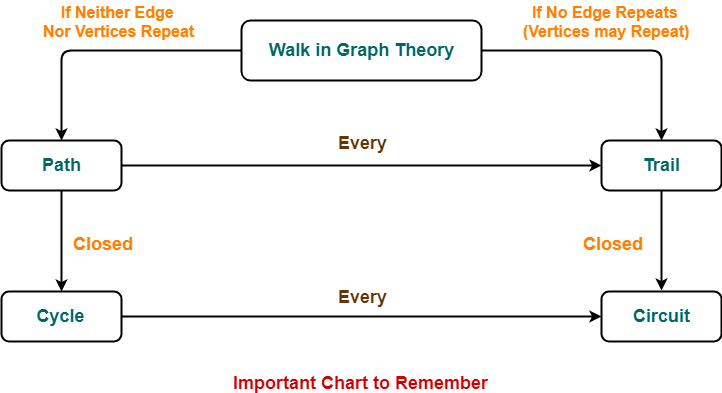
Also Read- Types of Graphs in Graph Theory

 

PRACTICE PROBLEMS BASED ON WALK IN GRAPH THEORY-

 

Problem-01:

 

Consider the following graph-

 

 

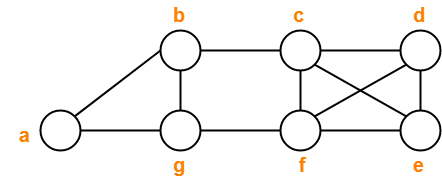
Decide which of the following sequences of vertices determine walks.

For those that are walks, decide whether it is a circuit, a path, a cycle or a trail.

1. a , b , g , f , c , b
2. b , g , f , c , b , g , a
3. c , e , f , c
4. c , e , f , c , e
5. a , b , f , a
6. f , d , e , c , b

 

Solution-

 

1. Trail
2. Walk
3. Cycle
4. Walk
5. Not a walk
6. Path

 

Problem-02:

 

Consider the following graph-

 

 

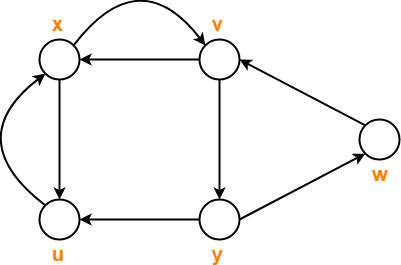
Consider the following sequences of vertices and answer the questions that follow-

1. x , v , y , w , v
2. x , u , x , u , x
3. x , u , v , y , x
4. x , v , y , w , v , u , x

 

1. Which of the above given sequences are directed walks?
2. What are the lengths of directed walks?
3. Which directed walks are also directed paths?
4. Which directed walks are also directed cycles?

 

Solution-

 

Part-01:

 

• Only (A) and (B) are the directed walks.
• (C) is not a directed walk since there exists no arc from vertex u to vertex v.
• (D) is not a directed walk since there exists no arc from vertex v to vertex u.

 

Part-02:

 

Both the directed walks (A) and (B) have length = 4.

 

Part-03:

 

• Neither (A) nor (B) are directed paths.
• This is because vertices repeat in both of them.
• Vertex v repeats in Walk (A) and vertex u repeats in walk (B).

 

Part-04:

 

• Neither of them are directed cycles.
• Walk (A) does not represent a directed cycle because its starting and ending vertices are not same.
• Walk (B) does not represent a directed cycle because it repeats vertices/edges.

 

Problem-03:

 

Consider the following graph-

 

 

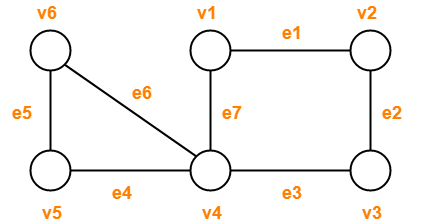
Observe the given sequences and predict the nature of walk in each case-

1. v1e1v2e2v3e2v2
2. v4e7v1e1v2e2v3e3v4e4v5
3. v1e1v2e2v3e3v4e4v5
4. v1e1v2e2v3e3v4e7v1
5. v6e5v5e4v4e3v3e2v2e1v1e7v4e6v6

 

Solution-

 

1. Open walk
2. Trail (Not a path because vertex v4 is repeated)
3. Path
4. Cycle
5. Circuit (Not a cycle because vertex v4 is repeated)

 

To gain better understanding about Walk in Graph Theory,

Watch this Video Lecture

 

Next Article- Graph Coloring

 

Get more notes and other study material of Graph Theory.

Watch video lectures by visiting our YouTube channel LearnVidFun.