Go Back N Protocol-
Before you go through this article, make sure that you have gone through the previous article on Go back N Protocol.
We have discussed-
- Sliding window protocols allow the sender to send multiple frames before needing acknowledgements.
- Go back N is an implementation of a sliding window protocol.
In this article, we will discuss practice problems based on Go back N protocol.
PRACTICE PROBLEMS BASED ON GO BACK N PROTOCOL-
Problem-01:
A 20 Kbps satellite link has a propagation delay of 400 ms. The transmitter employs the “go back n ARQ” scheme with n set to 10.
Assuming that each frame is 100 bytes long, what is the maximum data rate possible?
- 5 Kbps
- 10 Kbps
- 15 Kbps
- 20 Kbps
Solution-
Given-
- Bandwidth = 20 Kbps
- Propagation delay (Tp) = 400 ms
- Frame size = 100 bytes
- Go back N is used where N = 10
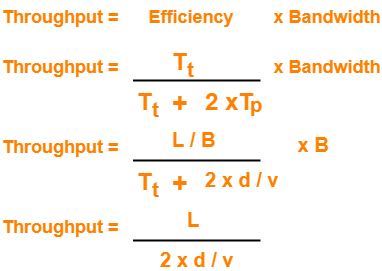
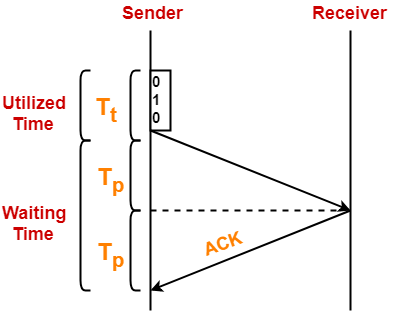
Calculating Transmission Delay-
Transmission delay (Tt)
= Frame size / Bandwidth
= 100 bytes / 20 Kbps
= (100 x 8 bits) / (20 x 103 bits per sec)
= 0.04 sec
= 40 msec
Calculating Value Of ‘a’-
a = Tp / Tt
a = 400 msec / 40 msec
a = 10
Calculating Efficiency-
Efficiency (η)
= N / (1+2a)
= 10 / (1 + 2 x 10)
= 10 / 21
= 0.476
= 47.6 %
Calculating Maximum Data Rate Possible-
Maximum data rate possible or Throughput
= Efficiency x Bandwidth
= 0.476 x 20 Kbps
= 9.52 Kbps
≅ 10 Kbps
Thus, Correct Option is (B)
Problem-02:
Consider the Go back N protocol with a sender’s window size of ‘n’. Suppose that at time ‘t’, the next inorder packet the receiver is expecting has a sequence number of ‘K’. Assume that the medium does not reorder messages.
Answer the following questions-
Part-01:
What are the possible sets of sequence numbers inside the sender’s window at time ‘t’. Assume the sender has already received the ACKs.
- [K-1, K+n-1]
- [K, K+n-1]
- [K, K+n]
- [K+n, K-1]
Part-02:
If acknowledgements are still on their way to sender, what are all possible values of the ACK field in the messages currently propagating back to the sender at a time ‘t’?
- [K-n, K-1]
- [K-1, K-n]
- [K, K-n]
- [K-n, K+1]
Solution-
Part-01:
- In Go back N protocol, the receiver window size is 1.
- It is given that receiver expects the packet having sequence number ‘K’.
- It means it has processed all the packets ranging from 0 to K-1.
- It is given that sender has received the acknowledgement for all these packets.
- So, outstanding packets in sender’s window waiting for the acknowledgement starts from K.
- Sender window size = n.
- Therefore, last packet in sender’s window will have sequence number K+n-1.
Thus, Option (B) is correct.
Part-02:
- Acknowledgement number is the next expected sequence number by the receiver.
- Receiver expects the packet having sequence number ‘K’ at time ‘t’.
- It means it has received the packets ranging from 0 to K-1 whose acknowledgements are are on the way.
- For the (K-1)th packet, acknowledgement number would be ‘K’.
- For the (K-2)th packet, acknowledgement number would be ‘K-1’ and so on.
Now,
- At any time, maximum number of outstanding packets can be ‘n’.
- This is because sender’s window size is ‘n’.
- Therefore, the possible values of acknowledgement number ranges from [K-n+1, ……, K-3, K-2, K-1, K] (total n values)
- Here, we have assumed that the acknowledgement for all the packets are sent independently.
Thus, Option (C) is correct.
Problem-03:
Station A needs to send a message consisting of 9 packets to station B using a sliding window (window size 3) and go back n error control strategy. All packets are ready and immediately available for transmission.
If every 5th packet that A transmits gets lost (but no ACKs from B ever get lost), then what is the number of packets that A will transmit for sending the message to B?
- 12
- 14
- 16
- 18
Solution-
Given-
- Total number of packets to be sent = 9
- Go back N is used where N = 3
- Every 5th packet gets lost
Step-01:
Since sender window size is 3, so sender sends 3 packets (1, 2, 3)-
![]()
Total packets sent till now from sender side = 3
Step-02:
After receiving the acknowledgement for packet-1, sender slides its window and sends packet-4.
![]()
Total packets sent till now from sender side = 4
Step-03:
After receiving the acknowledgement for packet-2, sender slides its window and sends packet-5.
![]()
Total packets sent till now from sender side = 5
Step-04:
After receiving the acknowledgement for packet-3, sender slides its window and sends packet-6.
![]()
Total packets sent till now from sender side = 6
Step-05:
After receiving the acknowledgement for packet-4, sender slides its window and sends packet-7.
![]()
Total packets sent till now from sender side = 7
Step-06:
- According to question, every 5th packet gets lost.
- So, packet-5 gets lost and when time out occurs, sender retransmits packet-5.
- In Go back N, all the following packets are also discarded by the receiver.
- So, packet-6 and packet-7 are discarded by the receiver and they are also retransmitted.
- Thus, the entire window is retransmitted.
So, we have-
![]()
Total packets sent till now from sender side = 10
Now, the next 5th packet that will be lost will be packet-7. (6, 7, 5, 6, 7)
Step-07:
After receiving the acknowledgement for packet-5, sender slides its window and sends packet-8.
![]()
Total packets sent till now from sender side = 11
Step-08:
After receiving the acknowledgement for packet-6, sender slides its window and sends packet-9.
![]()
Total packets sent till now from sender side = 12
Step-09:
- According to question, every 5th packet gets lost.
- So, packet-7 gets lost and when time out occurs, sender retransmits packet-7 and the following packets.
- Thus, the entire window is retransmitted.
So, we have-
![]()
Total packets sent till now from sender side = 15
Now, the next 5th packet that will be lost will be packet-9. (8, 9, 7, 8, 9)
Step-10:
After receiving the acknowledgement for packet-7, sender slides its window.
![]()
Total packets sent till now from sender side = 15
Step-11:
After receiving the acknowledgement for packet-8, sender slides its window.
![]()
Total packets sent till now from sender side = 15
Step-12:
- According to question, every 5th packet gets lost.
- So, packet-9 gets lost and when time out occurs, sender retransmits packet-9.
So, we have-

Total packets sent till now from sender side = 16
Finally, all the 9 packets got transmitted which took total 16 number of transmissions.
Thus, Correct Option is (C).
Problem-04:
In Go back 4, if every 6th packet that is being transmitted is lost and if total number of packets to be sent is 10, then how many transmissions will be required?
Solution-
- Try yourself!
- We have to solve in exactly the same way as we have solved Problem-03.
- Total number of transmissions required will be 17.
Problem-05:
A 1 Mbps satellite link connects two ground stations. The altitude of the satellite is 36504 km and speed of the signal is 3 x 108 m/sec. What should be the packet size for a channel utilization of 25% for a satellite link using go back 127 sliding window protocol?
- 120 bytes
- 60 bytes
- 240 bytes
- 90 bytes
Solution-
Given-
- Bandwidth = 1 Mbps
- Distance = 2 x 36504 km = 73008 km
- Propagation speed = 3 x 108 m/sec
- Efficiency = 25% = 1/4
- Go back N is used where N = 127
Let the packet size be L bits.
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= L bits / 1 Mbps
= L μsec
Calculating Propagation Delay-
Propagation delay (Tp)
= Distance / Speed
= (73008 x 103 m) / (3 x 108 m/sec)
= 24336 x 10-5 sec
= 243360 μsec
Calculating Value of ‘a’-
a = Tp / Tt
a = 243360 μsec / L μsec
a = 243360 / L
Calculating Packet Size-
Efficiency (η) = N / (1+2a)
Substituting the values, we get-
1/4 = 127 / (1 + 2 x 243360 / L)
1/4 = 127 x L / (L + 486720)
L + 486720 = 508 x L
507 x L = 486720
L = 960
From here, packet size = 960 bits or 120 bytes.
Thus, Correct Option is (A).
Problem-06:
Consider a network connecting two systems located 8000 km apart. The bandwidth of the network is 500 x 106 bits per second. The propagation speed of the media is 4 x 106 meters per second. It is needed to design a Go back N sliding window protocol for this network. The average packet size is 107 bits. The network is to be used to its full capacity.
Assume that processing delays at nodes are negligible. Then, the minimum size in bits of the sequence number field has to be ______ ?
Solution-
Given-
- Distance = 8000 km
- Bandwidth = 500 x 106 bps
- Propagation speed = 4 x 106 m/sec
- Packet size = 107 bits
Now,
- For using the network to its full capacity, Efficiency (η) = 1
- Efficiency (η) = 1 when sender window size = 1+2a
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= 107 bits / (500 x 106 bits per sec)
= 1 / 50 sec
= 0.02 sec
Calculating Propagation Delay-
Propagation delay (Tp)
= Distance / Speed
= 8000 km / (4 x 106 m/sec)
= 2 sec
Calculating Value of ‘a’-
a = Tp / Tt
a = 2 sec / 0.02 sec
a = 100
Calculating Sender Window Size-
Sender window size
= 1 + 2a
= 1 + 2 x 100
= 201
Calculating Minimum Size Of Sequence Number Field-
Minimum number of bits required in the sequence number field
= ⌈log2(1+2a)⌉
= ⌈log2(201)⌉
= ⌈7.65⌉
= 8
Thus, Minimum size of sequence number field = 8 bits.
Next Article- Selective Repeat Protocol
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.