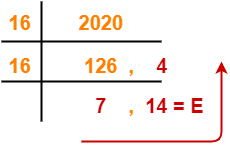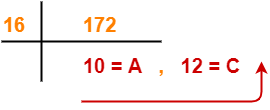Tag: Number System Conversion Questions and Answers PDF

Converting Bases | Conversion of Bases

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from any base to any other base.

 

 

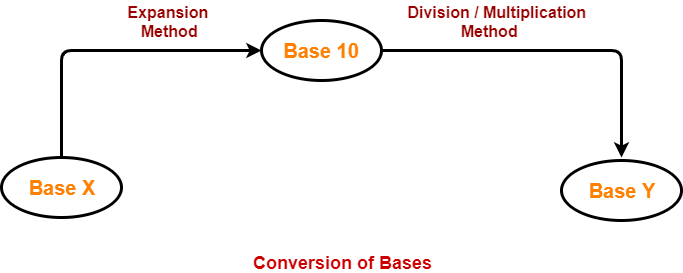
Conversion of Bases-

 

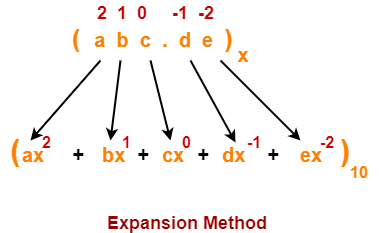
A given number in base x can be converted to any other base y using the following steps-

 

Step-01:

 

Convert the number from base x to base 10 using expansion method.

 

Read More- Conversion to Base 10

 

Step-02:

 

Convert the number from base 10 to base y using division & multiplication method.

 

 

Read More-

 

PRACTICE PROBLEMS BASED ON CONVERSION OF BASES-

 

Problem-01:

 

Convert (1056)16 to ( ? )8

 

Solution-

 

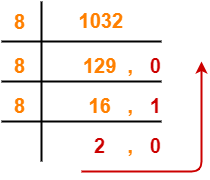
Step-01: Conversion To Base 10-

 

(1056)16 → ( ? )10

 

Using Expansion method, we have-

(1056)16

= 1 x 163 + 0 x 162 + 5 x 161 + 6 x 160

= 4096 + 0 + 80 + 6

= (4182)10

 

From here, (1056)16 = (4182)10

 

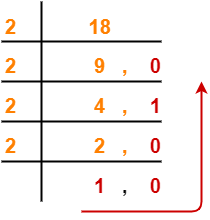
Step-02: Conversion To Base 8-

 

(4182)10 → ( ? )8

 

Using Division method, we have-

 

 

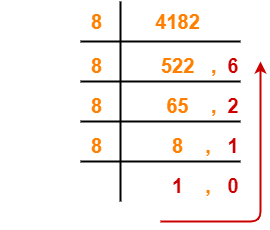
From here, (4182)10 = (10126)8

Thus, (1056)16 = (10126)8

 

Also Read- http://www.exam-labs.com

 

Problem-02:

 

Convert (11672)8 to ( ? )16

 

Solution-

 

Step-01: Conversion To Base 10-

 

(11672)8 → ( ? )10

 

Using Expansion method, we have-

(11672)8

= 1 x 84 + 1 x 83 + 6 x 82 + 7 x 81 + 2 x 80

= 4096 + 512 + 384 + 56 + 2

= (5050)10

 

From here, (11672)8 = (5050)10

 

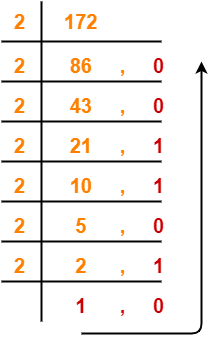
Step-02: Conversion To Base 16-

 

(5050)10 → ( ? )16

 

Using Division method, we have-

 

 

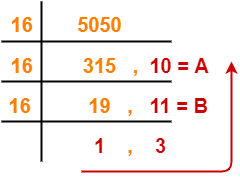
From here, (5050)10 = (13BA)16

Thus, (11672)8 = (13BA)16

 

Problem-03:

 

Convert (2724)8 to ( ? )5

 

Solution-

 

Step-01: Conversion To Base 10-

 

(2724)8 → ( ? )10

 

Using Expansion method, we have-

(2724)8

= 2 x 83 + 7 x 82 + 2 x 81 + 4 x 80

= 1024 + 448 + 16 + 4

= (1492)10

 

From here, (2724)8 = (1492)10

 

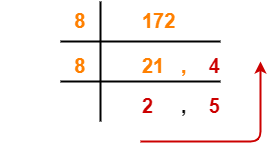
Step-02: Conversion To Base 5-

 

(1492)10 → ( ? )5

 

Using Division method, we have-

 

 

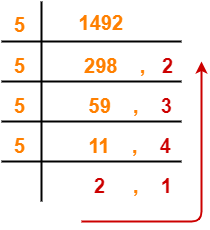
From here, (1492)10 = (21432)5

Thus, (2724)8 = (21432)5

 

Problem-04:

 

Convert (3211)4 to ( ? )5

 

Solution-

 

Step-01: Conversion To Base 10-

 

(3211)4 → ( ? )10

 

Using Expansion method, we have-

(3211)4

= 3 x 43 + 2 x 42 + 1 x 41 + 1 x 40

= 192 + 32 + 4 + 1

= (229)10

 

From here, (3211)4 = (229)10

 

Step-02: Conversion To Base 5-

 

(229)10 → ( ? )5

 

Using Division method, we have-

 

 

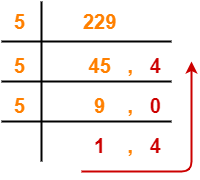
From here, (229)10 = (1404)5

Thus, (3211)4 = (1404)5

 

Problem-05:

 

Convert (1001001100)2 to ( ? )6

 

Solution-

 

Step-01: Conversion To Base 10-

 

(1001001100)2 → ( ? )10

 

Using Expansion method, we have-

(1001001100)2

= 1 x 29 + 0 x 28 + 0 x 27 + 1 x 26 + 0 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 0 x 20

= 512 + 64 + 8 + 4

= (588)10

 

From here, (1001001100)2 = (588)10

 

Step-02: Conversion To Base 6-

 

(588)10 → ( ? )6

 

Using Division method, we have-

 

 

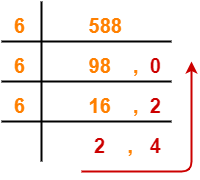
From here, (588)10 = (2420)6

Thus, (1001001100)2 = (2420)6

 

To gain better understanding about Conversion of Bases,

Watch this Video Lecture

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Decimal to Hexadecimal | Base 10 to base 16

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from base 10 to base 16.

 

 

Decimal to Hexadecimal Conversion-

 

A given number can be converted from base 10 to any other base using division method and multiplication method.

 

Following two cases are possible-

 

Case-01: For Numbers Carrying No Fractional Part-

 

  • Division Method is used to convert such numbers from base 10 to another base.
  • The division is performed with the required base.

 

Steps To Convert From Base 10 to Base 16-

 

  • Divide the given number (in base 10) with 16 until the result finally left is less than 16.
  • Traverse the remainders from bottom to top to get the required number in base 16.

 

Case-02: For Numbers Carrying A Fractional Part-

 

To convert such numbers from base 10 to another base, real part and fractional part are treated separately.

 

For Real Part-

 

The steps involved in converting the real part from base 10 to another base are same as above.

 

For Fractional Part-

 

  • Multiplication Method is used to convert fractional part from base 10 to another base.
  • The multiplication is performed with the required base.

 

Steps To Convert From Base 10 To Base 16-

 

  • Multiply the given fraction (in base 10) with 16.
  • Write the real part and fractional part of the result so obtained separately.
  • Multiply the fractional part with 16.
  • Write the real part and fractional part of the result so obtained separately.
  • Repeat this procedure until the fractional part remains 0.
  • If fractional part does not terminate to 0, find the result up to as many places as required.

 

Required Number in Base 16

= Series of real part of multiplication results obtained in the above steps from top to bottom

 

Also Read- Conversion to Base 10

 

PRACTICE PROBLEMS BASED ON DECIMAL TO HEXADECIMAL CONVERSION-

 

Problems-

 

Convert the following numbers from base 10 to base 16-

  1. (2020)10
  2. (2020.65625)10
  3. (172)10
  4. (172.983)10

 

Solution-

 

1. (2020)10

 

(2020)10 → (?)16

 

Using division method, we have-

 

 

From here, (2020)10 = (7E4)16

 

2. (2020.65625)10

 

(2020.65625)10 → ( ? )8

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (2020)10
  • We convert the real part from base 10 to base 16 using division method same as above.

 

So, (2020)10 = (7E4)16

 

For Fractional Part-

 

  • The fractional part is (0.65625)10
  • We convert the fractional part from base 10 to base 16 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.65625 x 16 10 = A 0.5
0.5 x 16 8 0.0

 

Explanation

 

Step-01:

 

  • Multiply 0.65625 with 16. Result = 10.5.
  • Write 10 (= A in hexadecimal) in real part and 0.5 in fractional part.

 

Step-02:

 

  • Multiply 0.5 with 16. Result = 8.0.
  • Write 8 in real part and 0.0 in fractional part.

 

Since fractional part becomes 0, so we stop.

 

  • The fractional part terminates to 0 after 2 iterations.
  • Traverse the real part column from top to bottom to obtain the required number in base 16.

 

From here, (0.65625)10 = (0.A8)8

 

Combining the result of real and fractional parts, we have-

(2020.65625)10 = (7E4.A8)16

 

3. (172)10

 

(172)10 → ( ? )16

 

Using division method, we have-

 

 

From here, (172)10 = (AC)16

 

4. (172.983)10

 

(172.983)10 → ( ? )16

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (172)10
  • We convert the real part from base 10 to base 16 using division method same as above.

 

So, (172)10 = (AC)16

 

For Fractional Part-

 

  • The fractional part is (0.983)10
  • We convert the fractional part from base 10 to base 16 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.983 x 16 15 = F 0.728
0.728 x 16 11 = B 0.648
0.648 x 16 10 = A 0.368
0.368 x 16 5 0.888

 

  • The fractional part does not terminates to 0 after several iterations.
  • So, let us find the value up to 4 decimal places.
  • Traverse the real part column from top to bottom to obtain the required number in base 16.

 

From here, (0.983)10 = (0.FBA5)8

 

Combining the result of real and fractional parts, we have-

(172.983)10 = (AC.FBA5)16

 

Also Read- Decimal to Octal Conversion

 

To gain better understanding about Decimal to Hexadecimal Conversion,

Watch this Video Lecture

 

Next Article- Converting Any Base To Any Base

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Decimal to Octal Conversion | Base 10 to Base 8

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from base 10 to base 8.

 

 

Decimal to Octal Conversion-

 

A given number can be converted from base 10 to any other base using division method and multiplication method.

 

Following two cases are possible-

 

Case-01: For Numbers Carrying No Fractional Part-

 

  • Division Method is used to convert such numbers from base 10 to another base.
  • The division is performed with the required base.

 

Steps To Convert From Base 10 to Base 8-

 

  • Divide the given number (in base 10) with 8 until the result finally left is less than 8.
  • Traverse the remainders from bottom to top to get the required number in base 8.

 

Case-02: For Numbers Carrying A Fractional Part-

 

To convert such numbers from base 10 to another base, real part and fractional part are treated separately.

 

For Real Part-

 

The steps involved in converting the real part from base 10 to another base are same as above.

 

For Fractional Part-

 

  • Multiplication Method is used to convert fractional part from base 10 to another base.
  • The multiplication is performed with the required base.

 

Steps To Convert From Base 10 To Base 8-

 

  • Multiply the given fraction (in base 10) with 8.
  • Write the real part and fractional part of the result so obtained separately.
  • Multiply the fractional part with 8.
  • Write the real part and fractional part of the result so obtained separately.
  • Repeat this procedure until the fractional part remains 0.
  • If fractional part does not terminate to 0, find the result up to as many places as required.

 

Required Number in Base 8

= Series of real part of multiplication results obtained in the above steps from top to bottom

 

Also Read- Conversion to Base 10

 

PRACTICE PROBLEMS BASED ON DECIMAL TO OCTAL CONVERSION-

 

Problems-

 

Convert the following numbers from base 10 to base 8-

  1. (1032)10
  2. (1032.6875)10
  3. (172)10
  4. (172.878)10

 

Solution-

 

1. (1032)10

 

(1032)10 → (?)8

 

Using division method, we have-

 

 

From here, (1032)10 = (2010)8

 

2. (1032.6875)10

 

(1032.6875)10 → ( ? )8

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (1032)10
  • We convert the real part from base 10 to base 8 using division method same as above.

 

So, (1032)10 = (2010)8

 

For Fractional Part-

 

  • The fractional part is (0.6875)10
  • We convert the fractional part from base 10 to base 8 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.6875 x 8 5 0.5
0.5 x 8 4 0.0

 

Explanation

 

Step-01:

 

  • Multiply 0.6875 with 8. Result = 5.5.
  • Write 5 in real part and 0.5 in fractional part.

 

Step-02:

 

  • Multiply 0.5 with 8. Result = 4.0.
  • Write 4 in real part and 0.0 in fractional part.

 

Since fractional part becomes 0, so we stop.

 

  • The fractional part terminates to 0 after 2 iterations.
  • Traverse the real part column from top to bottom to obtain the required number in base 8.

 

From here, (0.6875)10 = (0.54)8

 

Combining the result of real and fractional parts, we have-

(1032.6875)10 = (2010.54)8

 

3. (172)10

 

(172)10 → ( ? )8

 

Using division method, we have-

 

 

From here, (172)10 = (254)8

 

4. (172.878)10

 

(172.878)10 → ( ? )8

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (172)10
  • We convert the real part from base 10 to base 8 using division method same as above.

 

So, (172)10 = (254)8

 

For Fractional Part-

 

  • The fractional part is (0.878)10
  • We convert the fractional part from base 10 to base 8 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.878 x 8 7 0.024
0.024 x 8 0 0.192
0.192 x 8 1 0.536
0.536 x 8 4 0.288

 

  • The fractional part does not terminates to 0 after several iterations.
  • So, let us find the value up to 4 decimal places.
  • Traverse the real part column from top to bottom to obtain the required number in base 8.

 

From here, (0.878)10 = (0.7014)8

 

Combining the result of real and fractional parts, we have-

(172.878)10 = (254.7014)8

 

Also Read- Decimal to Binary Conversion

 

To gain better understanding about Decimal to Octal Conversion,

Watch this Video Lecture

 

Next Article- Decimal to Hexadecimal Conversion

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Decimal to Binary Conversion | Base 10 to base 2

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from base 10 to base 2.

 

 

Decimal to Binary Conversion-

 

A given number can be converted from base 10 to any other base using division method and multiplication method.

 

Learn how much goods and services should cost from painting a car or reupholstering a car windshield

to hiring wedding planner or a cook at The Pricer.

 

Following two cases are possible-

 

Case-01: For Numbers Carrying No Fractional Part-

 

  • Division Method is used to convert such numbers from base 10 to another base.
  • The division is performed with the required base.

 

Steps To Convert From Base 10 to Base 2-

 

  • Divide the given number (in base 10) with 2 until the result finally left is less than 2.
  • Traverse the remainders from bottom to top to get the required number in base 2.

 

Case-02: For Numbers Carrying A Fractional Part-

 

To convert such numbers from base 10 to another base, real part and fractional part are treated separately.

 

For Real Part-

 

The steps involved in converting the real part from base 10 to another base are same as above.

 

For Fractional Part-

 

  • Multiplication Method is used to convert fractional part from base 10 to another base.
  • The multiplication is performed with the required base.

 

Steps To Convert From Base 10 To Base 2-

 

  • Multiply the given fraction (in base 10) with 2.
  • Write the real part and fractional part of the result so obtained separately.
  • Multiply the fractional part with 2.
  • Write the real part and fractional part of the result so obtained separately.
  • Repeat this procedure until the fractional part remains 0.
  • If fractional part does not terminate to 0, find the result up to as many places as required.

 

Required Number in Base 2

= Series of real part of multiplication results obtained in the above steps from top to bottom

 

Also Read- Conversion to Base 10

 

PRACTICE PROBLEMS BASED ON DECIMAL TO BINARY CONVERSION-

 

Problems-

 

Convert the following numbers from base 10 to base 2-

  1. (18)10
  2. (18.625)10
  3. (172)10
  4. (172.878)10

 

Solution-

 

1. (18)10

 

(18)10 → ( ? )2

 

Using division method, we have-

 

 

From here, (18)10 = (10010)2

 

2. (18.625)10

 

(18.625)10 → ( ? )2

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (18)10
  • We convert the real part from base 10 to base 2 using division method same as above.

 

So, (18)10 = (10010)2

 

For Fractional Part-

 

  • The fractional part is (0.625)10
  • We convert the fractional part from base 10 to base 2 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.625 x 2 1 0.25
0.25 x 2 0 0.50
0.50 x 2 1 0

 

Explanation

 

Step-01:

 

  • Multiply 0.625 with 2. Result = 1.25.
  • Write 1 in real part and 0.25 in fractional part.

 

Step-02:

 

  • Multiply 0.25 with 2. Result = 0.50.
  • Write 0 in real part and 0.50 in fractional part.

 

Step-03:

 

  • Multiply 0.50 with 2. Result = 1.0.
  • Write 1 in real part and 0.0 in fractional part.

 

Since fractional part becomes 0, so we stop.

 

  • The fractional part terminates to 0 after 3 iterations.
  • Traverse the real part column from top to bottom to obtain the required number in base 2.

 

From here, (0.625)10 = (0.101)2

 

Combining the results of real part and fractional part, we have-

(18.625)10 = (10010.101)2

 

3. (172)10

 

(172)10 → ( ? )2

 

Using division method, we have-

 

 

From here, (172)10 = (10101100)2

 

4. (172.878)10

 

(172.878)10 → ( ? )2

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (172)10
  • We convert the real part from base 10 to base 2 using division method same as above.

 

So, (172)10 = (10101100)2

 

For Fractional Part-

 

  • The fractional part is (0.878)10
  • We convert the fractional part from base 10 to base 2 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.878 x 2 1 0.756
0.756 x 2 1 0.512
0.512 x 2 1 0.024
0.024 x 2 0 0.048

 

  • The fractional part does not terminates to 0 after several iterations.
  • So, let us find the value up to 4 decimal places.
  • Traverse the real part column from top to bottom to obtain the required number in base 2.

 

From here, (0.878)10 = (0.1110)2

 

Combining the results of real part and fractional part, we have-

(172.878)10 = (10101100.1110)2

 

To gain better understanding about Decimal to Binary Conversion,

Watch this Video Lecture

 

Next Article- Decimal to Octal Conversion

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Convert to Base 10 | Number System Conversions

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from any base to base 10.

 

 

Converting to Base 10-

 

A given number can be converted from any base to base 10 using Expansion Method.

According to expansion method, if abc.de is any given number in base x, then its value in base 10 is given as-

 

(abc.de)x = (ax2 + bx + c + dx-1 + ex-2)10

 

Explanation-

 

To use expansion method for conversion,

  • Assign position number to each digit of the given number.
  • Digits to the left of decimal are numbered starting from 0.
  • Digits to the right of decimal are numbered starting from -1.
  • Write a term for each digit as digit x (base of given number)position number of digit
  • Perform the addition of all terms to obtain the number in base 10.
  • This formula can be expanded for any number of digits.

 

 

PRACTICE PROBLEMS BASED ON CONVERSION TO BASE 10-

 

Convert the following numbers to base 10-

  1. (10010)2
  2. (254)8
  3. (AC)16
  4. (10010.101)2
  5. (254.7014)8
  6. (AC.FBA5)16
  7. (0.1402)8
  8. (0.ABDF)16

 

Solutions-

 

1. (10010)2

 

(10010)2 → ( ? )10

 

Using expansion method, we have-

(10010)2

= ( 1 x 24 + 0 x 23 + 0 x 22 + 1 x 21 + 0 x 20 )10

= ( 16 + 0 + 0 + 2 + 0 )10

= ( 18 )10

 

2. (254)8

 

(254)8 → ( ? )10

 

Using expansion method, we have-

(254)8

= ( 2 x 82 + 5 x 81 + 4 x 80 )10

= ( 128 + 40 + 4 )10

= ( 172 )10

 

3. (AC)16

 

(AC)16 → ( ? )10

 

Using expansion method, we have-

(AC)16

= ( A x 161 + C x 160 )10

= ( 10 x 16 + 12 x 1 )10

= ( 160 + 12 )10

= ( 172 )10

 

4. (10010.101)2

 

(10010.101)2 → ( ? )10

 

Using expansion method, we have-

(10010.101)2

= ( 1 x 24 + 0 x 23 + 0 x 22 + 1 x 21 + 0 x 20 + 1 x 2-1 + 0 x 2-2 + 1 x 2-3 )10

= ( 16 + 0 + 0 + 2 + 0 + 0.5 + 0.125 )10

= ( 18.625 )10

 

5. (254.7014)8

 

(254.7014)8 → ( ? )10

 

Using expansion method, we have-

(254.7014)8

= ( 2 x 82 + 5 x 81 + 4 x 80 + 7 x 8-1 + 0 x 8-2 + 1 x 8-3 + 4 x 8-4 )10

= ( 128 + 40 + 4 + 0.875 + 0.0019 + 0.0009 )10

= ( 172.8778 )10

 

6. (AC.FBA5)16

 

(AC.FBA5)16 → ( ? )10

 

Using expansion method, we have-

(AC.FBA5)16

= ( A x 161 + C x 160 + F x 16-1 + B x 16-2 + A x 16-3 + 5 x 16-4 )10

= ( 10 x 16 + 12 x 1 + 15 x 16-1 + 11 x 16-2 + 10 x 16-3 + 5 x 16-4 )10

= ( 160 + 12 + 0.9375 + 0.0429 + 0.0024 + 0.0001 )10

= ( 172.9829 )10

 

7. (0.1402)8

 

(0.1402)8 → ( ? )10

 

Using expansion method, we have-

(0.1402)8

= ( 0 x 80 + 1 x 8-1 + 4 x 8-2 + 0 x 8-3 + 2 x 8-4 )10

= ( 0 + 0.125 + 0.0625 + 0 + 0.0005 )10

= ( 0.188 )10

 

8. (0.ABDF)16

 

(0.ABDF)16 → ( ? )10

 

Using expansion method, we have-

(0.ABDF)16

= ( 0 x 160 + A x 16-1 + B x 16-2 + D x 16-3 + F x 16-4 )10

= ( 0 x 1 + 10 x 16-1 + 11 x 16-2 + 13 x 16-3 + 15 x 16-4 )10

= ( 0 + 0.625 + 0.0429 + 0.0032 + 0.0002 )10

= ( 0.6713 )10

 

To gain better understanding about Conversion to Base 10,

Watch this Video Lecture

 

Next Article- Decimal to Binary Conversion

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.