Memory Management | Gate Vidyalay

Tag: Memory Management

Page Replacement Algorithms | Page Fault

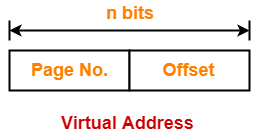
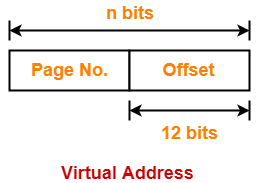
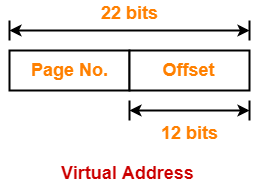
Page Fault in OS-

Before you go through this article, make sure that you have gone through the previous article on Page Fault in OS.

We have discussed-

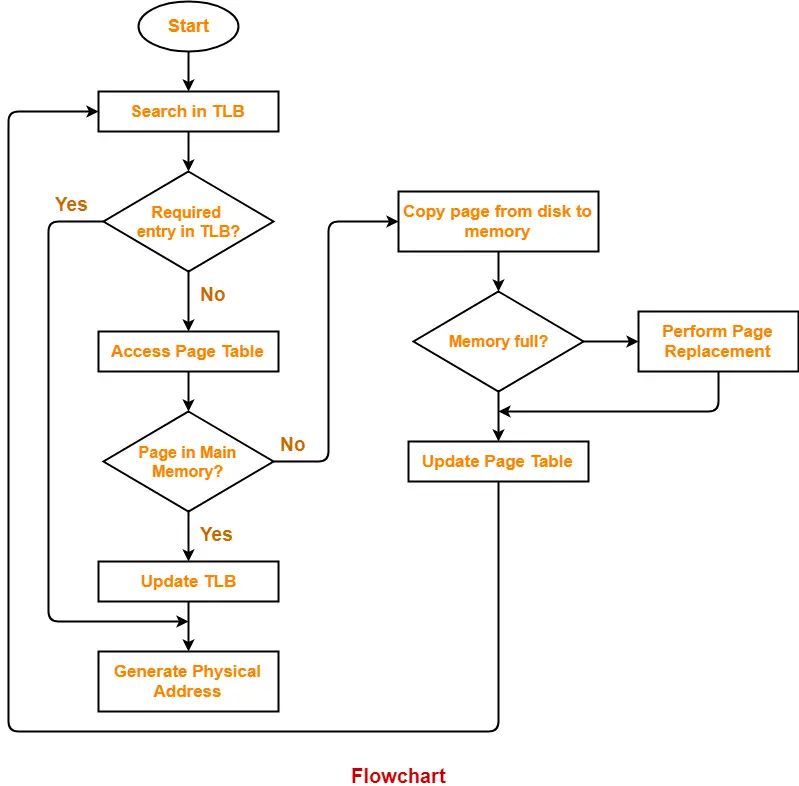
A page fault occurs when a page referenced by the CPU is not found in the main memory.
The required page has to be brought from the secondary memory into the main memory.
A page has to be replaced if all the frames of main memory are already occupied.

Page Replacement-

Page replacement is a process of swapping out an existing page from the frame of a main memory and replacing it with the required page.

Page replacement is required when-

All the frames of main memory are already occupied.
Thus, a page has to be replaced to create a room for the required page.

Page Replacement Algorithms-

Page replacement algorithms help to decide which page must be swapped out from the main memory to create a room for the incoming page.

Various page replacement algorithms are-

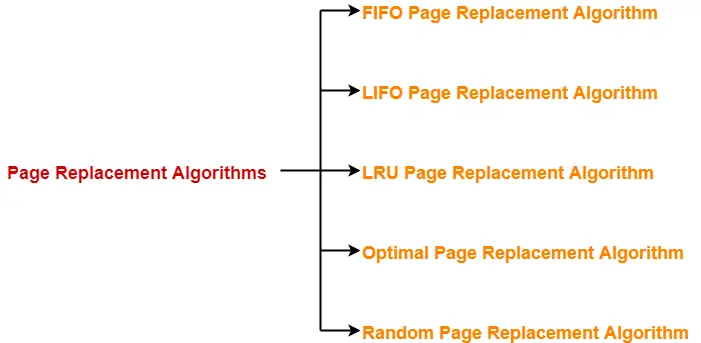
FIFO Page Replacement Algorithm
LIFO Page Replacement Algorithm
LRU Page Replacement Algorithm
Optimal Page Replacement Algorithm
Random Page Replacement Algorithm

A good page replacement algorithm is one that minimizes the number of page faults.

FIFO Page Replacement Algorithm-

As the name suggests, this algorithm works on the principle of “First in First out“.
It replaces the oldest page that has been present in the main memory for the longest time.
It is implemented by keeping track of all the pages in a queue.

LIFO Page Replacement Algorithm-

As the name suggests, this algorithm works on the principle of “Last in First out“.
It replaces the newest page that arrived at last in the main memory.
It is implemented by keeping track of all the pages in a stack.

NOTE

Only frame is used for page replacement during entire procedure after all the frames get occupied.

LRU Page Replacement Algorithm-

As the name suggests, this algorithm works on the principle of “Least Recently Used“.
It replaces the page that has not been referred by the CPU for the longest time.

Optimal Page Replacement Algorithm-

This algorithm replaces the page that will not be referred by the CPU in future for the longest time.
It is practically impossible to implement this algorithm.
This is because the pages that will not be used in future for the longest time can not be predicted.
However, it is the best known algorithm and gives the least number of page faults.
Hence, it is used as a performance measure criterion for other algorithms.

Random Page Replacement Algorithm-

As the name suggests, this algorithm randomly replaces any page.
So, this algorithm may behave like any other algorithm like FIFO, LIFO, LRU, Optimal etc.

PRACTICE PROBLEMS BASED ON PAGE REPLACEMENT ALGORITHMS-

Problem-01:

A system uses 3 page frames for storing process pages in main memory. It uses the First in First out (FIFO) page replacement policy. Assume that all the page frames are initially empty. What is the total number of page faults that will occur while processing the page reference string given below-

4 , 7, 6, 1, 7, 6, 1, 2, 7, 2

Also calculate the hit ratio and miss ratio.

Solution-

Total number of references = 10

From here,

Total number of page faults occurred = 6

Calculating Hit ratio-

Total number of page hits

= Total number of references – Total number of page misses or page faults

= 10 – 6

= 4

Thus, Hit ratio

= Total number of page hits / Total number of references

= 4 / 10

= 0.4 or 40%

Calculating Miss ratio-

Total number of page misses or page faults = 6

Thus, Miss ratio

= Total number of page misses / Total number of references

= 6 / 10

= 0.6 or 60%

Alternatively,

Miss ratio

= 1 – Hit ratio

= 1 – 0.4

= 0.6 or 60%

Problem-02:

A system uses 3 page frames for storing process pages in main memory. It uses the Least Recently Used (LRU) page replacement policy. Assume that all the page frames are initially empty. What is the total number of page faults that will occur while processing the page reference string given below-

4 , 7, 6, 1, 7, 6, 1, 2, 7, 2

Also calculate the hit ratio and miss ratio.

Solution-

Total number of references = 10

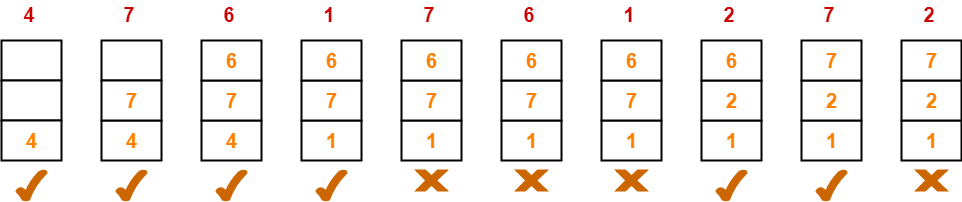
From here,

Total number of page faults occurred = 6

In the similar manner as above-

Hit ratio = 0.4 or 40%
Miss ratio = 0.6 or 60%

Problem-03:

A system uses 3 page frames for storing process pages in main memory. It uses the Optimal page replacement policy. Assume that all the page frames are initially empty. What is the total number of page faults that will occur while processing the page reference string given below-

4 , 7, 6, 1, 7, 6, 1, 2, 7, 2

Also calculate the hit ratio and miss ratio.

Solution-

Total number of references = 10

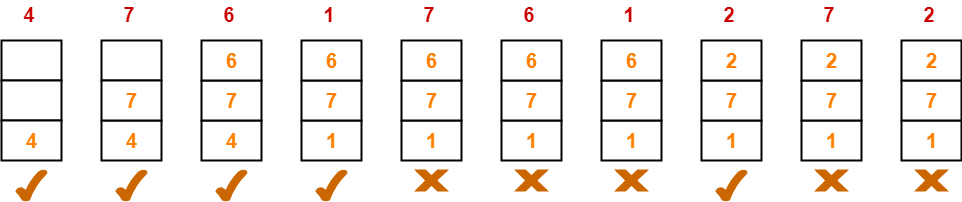
From here,

Total number of page faults occurred = 5

In the similar manner as above-

Hit ratio = 0.5 or 50%
Miss ratio = 0.5 or 50%

To gain better understanding about Page Replacement Algorithms,

Watch this Video Lecture

Next Article- Practice Problems On Page Fault

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Page Fault | Paging | Practice Problems

Operating System

Page Fault in OS-

Before you go through this article, make sure that you have gone through the previous article on Page Fault in OS.

We have discussed-

A page fault occurs when the referenced page is not found in the main memory.
Page fault handling routine is executed on the occurrence of page fault.
The time taken to service the page fault is called as page fault service time.

Effective Access time-

In a multilevel paging scheme using TLB without any possibility of page fault, effective access time is given by-

In a multilevel paging scheme using TLB with a possibility of page fault, effective access time is given by-

Also Read- Page Replacement Algorithms

PRACTICE PROBLEMS BASED ON PAGE FAULTS IN OS-

Problem-01:

Let the page fault service time be 10 ms in a computer with average memory access time being 20 ns. If one page fault is generated for every 10⁶ memory accesses, what is the effective access time for the memory?

21 ns
30 ns
23 ns
35 ns

Solution-

Given-

Page fault service time = 10 ms
Average memory access time = 20 ns
One page fault occurs for every 10⁶ memory accesses

Page Fault Rate-

It is given that one page fault occurs for every 10⁶ memory accesses.

Thus,

Page fault rate

= 1 / 10⁶

= 10^-6

Effective Access Time With Page Fault-

It is given that effective memory access time without page fault = 20 ns.

Now, substituting values in the above formula, we get-

Effective access time with page fault

= 10^-6 x { 20 ns + 10 ms } + ( 1 – 10^-6 ) x { 20 ns }

= 10^-6 x 10 ms + 20 ns

= 10^-5 ms + 20 ns

= 10 ns + 20 ns

= 30 ns

Thus, Option (B) is correct.

Problem-02:

Suppose the time to service a page fault is on the average 10 milliseconds, while a memory access takes 1 microsecond. Then, a 99.99% hit ratio results in average memory access time of-

1.9999 milliseconds
1 millisecond
9.999 microseconds
1.9999 microseconds
None of these

Solution-

Given-

Page fault service time = 10 msec
Average memory access time = 1 μsec
Hit ratio = 99.99% = 0.9999

Page Fault Rate-

Page fault rate

= 1 – Hit ratio

= 1 – 0.9999

= 0.0001

Effective Access Time With Page Fault-

It is given that effective memory access time without page fault = 1 μsec.

Substituting values in the above formula, we get-

Effective access time with page fault

= 0.0001 x { 1 μsec + 10 msec } + 0.99999 x 1 μsec

= 0.0001 μsec + 0.001 msec + 0.9999 μsec

= 1 μsec + 0.001 msec

= 1 μsec + 1 μsec

= 2 μsec or 0.002 msec

Thus, Option (E) is correct.

Problem-03:

If an instruction takes i microseconds and a page fault takes an additional j microseconds, the effective instruction time if on the average a page fault occurs every k instruction is-

i + j / k
i + j x k
(i + j) / k
(i + j) x k

Solution-

Given-

Page fault service time = j μsec
Average memory access time = i μsec
One page fault occurs every k instruction

Page Fault Rate-

It is given that one page fault occurs every k instruction.

Thus,

Page fault rate

= 1 / k

Effective Access Time With Page Fault-

It is given that effective memory access time without page fault = i μsec

Now, substituting values in the above formula, we get-

Effective access time with page fault

= (1 / k) x { i μsec + j μsec } + ( 1 – 1 / k) x { i μsec }

= j / k μsec + i μsec

= i + j / k μsec

Thus, Option (A) is correct.

Problem-04:

Consider a system with a two-level paging scheme in which a regular memory access takes 150 nanoseconds and servicing a page fault takes 8 milliseconds. An average instruction takes 100 nanoseconds of CPU time and two memory accesses. The TLB hit ratio is 90% and the page fault rate is one in every 10,000 instructions. What is the effective average instruction execution time?

645 nanoseconds
1050 nanoseconds
1215 nanoseconds
1230 nanoseconds
None of these

Solution-

Given-

Number of levels of page table = 2
Main memory access time = 150 ns
Page fault service time = 8 msec
Average instruction takes 100 ns of CPU time and 2 memory accesses
TLB Hit ratio = 90% = 0.9
Page fault rate = 1 / 10⁴ = 10^-4

Assume TLB access time = 0 since it is not given in the question.

Also, TLB access time is much less as compared to the memory access time.

Effective Access Time Without Page Fault-

Substituting values in the above formula, we get-

Effective memory access time without page fault

= 0.9 x { 0 + 150 ns } + 0.1 x { 0 + (2+1) x 150 ns }

= { 0.9 x 150 ns } + { 0.1 x 450 ns }

= 135 ns + 45 ns

= 180 ns

Effective Access Time With Page Fault-

Substituting values in the above formula, we get-

Effective access time with page fault

= 10^-4 x { 180 ns + 8 msec } + (1 – 10^-4) x 180 ns

= 8 x 10^-4 msec + 180 ns

= 8 x 10^-7 sec + 180 ns

= 800 ns + 180 ns

= 980 ns

Effective Average Instruction Execution Time-

Effective Average Instruction Execution Time

= 100 ns + 2 x Effective memory access time with page fault

= 100 ns + 2 x 980 ns

= 100 ns + 1960 ns

= 2060 ns

Thus, Option (E) is correct.

Problem-05:

A demand paging system takes 100 time units to service a page fault and 300 time units to replace a dirty page. Memory access time is 1 time unit. The probability of a page fault is p. In case of a page fault, the probability of page being dirty is also p. It is observed that the average access time is 3 time units. Then the value of p is-

0.194
0.233
0.514
0.981
None of these

Solution-

Given-

Page fault service time = 100 time units
Time taken to replace dirty page = 300 time units
Average memory access time = 1 time unit
Page fault rate = p
Probability of page being dirty = p
Effective access time = 3 time units

Now, According to question-

3 time units = p x { 1 time unit + p x { 300 time units } + (1 – p) x { 100 time units } } + (1 – p) x { 1 time unit }

3 = p x { 1 + 300p + 100 – 100p } + (1 – p)

3 = p x { 101 + 200p } + (1 – p)

3 = 101p + 200p² + 1 – p

3 = 100p + 200p² + 1

200p² + 100p – 2 = 0

On solving this quadratic equation, we get p = 0.019258

Thus, Option (E) is correct.

Next Article- Belady’s Anomaly

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Page Fault | Page Replacement Algorithms

Operating System

Paging in OS-

Before you go through this article, make sure that you have gone through the previous article on Paging in OS.

We have discussed-

Paging is a non-contiguous memory allocation technique.
In a paging scheme, a process is divided into several pages.
The pages are then stored in different frames of the main memory.

Page Fault-

When a page referenced by the CPU is not found in the main memory, it is called as a page fault.
When a page fault occurs, the required page has to be fetched from the secondary memory into the main memory.

Translating Logical Address into Physical Address-

In a paging scheme using TLB with possibility of page fault,

The logical address generated by the CPU is translated into the physical address using the following steps-

Step-01:

CPU generates a logical address consisting of two parts-

Page Number
Page Offset

Step-02:

TLB is checked to see if it contains an entry for the referenced page number.
The referenced page number is compared with the TLB entries all at once.

Now, two cases are possible-

Case-01: If there is a TLB hit-

If TLB contains an entry for the referenced page number, a TLB hit occurs.
In this case, TLB entry is used to get the frame number for the referenced page number.

Case-02: If there is a TLB miss-

If TLB does not contain an entry for the referenced page number, a TLB miss occurs.
In this case, page table is used to get the frame number for the referenced page number.
The valid / invalid bit of the page table entry indicates whether the referenced page is present in the main memory or not.

Also read- Page Table Entries

Now, two cases are possible-

Case-01: If Valid / Invalid Bit is Set to 1-

If valid / invalid bit is set to 1, it indicates that the page is present in the main memory.
Then, page table is used to get the frame number for the referenced page number.
Then, TLB is updated with the page number and its frame number for future references.

Case-02: If Valid / Invalid Bit is Set to 0-

If valid / invalid bit is set to 0, it indicates that the page is not present in the main memory.
A page fault occurs.
The occurrence of page fault calls the page fault interrupt which executes the page fault handling routine.

Page Fault Handling Routine-

The following sequence of events take place-

The currently running process is stopped and context switching occurs.
The referenced page is copied from the secondary memory to the main memory.
If the main memory is already full, a page is replaced to create a room for the referenced page.
After copying the referenced page successfully in the main memory, the page table is updated.
When the execution of process is resumed, step-02 repeats.

Step-03:

After the frame number is obtained, it is combined with the page offset to generate the physical address.
Then, physical address is used to read the required word from the main memory.

Flowchart-

The following flowchart illustrates the above steps of translating logical address into physical address-

Page Fault Service Time-

The time taken by the page fault handling routine to service the page fault is called as page fault service time.
Page fault service time is much greater than main memory access time.
It increases the effective access time.

To gain better understanding about Page Fault in OS,

Watch this Video Lecture

Next Article- Page Replacement Algorithms

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Paging in OS | Practice Problems | Set-03

Operating System

Paging in OS-

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

We have discussed-

Paging is a non-contiguous memory allocation technique.
Page Table is a table that maps a page number to the frame number containing that page.
Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.
Translation Lookaside Buffer tries to reduce the effective access time.

Also Read- Important Formulas of Paging

In this article, we will discuss practice problems based on multilevel paging using TLB.

Effective Access Time-

In a multilevel paging scheme using TLB, the effective access time is given by-

This formula is valid only when there are no Page Faults.

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING AND TLB-

Problem-01:

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

Solution-

Given-

Number of levels of page table = 1
TLB access time = 20 ns
Main memory access time = 100 ns
TLB Hit ratio = 80% = 0.8

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

Calculating Effective Access Time-

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (1+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 220 ns

= 96 ns + 44 ns

= 140 ns

Thus, effective memory access time = 140 ns.

Problem-02:

Consider a two level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

Solution-

Given-

Number of levels of page table = 2
TLB access time = 20 ns
Main memory access time = 100 ns
TLB Hit ratio = 80% = 0.8

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

Calculating Effective Access Time-

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (2+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 320 ns

= 96 ns + 64 ns

= 160 ns

Thus, effective memory access time = 160 ns.

Problem-03:

Consider a three level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

Solution-

Given-

Number of levels of page table = 3
TLB access time = 20 ns
Main memory access time = 100 ns
TLB Hit ratio = 80% = 0.8

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

Calculating Effective Access Time-

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (3+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 420 ns

= 96 ns + 84 ns

= 180 ns

Thus, effective memory access time = 180 ns.

Problem-04:

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If effective memory access time is 130 ns, TLB hit ratio is ______.

Solution-

Given-

Number of levels of page table = 1
TLB access time = 20 ns
Main memory access time = 100 ns
Effective memory access time = 130 ns

Let TLB Hit ratio = H

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – H

Calculating TLB Hit Ratio-

Substituting values in the above formula, we get-

130 ns = H x { 20 ns + 100 ns } + (1-H) x { 20 ns + (1+1) x 100 ns }

130 ns = H x { 120 ns } + (1-H) x { 220 ns }

130 ns = 120H ns + 220 ns – 220H ns

220H ns – 120H ns = 220 ns – 130 ns

100H ns = 90 ns

H = 90 / 100

∴ H = 0.9

Thus, TLB hit ratio = 0.9 or 90%.

Problem-05:

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 100 ns to access the physical memory. If TLB hit ratio is 60% and effective memory access time is 160 ns, TLB access time is ______.

Solution-

Given-

Number of levels of page table = 1
Main memory access time = 100 ns
TLB Hit ratio = 60% = 0.6
Effective memory access time = 160 ns

Let TLB access time = T ns

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.6

= 0.4

Calculating TLB Access Time-

Substituting values in the above formula, we get-

160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + (1+1) x 100 ns }

160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + 200 ns }

160 ns = 0.6T ns + 60 ns + 0.4T ns + 80 ns

0.6T ns + 0.4T ns = 160 ns – 60 ns – 80 ns

T ns = 20 ns

∴ T = 20

Thus, TLB access time = 20 ns.

Problem-06:

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB. If TLB hit ratio is 50% and effective memory access time is 170 ns, main memory access time is ______.

Solution-

Given-

Number of levels of page table = 1
TLB access time = 20 ns
TLB Hit ratio = 50% = 0.5
Effective memory access time = 170 ns

Let main memory access time = T ns

Calculating TLB Miss Ratio-

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.5

= 0.5

Calculating Main Memory Access Time-

Substituting values in the above formula, we get-

170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + (1+1) x T ns }

170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + 2T ns }

170 ns = 10 ns + 0.5T ns + 10 ns + T ns

0.5T ns + T ns = 170 ns – 10 ns – 10 ns

1.5T ns = 150 ns

T = 150 / 1.5

∴ T = 100

Thus, Main Memory access time = 100 ns.

Next Article- Page Faults in OS

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Paging in OS | Practice Problems | Set-02

Operating System

Paging in OS-

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

We have discussed-

Paging is a non-contiguous memory allocation technique.
Page Table is a table that maps a page number to the frame number containing that page.
Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.

Also Read- Important Formulas of Paging

In this article, we will discuss practice problems based on multilevel paging.

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING IN OS-

Problem-01:

Consider a single level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of page table is 4 KB. Give the division of virtual address space.

Solution-

Given-

Page size = 4 KB
Page table entry size = 4 bytes
Page table size = 4 KB

Let the number of bits in virtual address = n bits

Number of Bits in Page Offset-

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

Process Size-

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

Number of Pages of Process-

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

Page Table Size-

Page table keeps track of the frames storing the pages of process.

Page table size

= Number of entries in page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

But we are given page table size = 4 KB

Thus,

2^n-10 bytes = 4 KB

2^n-10 = 2¹²

n – 10 = 12

∴ n = 22

Thus, number of bits in virtual address = 22 bits

Number of Bits Required to Search an Entry in Page Table-

Method-01:

Number of bits required to search a particular entry in page table

= Number of bits in virtual address – Number of bits in page offset

= 22 bits – 12 bits

= 10 bits

Method-02:

Number of entries in page table

= Number of pages the process is divided

= 2^n-12

= 2^22-12

= 2¹⁰

Thus, Number of bits required to search a particular entry in page table = 10 bits

Problem-02:

Consider a two level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outer page table is 4 KB. Give the division of virtual address space.

Solution-

Given-

Page size = 4 KB
Page table entry size = 4 bytes
Page table size = 4 KB

Let the number of bits in virtual address = n bits

Number of Bits in Page Offset-

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

Process Size-

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

Number of Pages of Process-

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

Inner Page Table Size-

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

Number of Pages of Inner Page Table-

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2^n-10 B / 4 KB

= 2^n-10 B / 2¹² B

= 2^n-10-12

= 2^n-22 pages

Now, these 2^n-22 pages of inner page table are stored in different frames of the main memory.

Number of Page Table Entries in One Page of Inner Page Table-

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

One page of inner page table contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

Outer Page Table Size-

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2^n-22 x 4 bytes

= 2^n-22+2 bytes

= 2^n-20 bytes

But we are given outer page table size = 4 KB

Thus,

2^n-20 bytes = 4 KB

2^n-20 = 2¹²

n – 20 = 12

∴ n = 32

Thus, number of bits in virtual address = 32 bits

Number of Bits Required to Search an Entry in Outer Page Table-

Method-01:

Number of bits required to search a particular entry in outer page table

= Number of bits in virtual address – (Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 32 bits – (10 bits + 12 bits)

= 32 bits – 22 bits

= 10 bits

Method-02:

Number of entries in outer page table

= Number of pages the inner page table is divided

= 2^n-22

= 2^32-22

= 2¹⁰

Thus, Number of bits required to search a particular entry in outer page table = 10 bits

Problem-03:

Consider a three level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outermost page table is 4 KB. Give the division of virtual address space.

Solution-

Given-

Page size = 4 KB
Page table entry size = 4 bytes
Page table size = 4 KB

Let the number of bits in virtual address = n bits

Number of Bits in Page Offset-

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

Process Size-

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

Number of Pages of Process-

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

Inner Page Table Size-

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

Number of Pages of Inner Page Table-

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2^n-10 B / 4 KB

= 2^n-10 B / 2¹² B

= 2^n-10-12

= 2^n-22 pages

Now, these 2^n-22 pages of inner page table are stored in different frames of the main memory.

Number of Page Table Entries in One Page of Inner Page Table-

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

One page of inner page table contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

Outer Page Table-1 Size-

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2^n-22 x 4 bytes

= 2^n-22+2 bytes

= 2^n-20 bytes

Number of Pages of Outer Page Table-1

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 2^n-20 B / 4 KB

= 2^n-20 B / 2¹² B

= 2^n-20-12

= 2^n-32 pages

Now, these 2^n-32 pages of outer page table-1 are stored in different frames of the main memory.

Number of Page Table Entries in One Page of Outer Page Table-1

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

One page of outer page table-1 contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 10 bits

Outer Page Table-2 Size-

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 2^n-32 x 4 bytes

= 2^n-32+2 bytes

= 2^n-30 bytes

But we are given outermost page table size = 4 KB

Thus,

2^n-30 bytes = 4 KB

2^n-30 = 2¹²

n – 30 = 12

∴ n = 42

Thus, number of bits in virtual address = 42 bits

Number of Bits Required to Search an Entry in Outer Page Table-2

Method-01:

Number of bits required to search a particular entry in outer page table-2

= Number of bits in virtual address – (Number of bits required to search an entry in outer page table-1 + Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 42 bits – (10 bits + 10 bits + 12 bits)

= 42 bits – 32 bits

= 10 bits

Method-02:

Number of entries in outer page table-2

= Number of pages the outer page table-1 is divided

= 2^n-32

= 2^42-32

= 2¹⁰

Thus, Number of bits required to search a particular entry in outer page table-2 = 10 bits

Problem-04:

Complete the following table-

Page Size	Page Table Entry Size	Outermost Page Table Size	Levels of Paging	Virtual Address Space Division
4 KB	4 bytes	256 bytes	1	?
4 KB	4 bytes	256 bytes	2	?
4 KB	4 bytes	256 bytes	3	?

Solution-

We have to solve these problems in exactly the same manner as we have solved above.
So, try yourself.

The answers to these problems are-

6 bits, 12 bits
6 bits, 10 bits, 12 bits
6 bits, 10 bits, 10 bits, 12 bits

Next Article- Practice Problems On Multilevel Paging Using TLB | Set-03

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

← Older Posts

Newer Posts →