Tag: Memory Management of OS

Paging in OS | Practice Problems | Set-01

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a table that maps a page number to the frame number containing that page.

 

Also Read- Important Formulas of Paging

 

In this article, we will discuss practice problems based on concepts of paging.

 

PRACTICE PROBLEMS BASED ON PAGING IN OS-

 

Problem-01:

 

Consider a single level paging scheme. The virtual address space is 4 MB and page size is 4 KB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 MB / 4 KB

= 210 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 210 x B bytes

 

Now,

According to the above condition, we must have-

210 x B bytes <= 4 KB

210 x B <= 212

B <= 4

Thus, maximum page table entry size possible = 4 bytes.

 

Problem-02:

 

Consider a single level paging scheme. The virtual address space is 4 GB and page size is 128 KB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 128 KB

= 232 B / 217 B

= 215 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 215 x B bytes

 

Now,

According to the above condition, we must have-

215 x B bytes <= 128 KB

215 x B <= 217

B <= 4

Thus, maximum page table entry size possible = 4 bytes.

 

Problem-03:

 

Consider a single level paging scheme. The virtual address space is 128 TB and page size is 32 MB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 128 TB / 32 MB

= 247 B / 225 B

= 222 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 222 x B bytes

 

Now,

According to the above condition, we must have-

222 x B bytes <= 32 MB

222 x B <= 225

B <= 8

Thus, maximum page table entry size possible = 8 bytes.

 

Problem-04:

 

Consider a single level paging scheme. The virtual address space is 256 MB and page table entry size is 4 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 256 MB / B bytes

= 228 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (228 / B) x 4 bytes

= (230 / B) bytes

 

Now,

According to the above condition, we must have-

(230 / B) bytes <= B bytes

B2 >= 230

B >= 215

Thus, minimum page size possible = 215 bytes or 32 KB.

 

Problem-05:

 

Consider a single level paging scheme. The virtual address space is 512 KB and page table entry size is 2 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 512 KB / B bytes

= 219 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (219 / B) x 2 bytes

= (220 / B) bytes

 

Now,

According to the above condition, we must have-

(220 / B) bytes <= B bytes

B2 >= 220

B >= 210

Thus, minimum page size possible = 210 bytes or 1 KB.

 

Problem-06:

 

Consider a single level paging scheme. The virtual address space is 16 GB and page table entry size is 4 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 16 GB / B bytes

= 234 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (234 / B) x 4 bytes

= (236 / B) bytes

 

Now,

According to the above condition, we must have-

(236 / B) bytes <= B bytes

B2 >= 236

B >= 218

Thus, minimum page size possible = 218 bytes or 256 KB.

 

Next Article- Translation Lookaside Buffer | TLB

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Multilevel Paging | Paging | Practice Problems

Operating System

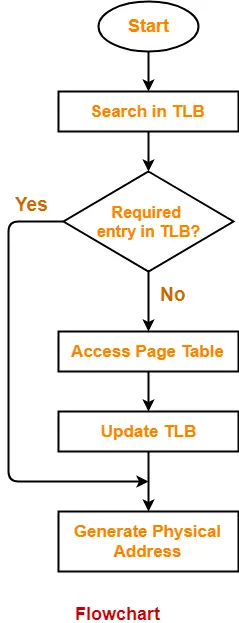
Multilevel Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Multilevel Paging.

 

We have discussed-

  • Multilevel Paging is a paging scheme where there exists a hierarchy of Page Tables.
  • Multilevel paging is needed when a page table can not be stored in a single frame due to its large size.

 

In this article, we will discuss practice problems based on multilevel paging.

 

Also Read- Paging Important Formulas

 

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING-

 

Problem-01:

 

Consider a system using multilevel paging scheme. The page size is 1 MB. The memory is byte addressable and virtual address is 64 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 64 bits
  • Page size = 1 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

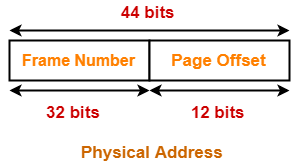
Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 1 MB

= 252 B

Thus, Number of bits in physical address = 52 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 1 MB

= 220 B

Thus, Number of bits in page offset = 20 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 52 bits – 32 bits

= 20 bits

 

Process Size-

 

Number of bits in virtual address = 64 bits

Thus,

Process size

= 264 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 264 B / 1 MB

= 264 B / 220 B

= 244 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 244 x 4 bytes

= 246 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (1 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 246 B / 1 MB

= 246 B / 220 B

= 226 pages

 

Now, these 226 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 1 MB / 4 B

= 220 B / 22 B

= 218 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 218 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 18 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 226 x 4 bytes

= 228 bytes

= 256 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (1 MB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 256 MB / 1 MB

= 256 pages

 

Now, these 256 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 1 MB / 4 B

= 220 B / 22 B

= 218 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 218 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 18 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 256 x 4 bytes

= 1 KB

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 KB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
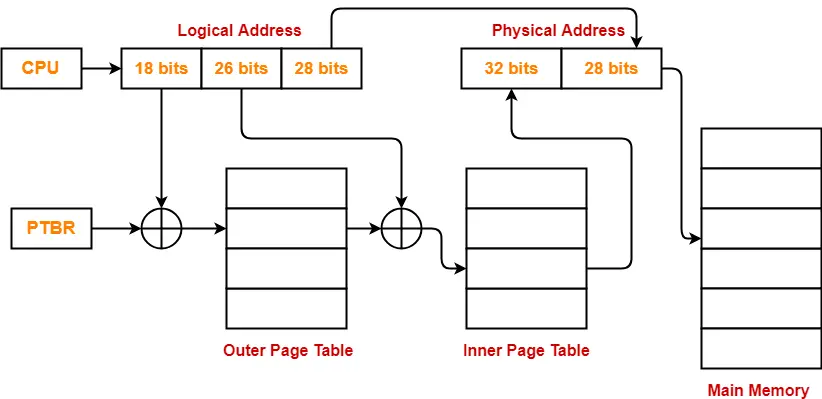
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 256 = 28 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 8 bits

 

The paging system will look like as shown below-

 

 

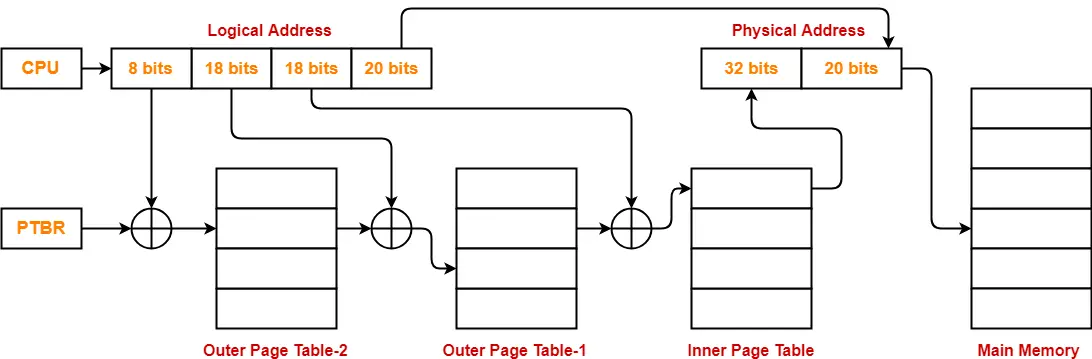
Problem-02:

 

Consider a system using multilevel paging scheme. The page size is 1 GB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 1 GB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 1 GB

= 262 B

Thus, Number of bits in physical address = 62 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 1 GB

= 230 B

Thus, Number of bits in page offset = 30 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 62 bits – 32 bits

= 30 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 1 GB

= 272 B / 230 B

= 242 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 242 x 4 bytes

= 244 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (1 GB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 244 B / 1 GB

= 244 B / 230 B

= 214 pages

 

Now, these 214 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 1 GB / 4 B

= 230 B / 22 B

= 228 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 228 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 28 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 214 x 4 bytes

= 216 bytes

= 64 KB

 

Now, we can observe-

  • The size of outer page table is less than the frame size (1 GB).
  • Thus, outer page table can be stored in a single frame.
  • In fact, outer page table will not completely occupy one frame and some space will remain vacant.
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 214 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 14 bits

 

The paging system will look like as shown below-

 

 

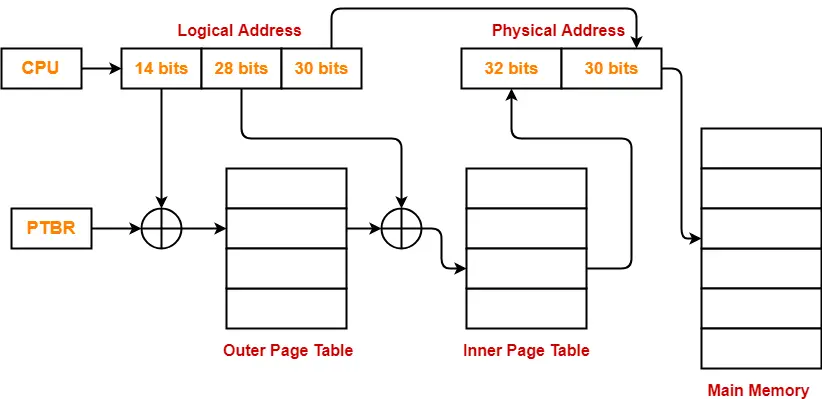
Problem-03:

 

Consider a system using multilevel paging scheme. The page size is 256 MB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 256 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 256 MB

= 260 B

Thus, Number of bits in physical address = 60 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 256 MB

= 228 B

Thus, Number of bits in page offset = 28 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 60 bits – 32 bits

= 28 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 256 MB

= 272 B / 228 B

= 244 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 244 x 4 bytes

= 246 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (256 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 246 B / 256 MB

= 246 B / 228 B

= 218 pages

 

Now, these 218 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 256 MB / 4 B

= 228 B / 22 B

= 226 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 226 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 26 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 218 x 4 bytes

= 220 bytes

= 1 MB

 

Now, we can observe-

  • The size of outer page table is less than the frame size (256 MB).
  • Thus, outer page table can be stored in a single frame.
  • In fact, outer page table will not completely occupy one frame and some space will remain vacant.
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 218 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 18 bits

 

The paging system will look like as shown below-

 

 

Problem-04:

 

Consider a system using multilevel paging scheme. The page size is 16 MB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 16 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 16 MB

= 256 B

Thus, Number of bits in physical address = 56 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 16 MB

= 224 B

Thus, Number of bits in page offset = 24 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 56 bits – 32 bits

= 24 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 16 MB

= 272 B / 224 B

= 248 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 248 x 4 bytes

= 250 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (16 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 250 B / 16 MB

= 250 B / 224 B

= 226 pages

 

Now, these 226 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 16 MB / 4 B

= 224 B / 22 B

= 222 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 222 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 22 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 226 x 4 bytes

= 228 bytes

= 256 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (16 MB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 256 MB / 16 MB

= 16 pages

 

Now, these 16 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 16 MB / 4 B

= 224 B / 22 B

= 222 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 222 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 22 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 16 x 4 bytes

= 64 bytes

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 MB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
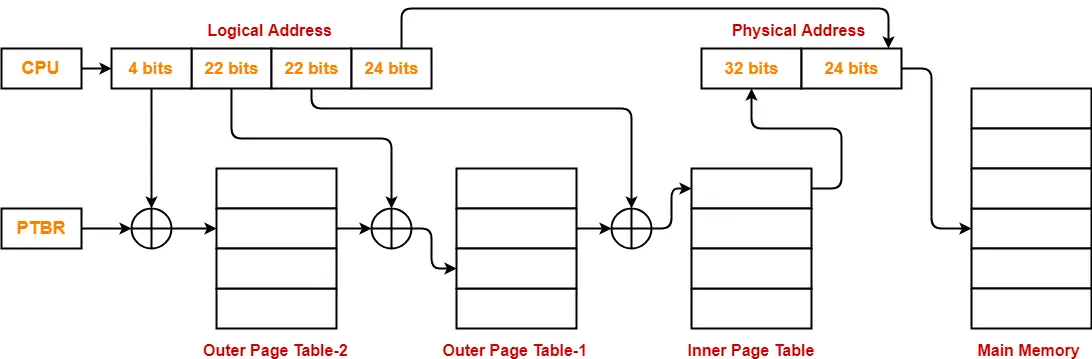
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 16 = 24 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 4 bits

 

The paging system will look like as shown below-

 

 

Next Article- Practice Problems On Multilevel Paging | Set-02

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Multilevel Paging in OS | Paging in OS

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a data structure that performs the mapping of page number to the frame number.

 

In this article, we will discuss about Multilevel Paging.

 

Multilevel Paging-

 

Multilevel paging is a paging scheme where there exists a hierarchy of page tables.

 

Need –

 

The need for multilevel paging arises when-

  • The size of page table is greater than the frame size.
  • As a result, the page table can not be stored in a single frame in main memory.

 

Working-

 

In multilevel paging,

  • The page table having size greater than the frame size is divided into several parts.
  • The size of each part is same as frame size except possibly the last part.
  • The pages of page table are then stored in different frames of the main memory.
  • To keep track of the frames storing the pages of the divided page table, another page table is maintained.
  • As a result, the hierarchy of page tables get generated.
  • Multilevel paging is done till the level is reached where the entire page table can be stored in a single frame.

 

Illustration of Multilevel Paging-

 

Consider a system using paging scheme where-

  • Logical Address Space = 4 GB
  • Physical Address Space = 16 TB
  • Page size = 4 KB

 

Now, let us find how many levels of page table will be required.

 

Number of Bits in Physical Address-

 

Size of main memory

= Physical Address Space

= 16 TB

= 244 B

Thus, Number of bits in physical address = 44 bits

 

Number of Frames in Main Memory-

 

Number of frames in main memory

= Size of main memory / Frame size

= 16 TB / 4 KB

= 232 frames

Thus, Number of bits in frame number = 32 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 44 bits – 32 bits

= 12 bits

 

So, Physical address is-

 

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 4 KB

= 220 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner Page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Number of bits in frame number

= 220 x 32 bits

= 220 x 4 bytes

= 4 MB

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (4 KB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 4 MB / 4 KB

= 210 pages

 

Now, these 210 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= Page size / Number of bits in frame number

= 4 KB / 32 bits

= 4 KB / 4 B

= 210

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer Page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Number of bits in frame number

= 210 x 32 bits

= 210 x 4 bytes

= 4 KB

 

Now, we can observe-

  • The size of outer page table is same as frame size (4 KB).
  • Thus, outer page table can be stored in a single frame.
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 10 bits

 

The paging system will look like as shown below-

 

 

PRACTICE PROBLEM BASED ON MULTILEVEL PAGING-

 

Problem-

 

Consider a system using multilevel paging scheme. The page size is 16 KB. The memory is byte addressable and virtual address is 48 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 48 bits
  • Page size = 16 KB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 16 KB

= 246 B

= 64 TB

Thus, Number of bits in physical address = 46 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 16 KB

= 214 B

Thus, Number of bits in page offset = 14 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 46 bits – 32 bits

= 14 bits

 

Process Size-

 

Number of bits in virtual address = 48 bits

Thus,

Process size

= 248 bytes

= 256 TB

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 256 TB / 16 KB

= 248 B / 214 B

= 234 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner Page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 234 x 4 bytes

= 236 bytes

= 64 GB

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (4 KB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 64 GB / 16 KB

= 236 B / 214 B

= 222 pages

 

Now, these 222 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 16 KB / 4 B

= 212 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 212 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 12 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer Page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 222 x 4 bytes

= 16 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (4 KB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 16 MB / 16 KB

= 210 pages

 

Now, these 210 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 16 KB / 4 B

= 212 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 212 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 12 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer Page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 210 x 4 bytes

= 4 KB

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 KB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 210 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 10 bits

 

The paging system will look like as shown below-

 

 

Important Points-

 

  • At any level, the page table entry size of any page table will always be same because each entry points to the frame number.
  • When there is only one level of paging, there is only one page table whose size is less than or equal to page size.
  • All the page tables are completely filled except possibly the last page.

 

To gain better understanding about Multilevel Paging,

Watch this Video Lecture

 

Next Article- Practice Problems On Multilevel Paging

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Translation Lookaside Buffer | TLB | Paging

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Paging in OS.

 

We have discussed-

  • Paging in OS is a non-contiguous memory allocation technique.
  • Page Table is a data structure that maps page number to the frame number.

 

Disadvantage Of Paging-

 

One major disadvantage of paging is-

  • It increases the effective access time due to increased number of memory accesses.
  • One memory access is required to get the frame number from the page table.
  • Another memory access is required to get the word from the page.

 

Translation Lookaside Buffer-

 

  • Translation Lookaside Buffer (TLB) is a solution that tries to reduce the effective access time.
  • Being a hardware, the access time of TLB is very less as compared to the main memory.

 

Structure-

 

Translation Lookaside Buffer (TLB) consists of two columns-

  1. Page Number
  2. Frame Number

 

 

Translating Logical Address into Physical Address-

 

In a paging scheme using TLB,

The logical address generated by the CPU is translated into the physical address using following steps-

 

Step-01:

 

CPU generates a logical address consisting of two parts-

  1. Page Number
  2. Page Offset

 

Step-02:

 

  • TLB is checked to see if it contains an entry for the referenced page number.
  • The referenced page number is compared with the TLB entries all at once.

 

Now, two cases are possible-

 

Case-01: If there is a TLB hit-

 

  • If TLB contains an entry for the referenced page number, a TLB hit occurs.
  • In this case, TLB entry is used to get the corresponding frame number for the referenced page number.

 

Case-02: If there is a TLB miss-

 

  • If TLB does not contain an entry for the referenced page number, a TLB miss occurs.
  • In this case, page table is used to get the corresponding frame number for the referenced page number.
  • Then, TLB is updated with the page number and frame number for future references.

 

Step-03:

 

  • After the frame number is obtained, it is combined with the page offset to generate the physical address.
  • Then, physical address is used to read the required word from the main memory.

 

NOTE-

 

In the above discussion, we have assumed that no Page Fault occurs.

 

Diagram-

 

The following diagram illustrates the above steps of translating logical address into physical address-

 

 

Flowchart-

 

The following flowchart illustrates the above steps of translating logical address into physical address-

 

 

Important Points-

 

Point-01:

 

  • Unlike page table, there exists only one TLB in the system.
  • So, whenever context switching occurs, the entire content of TLB is flushed and deleted.
  • TLB is then again updated with the currently running process.

 

Point-02:

 

When a new process gets scheduled-

  • Initially, TLB is empty. So, TLB misses are frequent.
  • With every access from the page table, TLB is updated.
  • After some time, TLB hits increases and TLB misses reduces.

 

Point-03:

 

  • The time taken to update TLB after getting the frame number from the page table is negligible.
  • Also, TLB is updated in parallel while fetching the word from the main memory.

 

Advantages-

 

The advantages of using TLB are-

  • TLB reduces the effective access time.
  • Only one memory access is required when TLB hit occurs.

 

Disadvantages-

 

A major disadvantage of using TLB is-

  • After some time of running the process, when TLB hits increases and process starts to run smoothly, a context switching occurs.
  • The entire content of the TLB is flushed.
  • Then, TLB is again updated with the currently running process.

This happens again and again.

 

Other disadvantages are-

  • TLB can hold the data of only one process at a time.
  • When context switches occur frequently, the performance of TLB degrades due to low hit ratio.
  • As it is a special hardware, it involves additional cost.

 

Effective Access Time-

 

In a single level paging using TLB, the effective access time is given as-

 

 

This formula is valid only when there is single level paging and there are no page faults.

 

PRACTICE PROBLEMS BASED ON TRANSLATION LOOKASIDE BUFFER-

 

Problem-01:

 

A paging scheme uses a Translation Lookaside buffer (TLB). A TLB access takes 10 ns and a main memory access takes 50 ns. What is the effective access time (in ns) if the TLB hit ratio is 90% and there is no page fault?

  1. 54
  2. 60
  3. 65
  4. 75

 

Solution-

 

Given-

  • TLB access time = 10 ns
  • Main memory access time = 50 ns
  • TLB Hit ratio = 90% = 0.9

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.9

= 0.1

 

Calculating Effective Access Time-

 

Substituting values in the above formula, we get-

Effective Access Time

= 0.9 x { 10 ns + 50 ns } + 0.1 x { 10 ns + 2 x 50 ns }

= 0.9 x 60 ns + 0.1 x 110 ns

= 54 ns + 11 ns

= 65 ns

Thus, Option (C) is correct.

 

Problem-02:

 

A paging scheme uses a Translation Lookaside buffer (TLB). The effective memory access takes 160 ns and a main memory access takes 100 ns. What is the TLB access time (in ns) if the TLB hit ratio is 60% and there is no page fault?

  1. 54
  2. 60
  3. 20
  4. 75

 

Solution-

 

Given-

  • Effective access time = 160 ns
  • Main memory access time = 100 ns
  • TLB Hit ratio = 60% = 0.6

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.6

= 0.4

 

Calculating TLB Access Time-

 

Let TLB access time = T ns.

Substituting values in the above formula, we get-

160 ns = 0.6 x { T + 100 ns } + 0.4 x { T + 2 x 100 ns }

160 = 0.6 x T + 60 + 0.4 x T + 80

160 = T + 140

T = 160 – 140

T = 20

 

Thus, Option (C) is correct.

 

To gain better understanding about Translation Lookaside Buffer (TLB),

Watch this Video Lecture

 

Next Article- Multilevel Paging

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Paging in OS | Formulas | Practice Problems

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a data structure that performs the mapping of page number to the frame number.

 

Important Formulas-

 

The following list of formulas is very useful for solving the numerical problems based on paging.

 

For Main Memory-

 

  • Physical Address Space = Size of main memory
  • Size of main memory = Total number of frames x Page size
  • Frame size = Page size
  • If number of frames in main memory = 2X, then number of bits in frame number = X bits
  • If Page size = 2X Bytes, then number of bits in page offset = X bits
  • If size of main memory = 2X Bytes, then number of bits in physical address = X bits

 

For Process-

 

  • Virtual Address Space = Size of process
  • Number of pages the process is divided = Process size / Page size
  • If process size = 2X bytes, then number of bits in virtual address space = X bits

 

For Page Table-

 

  • Size of page table = Number of entries in page table x Page table entry size
  • Number of entries in pages table = Number of pages the process is divided
  • Page table entry size = Number of bits in frame number + Number of bits used for optional fields if any

 

NOTE-

 

  • In general, if the given address consists of ‘n’ bits, then using ‘n’ bits, 2n locations are possible.
  • Then, size of memory = 2n x Size of one location.
  • If the memory is byte-addressable, then size of one location = 1 byte.
  • Thus, size of memory = 2n bytes.
  • If the memory is word-addressable where 1 word = m bytes, then size of one location = m bytes.
  • Thus, size of memory = 2n x m bytes.

 

PRACTICE PROBLEMS BASED ON PAGING AND PAGE TABLE-

 

Problem-01:

 

Calculate the size of memory if its address consists of 22 bits and the memory is 2-byte addressable.

 

Solution-

 

We have-

  • Number of locations possible with 22 bits = 222 locations
  • It is given that the size of one location = 2 bytes

 

Thus, Size of memory

= 222 x 2 bytes

= 223 bytes

= 8 MB

 

Problem-02:

 

Calculate the number of bits required in the address for memory having size of 16 GB. Assume the memory is 4-byte addressable.

 

Solution-

 

Let ‘n’ number of bits are required. Then, Size of memory = 2n x 4 bytes.

Since, the given memory has size of 16 GB, so we have-

2n x 4 bytes = 16 GB

2n x 4 = 16 G

2n x 22 = 234

2n = 232

∴ n = 32 bits

 

Problem-03:

 

Consider a system with byte-addressable memory, 32 bit logical addresses, 4 kilobyte page size and page table entries of 4 bytes each. The size of the page table in the system in megabytes is _____.

  1. 2
  2. 4
  3. 8
  4. 16

 

Solution-

 

Given-

  • Number of bits in logical address = 32 bits
  • Page size = 4KB
  • Page table entry size = 4 bytes

 

Process Size-

 

Number of bits in logical address = 32 bits

Thus,

Process size

= 232 B

= 4 GB

 

Number of Entries in Page Table-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 4 KB

= 220 pages

 

Thus,

Number of entries in page table = 220 entries

 

Page Table Size-

 

Page table size

= Number of entries in page table x Page table entry size

= 220 x 4 bytes

= 4 MB

 

Thus, Option (B) is correct.

 

Problem-04:

 

Consider a machine with 64 MB physical memory and a 32 bit virtual address space. If the page size is 4 KB, what is the approximate size of the page table?

  1. 16 MB
  2. 8 MB
  3. 2 MB
  4. 24 MB

 

Solution-

 

Given-

  • Size of main memory = 64 MB
  • Number of bits in virtual address space = 32 bits
  • Page size = 4 KB

 

We will consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

Size of main memory

= 64 MB

= 226 B

Thus, Number of bits in physical address = 26 bits

 

Number of Frames in Main Memory-

 

Number of frames in main memory

= Size of main memory / Frame size

= 64 MB / 4 KB

= 226 B / 212 B

= 214

Thus, Number of bits in frame number = 14 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

So, Physical address is-

 

 

Process Size-

 

Number of bits in virtual address space = 32 bits

Thus,

Process size

= 232 B

= 4 GB

 

Number of Entries in Page Table-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 4 KB

= 220 pages

 

Thus, Number of entries in page table = 220 entries

 

Page Table Size-

 

Page table size

= Number of entries in page table x Page table entry size

= Number of entries in page table x Number of bits in frame number

= 220 x 14 bits

= 220 x 16 bits      (Approximating 14 bits ≈ 16 bits)

= 220 x 2 bytes

= 2 MB

 

Thus, Option (C) is correct.

 

Problem-05:

 

In a virtual memory system, size of virtual address is 32-bit, size of physical address is 30-bit, page size is 4 Kbyte and size of each page table entry is 32-bit. The main memory is byte addressable. Which one of the following is the maximum number of bits that can be used for storing protection and other information in each page table entry?

  1. 2
  2. 10
  3. 12
  4. 14

 

Solution-

 

Given-

  • Number of bits in virtual address = 32 bits
  • Number of bits in physical address = 30 bits
  • Page size = 4 KB
  • Page table entry size = 32 bits

 

Size of Main Memory-

 

Number of bits in physical address = 30 bits

Thus,

Size of main memory

= 230 B

= 1 GB

 

Number of Frames in Main Memory-

 

Number of frames in main memory

= Size of main memory / Frame size

= 1 GB / 4 KB

= 230 B / 212 B

= 218

Thus, Number of bits in frame number = 18 bits

 

Number of Bits used for Storing other Information-

 

Maximum number of bits that can be used for storing protection and other information

= Page table entry size – Number of bits in frame number

= 32 bits – 18 bits

= 14 bits

 

Thus, Option (D) is correct.

 

To gain better understanding about solving numerical problems on paging,

Watch this Video Lecture

 

Next Article- Optimal Page Size | Practice Problems

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.