Huffman Coding-
- Huffman Coding is a famous Greedy Algorithm.
- It is used for the lossless compression of data.
- It uses variable length encoding.
- It assigns variable length code to all the characters.
- The code length of a character depends on how frequently it occurs in the given text.
- The character which occurs most frequently gets the smallest code.
- The character which occurs least frequently gets the largest code.
- It is also known as Huffman Encoding.
Prefix Rule-
- Huffman Coding implements a rule known as a prefix rule.
- This is to prevent the ambiguities while decoding.
- It ensures that the code assigned to any character is not a prefix of the code assigned to any other character.
Major Steps in Huffman Coding-
There are two major steps in Huffman Coding-
- Building a Huffman Tree from the input characters.
- Assigning code to the characters by traversing the Huffman Tree.
Huffman Tree-
The steps involved in the construction of Huffman Tree are as follows-
Step-01:
- Create a leaf node for each character of the text.
- Leaf node of a character contains the occurring frequency of that character.
Step-02:
- Arrange all the nodes in increasing order of their frequency value.
Step-03:
Considering the first two nodes having minimum frequency,
- Create a new internal node.
- The frequency of this new node is the sum of frequency of those two nodes.
- Make the first node as a left child and the other node as a right child of the newly created node.
Step-04:
- Keep repeating Step-02 and Step-03 until all the nodes form a single tree.
- The tree finally obtained is the desired Huffman Tree.
Time Complexity-
The time complexity analysis of Huffman Coding is as follows-
- extractMin( ) is called 2 x (n-1) times if there are n nodes.
- As extractMin( ) calls minHeapify( ), it takes O(logn) time.
Thus, Overall time complexity of Huffman Coding becomes O(nlogn).
Here, n is the number of unique characters in the given text.
Important Formulas-
The following 2 formulas are important to solve the problems based on Huffman Coding-
Formula-01:
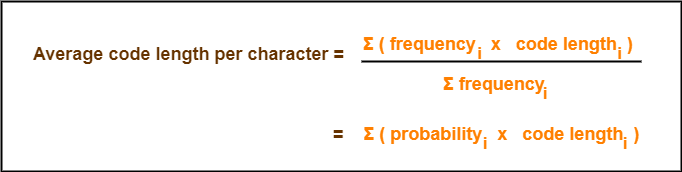
Formula-02:
Total number of bits in Huffman encoded message
= Total number of characters in the message x Average code length per character
= ∑ ( frequencyi x Code lengthi )
PRACTICE PROBLEM BASED ON HUFFMAN CODING-
Problem-
A file contains the following characters with the frequencies as shown. If Huffman Coding is used for data compression, determine-
- Huffman Code for each character
- Average code length
- Length of Huffman encoded message (in bits)
| Characters | Frequencies |
| a | 10 |
| e | 15 |
| i | 12 |
| o | 3 |
| u | 4 |
| s | 13 |
| t | 1 |
Solution-
First let us construct the Huffman Tree.
Huffman Tree is constructed in the following steps-
Step-01:

Step-02:
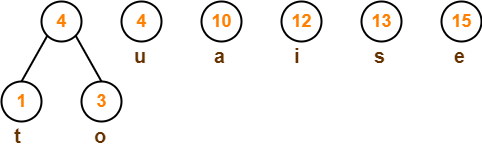
Step-03:
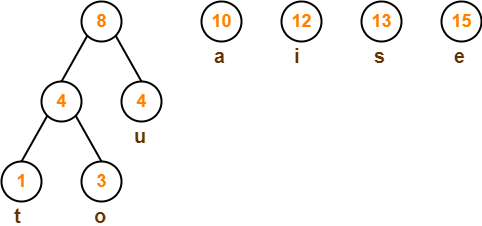
Step-04:
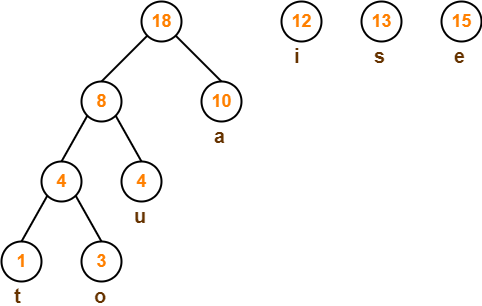
Step-05:
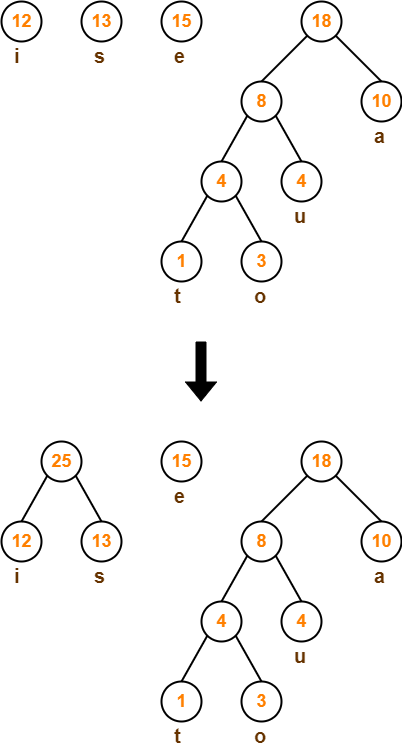
Step-06:
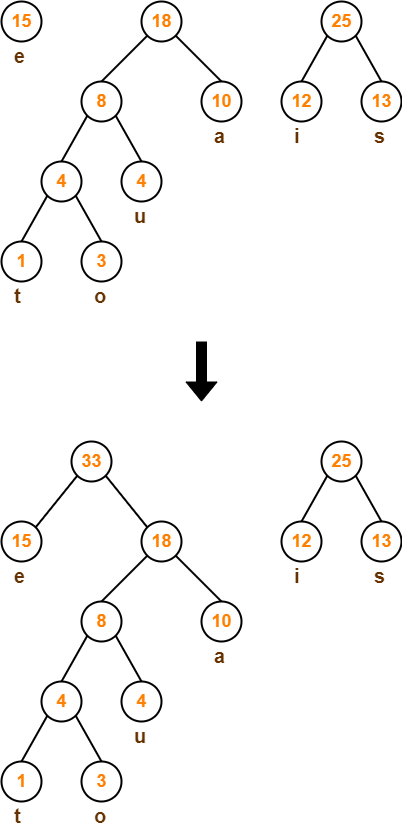
Step-07:
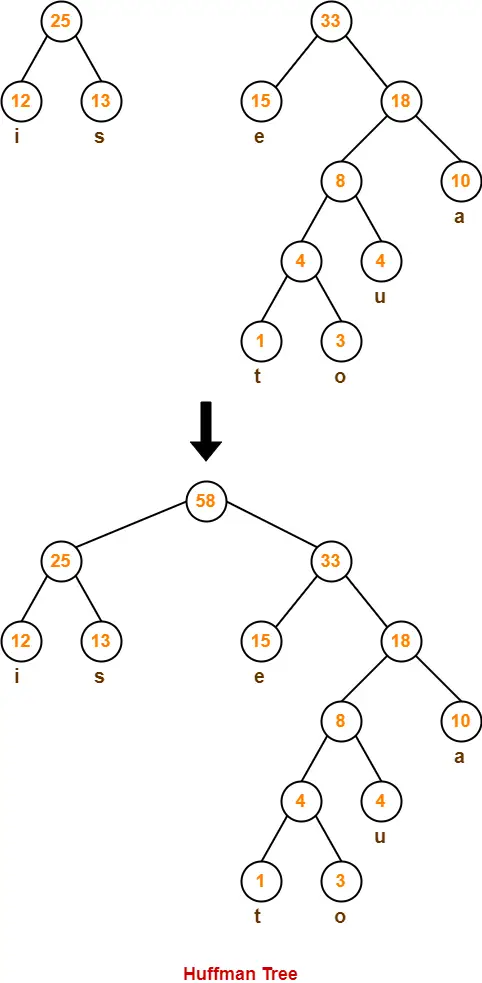
Now,
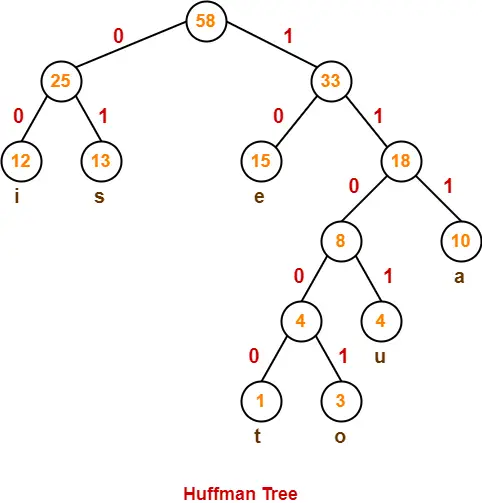
- We assign weight to all the edges of the constructed Huffman Tree.
- Let us assign weight ‘0’ to the left edges and weight ‘1’ to the right edges.
Rule
|
After assigning weight to all the edges, the modified Huffman Tree is-
Now, let us answer each part of the given problem one by one-
1. Huffman Code For Characters-
To write Huffman Code for any character, traverse the Huffman Tree from root node to the leaf node of that character.
Following this rule, the Huffman Code for each character is-
- a = 111
- e = 10
- i = 00
- o = 11001
- u = 1101
- s = 01
- t = 11000
From here, we can observe-
- Characters occurring less frequently in the text are assigned the larger code.
- Characters occurring more frequently in the text are assigned the smaller code.
2. Average Code Length-
Using formula-01, we have-
Average code length
= ∑ ( frequencyi x code lengthi ) / ∑ ( frequencyi )
= { (10 x 3) + (15 x 2) + (12 x 2) + (3 x 5) + (4 x 4) + (13 x 2) + (1 x 5) } / (10 + 15 + 12 + 3 + 4 + 13 + 1)
= 2.52
3. Length of Huffman Encoded Message-
Using formula-02, we have-
Total number of bits in Huffman encoded message
= Total number of characters in the message x Average code length per character
= 58 x 2.52
= 146.16
≅ 147 bits
To gain better understanding about Huffman Coding,
To practice previous years GATE problems on Huffman Coding,
Next Article- 0/1 Knapsack Problem
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.