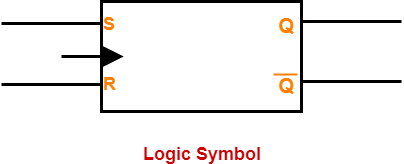Flip Flops-
Before you go through this article, make sure that you have gone through the previous article on Flip Flops.
We have discussed-
- A Flip Flop is a memory element that is capable of storing one bit of information.
- It is also called as Bistable Multivibrator since it has two stable states either 0 or 1.
There are following 4 basic types of flip flops-
- SR Flip Flop
- JK Flip Flop
- D Flip Flop
- T Flip Flop
In this article, we will discuss about JK Flip Flop.
JK Flip Flop-
| JK flip flop is a refined & improved version of SR Flip Flop
that has been introduced to solve the problem of indeterminate state
that occurs in SR flip flop when both the inputs are 1.
|
In JK flip flop,
- Input J behaves like input S of SR flip flop which was meant to set the flip flop.
- Input K behaves like input R of SR flip flop which was meant to reset the flip flop.
Construction of JK Flip Flop-
There are following two methods for constructing a JK flip flop-

- By using SR flip flop constructed from NOR latch
- By using SR flip flop constructed from NAND latch
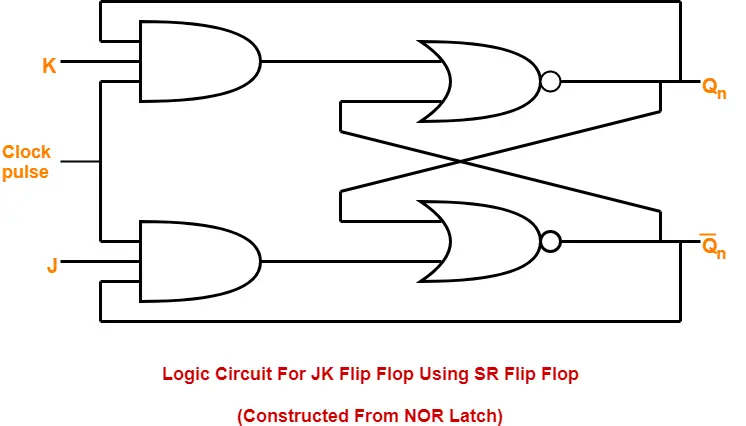
1. Construction of JK Flip Flop By Using SR Flip Flop Constructed From NOR Latch-
This method of constructing JK Flip Flop uses-
- SR Flip Flop constructed from NOR latch
- Two other connections
Logic Circuit-
The logic circuit for JK Flip Flop constructed using SR Flip Flop constructed from NOR latch is as shown below-
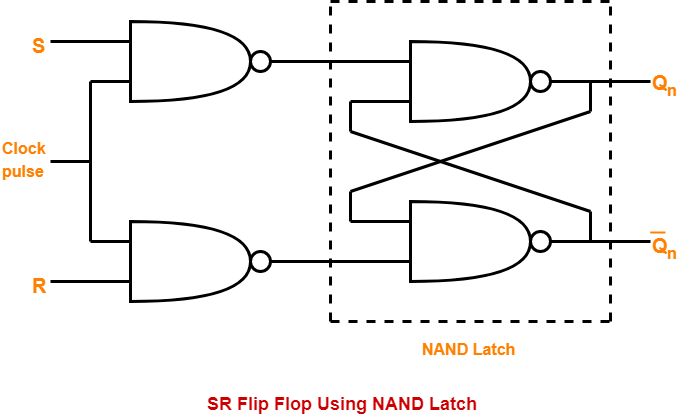
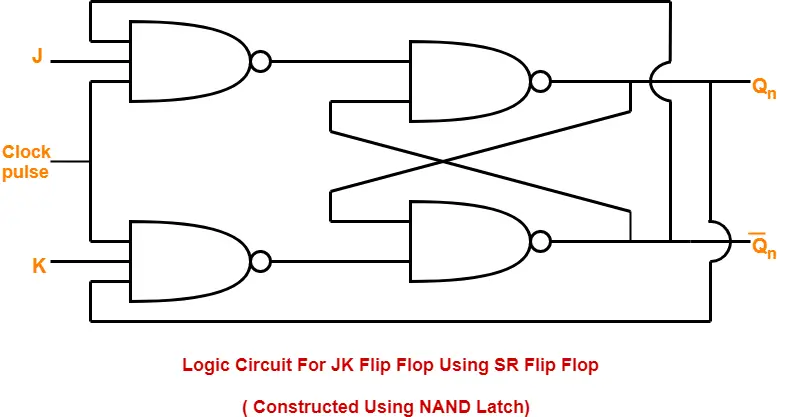
2. Construction of JK Flip Flop By Using SR Flip Flop Constructed From NAND Latch-
This method of constructing JK Flip Flop uses-
- SR Flip Flop constructed from NAND latch
- Two other connections
Logic Circuit-
The logic circuit for JK Flip Flop constructed using SR Flip Flop constructed from NAND latch is as shown below-
Logic Symbol-
The logic symbol for JK Flip Flop is as shown below-

Truth Table-
The truth table for JK Flip Flop is as shown below-
| INPUTS |
OUTPUTS |
| J |
K |
Qn
(Present State)
|
Qn+1
(Next State)
|
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
Truth Table
The above truth table may be reduced as-
| INPUTS |
OUTPUTS |
REMARKS |
| J |
K |
Qn
(Present State)
|
Qn+1
(Next State)
|
States and Conditions |
| 0 |
0 |
X |
Qn
|
Hold State condition J = K = 0 |
| 0 |
1 |
X |
0 |
Reset state condition J = 0 , K = 1 |
| 1 |
0 |
X |
1 |
Set state condition J = 1 , K = 0 |
| 1 |
1 |
X |
Q’n
|
Toggle state condition J = K = 1 |
Truth Table
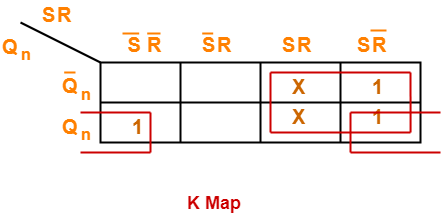
Characteristic Equation-
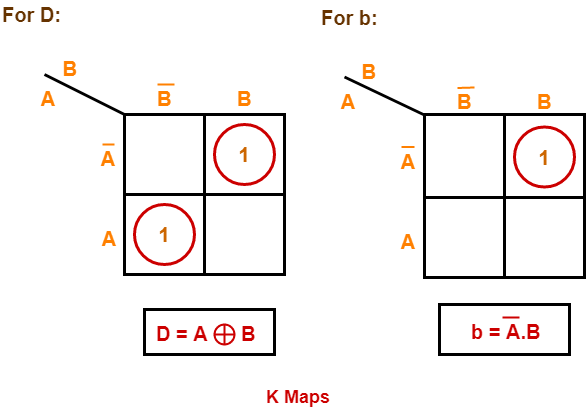
Draw a k map using the above truth table-
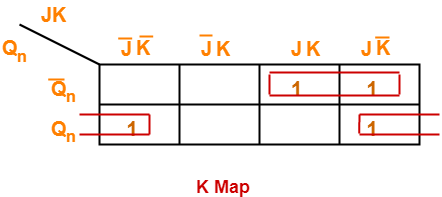
From here-
Qn+1 = Q’n (JK + JK’) + Qn (J’K’ + JK’)
Excitation Table-
The excitation table of any flip flop is drawn using its truth table.
|
What is excitation table?
For a given combination of present state Qn and next state Qn+1, excitation table tell the inputs required.
|
| Qn |
Qn+1 |
S |
R |
| 0 |
0 |
0 |
X |
| 0 |
1 |
1 |
X |
| 1 |
0 |
X |
1 |
| 1 |
1 |
X |
0 |
Excitation Table
SR Flip Flop Vs JK Flip Flop-
Both JK flip flop and SR flip flop are functionally same.
The only difference between them is-
- In JK flip flop, indeterminate state does not occur.
- In JK flip flop, instead of indeterminate state, the present state toggles.
- In other words, the present state gets inverted when both the inputs are 1.
To gain better understanding about JK Flip Flop,
Watch this Video Lecture
Next Article- Half Adder
Get more notes and other study material of Digital Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.