Tag: Demand Paging in OS

Paging in OS | Practice Problems | Set-03

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a table that maps a page number to the frame number containing that page.
  • Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.
  • Translation Lookaside Buffer tries to reduce the effective access time.

 

Also Read- Important Formulas of Paging

 

In this article, we will discuss practice problems based on multilevel paging using TLB.

 

Effective Access Time-

 

In a multilevel paging scheme using TLB, the effective access time is given by-

 

 

This formula is valid only when there are no Page Faults.

 

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING AND TLB-

 

Problem-01:

 

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

 

Solution-

 

Given-

  • Number of levels of page table = 1
  • TLB access time = 20 ns
  • Main memory access time = 100 ns
  • TLB Hit ratio = 80% = 0.8

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

 

Calculating Effective Access Time-

 

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (1+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 220 ns

= 96 ns + 44 ns

= 140 ns

Thus, effective memory access time = 140 ns.

 

Problem-02:

 

Consider a two level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

 

Solution-

 

Given-

  • Number of levels of page table = 2
  • TLB access time = 20 ns
  • Main memory access time = 100 ns
  • TLB Hit ratio = 80% = 0.8

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

 

Calculating Effective Access Time-

 

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (2+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 320 ns

= 96 ns + 64 ns

= 160 ns

Thus, effective memory access time = 160 ns.

 

Problem-03:

 

Consider a three level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.

 

Solution-

 

Given-

  • Number of levels of page table = 3
  • TLB access time = 20 ns
  • Main memory access time = 100 ns
  • TLB Hit ratio = 80% = 0.8

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.8

= 0.2

 

Calculating Effective Access Time-

 

Substituting values in the above formula, we get-

Effective Access Time

= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (3+1) x 100 ns }

= 0.8 x 120 ns + 0.2 + 420 ns

= 96 ns + 84 ns

= 180 ns

Thus, effective memory access time = 180 ns.

 

Problem-04:

 

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If effective memory access time is 130 ns, TLB hit ratio is ______.

 

Solution-

 

Given-

  • Number of levels of page table = 1
  • TLB access time = 20 ns
  • Main memory access time = 100 ns
  • Effective memory access time = 130 ns

 

Let TLB Hit ratio = H

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – H

 

Calculating TLB Hit Ratio-

 

Substituting values in the above formula, we get-

130 ns = H x { 20 ns + 100 ns } + (1-H) x { 20 ns + (1+1) x 100 ns }

130 ns = H x { 120 ns } + (1-H) x { 220 ns }

130 ns = 120H ns + 220 ns – 220H ns

220H ns – 120H ns = 220 ns – 130 ns

100H ns = 90 ns

H = 90 / 100

∴ H = 0.9

Thus, TLB hit ratio = 0.9 or 90%.

 

Problem-05:

 

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 100 ns to access the physical memory. If TLB hit ratio is 60% and effective memory access time is 160 ns, TLB access time is ______.

 

Solution-

 

Given-

  • Number of levels of page table = 1
  • Main memory access time = 100 ns
  • TLB Hit ratio = 60% = 0.6
  • Effective memory access time = 160 ns

 

Let TLB access time = T ns

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.6

= 0.4

 

Calculating TLB Access Time-

 

Substituting values in the above formula, we get-

160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + (1+1) x 100 ns }

160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + 200 ns }

160 ns = 0.6T ns + 60 ns + 0.4T ns + 80 ns

0.6T ns + 0.4T ns = 160 ns – 60 ns – 80 ns

T ns = 20 ns

∴ T = 20

Thus, TLB access time = 20 ns.

 

Problem-06:

 

Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB. If TLB hit ratio is 50% and effective memory access time is 170 ns, main memory access time is ______.

 

Solution-

 

Given-

  • Number of levels of page table = 1
  • TLB access time = 20 ns
  • TLB Hit ratio = 50% = 0.5
  • Effective memory access time = 170 ns

 

Let main memory access time = T ns

 

Calculating TLB Miss Ratio-

 

TLB Miss ratio

= 1 – TLB Hit ratio

= 1 – 0.5

= 0.5

 

Calculating Main Memory Access Time-

 

Substituting values in the above formula, we get-

170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + (1+1) x T ns }

170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + 2T ns }

170 ns = 10 ns + 0.5T ns + 10 ns + T ns

0.5T ns + T ns = 170 ns – 10 ns – 10 ns

1.5T ns = 150 ns

T = 150 / 1.5

∴ T = 100

Thus, Main Memory access time = 100 ns.

 

Next Article- Page Faults in OS

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Paging in OS | Practice Problems | Set-02

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a table that maps a page number to the frame number containing that page.
  • Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.

 

Also Read- Important Formulas of Paging

 

In this article, we will discuss practice problems based on multilevel paging.

 

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING IN OS-

 

Problem-01:

 

Consider a single level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

  • Page size = 4 KB
  • Page table entry size = 4 bytes
  • Page table size = 4 KB

 

Let the number of bits in virtual address = n bits

 

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2n bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2n B / 4 KB

= 2n B / 212 B

= 2n-12 pages

 

Page Table Size-

 

Page table keeps track of the frames storing the pages of process.

Page table size

= Number of entries in page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2n-12 x 4 bytes

= 2n-12+2 bytes

= 2n-10 bytes

 

But we are given page table size = 4 KB

Thus,

2n-10 bytes = 4 KB

2n-10 = 212

n – 10 = 12

∴ n = 22

Thus, number of bits in virtual address = 22 bits

 

 

Number of Bits Required to Search an Entry in Page Table-

 

Method-01:

 

Number of bits required to search a particular entry in page table

= Number of bits in virtual address – Number of bits in page offset

= 22 bits – 12 bits

= 10 bits

 

Method-02:

 

Number of entries in page table

= Number of pages the process is divided

= 2n-12

= 222-12

= 210

Thus, Number of bits required to search a particular entry in page table = 10 bits

 

 

Problem-02:

 

Consider a two level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outer page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

  • Page size = 4 KB
  • Page table entry size = 4 bytes
  • Page table size = 4 KB

 

Let the number of bits in virtual address = n bits

 

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2n bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2n B / 4 KB

= 2n B / 212 B

= 2n-12 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2n-12 x 4 bytes

= 2n-12+2 bytes

= 2n-10 bytes

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2n-10 B / 4 KB

= 2n-10 B / 212 B

= 2n-10-12

= 2n-22 pages

 

Now, these 2n-22 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 210 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2n-22 x 4 bytes

= 2n-22+2 bytes

= 2n-20 bytes

 

But we are given outer page table size = 4 KB

Thus,

2n-20 bytes = 4 KB

2n-20 = 212

n – 20 = 12

∴ n = 32

Thus, number of bits in virtual address = 32 bits

 

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Method-01:

 

Number of bits required to search a particular entry in outer page table

= Number of bits in virtual address – (Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 32 bits – (10 bits + 12 bits)

= 32 bits – 22 bits

= 10 bits

 

Method-02:

 

Number of entries in outer page table

= Number of pages the inner page table is divided

= 2n-22

= 232-22

= 210

Thus, Number of bits required to search a particular entry in outer page table = 10 bits

 

 

Problem-03:

 

Consider a three level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outermost page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

  • Page size = 4 KB
  • Page table entry size = 4 bytes
  • Page table size = 4 KB

 

Let the number of bits in virtual address = n bits

 

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2n bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2n B / 4 KB

= 2n B / 212 B

= 2n-12 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2n-12 x 4 bytes

= 2n-12+2 bytes

= 2n-10 bytes

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2n-10 B / 4 KB

= 2n-10 B / 212 B

= 2n-10-12

= 2n-22 pages

 

Now, these 2n-22 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 210 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2n-22 x 4 bytes

= 2n-22+2 bytes

= 2n-20 bytes

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 2n-20 B / 4 KB

= 2n-20 B / 212 B

= 2n-20-12

= 2n-32 pages

 

Now, these 2n-32 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 210 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 210 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 10 bits

 

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 2n-32 x 4 bytes

= 2n-32+2 bytes

= 2n-30 bytes

 

But we are given outermost page table size = 4 KB

Thus,

2n-30 bytes = 4 KB

2n-30 = 212

n – 30 = 12

∴ n = 42

Thus, number of bits in virtual address = 42 bits

 

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Method-01:

 

Number of bits required to search a particular entry in outer page table-2

= Number of bits in virtual address – (Number of bits required to search an entry in outer page table-1 + Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 42 bits – (10 bits + 10 bits + 12 bits)

= 42 bits – 32 bits

= 10 bits

 

Method-02:

 

Number of entries in outer page table-2

= Number of pages the outer page table-1 is divided

= 2n-32

= 242-32

= 210

Thus, Number of bits required to search a particular entry in outer page table-2 = 10 bits

 

 

Problem-04:

 

Complete the following table-

 

Page Size Page Table Entry Size Outermost Page Table Size Levels of Paging Virtual Address Space Division
4 KB 4 bytes 256 bytes 1 ?
4 KB 4 bytes 256 bytes 2 ?
4 KB 4 bytes 256 bytes 3 ?

 

Solution-

 

  • We have to solve these problems in exactly the same manner as we have solved above.
  • So, try yourself.

 

The answers to these problems are-

  1. 6 bits, 12 bits
  2. 6 bits, 10 bits, 12 bits
  3. 6 bits, 10 bits, 10 bits, 12 bits

 

Next Article- Practice Problems On Multilevel Paging Using TLB | Set-03

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Paging in OS | Practice Problems | Set-01

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a table that maps a page number to the frame number containing that page.

 

Also Read- Important Formulas of Paging

 

In this article, we will discuss practice problems based on concepts of paging.

 

PRACTICE PROBLEMS BASED ON PAGING IN OS-

 

Problem-01:

 

Consider a single level paging scheme. The virtual address space is 4 MB and page size is 4 KB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 MB / 4 KB

= 210 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 210 x B bytes

 

Now,

According to the above condition, we must have-

210 x B bytes <= 4 KB

210 x B <= 212

B <= 4

Thus, maximum page table entry size possible = 4 bytes.

 

Problem-02:

 

Consider a single level paging scheme. The virtual address space is 4 GB and page size is 128 KB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 128 KB

= 232 B / 217 B

= 215 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 215 x B bytes

 

Now,

According to the above condition, we must have-

215 x B bytes <= 128 KB

215 x B <= 217

B <= 4

Thus, maximum page table entry size possible = 4 bytes.

 

Problem-03:

 

Consider a single level paging scheme. The virtual address space is 128 TB and page size is 32 MB. What is the maximum page table entry size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 128 TB / 32 MB

= 247 B / 225 B

= 222 pages

 

Page Table Size-

 

Let page table entry size = B bytes

Now,

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 222 x B bytes

 

Now,

According to the above condition, we must have-

222 x B bytes <= 32 MB

222 x B <= 225

B <= 8

Thus, maximum page table entry size possible = 8 bytes.

 

Problem-04:

 

Consider a single level paging scheme. The virtual address space is 256 MB and page table entry size is 4 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 256 MB / B bytes

= 228 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (228 / B) x 4 bytes

= (230 / B) bytes

 

Now,

According to the above condition, we must have-

(230 / B) bytes <= B bytes

B2 >= 230

B >= 215

Thus, minimum page size possible = 215 bytes or 32 KB.

 

Problem-05:

 

Consider a single level paging scheme. The virtual address space is 512 KB and page table entry size is 2 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 512 KB / B bytes

= 219 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (219 / B) x 2 bytes

= (220 / B) bytes

 

Now,

According to the above condition, we must have-

(220 / B) bytes <= B bytes

B2 >= 220

B >= 210

Thus, minimum page size possible = 210 bytes or 1 KB.

 

Problem-06:

 

Consider a single level paging scheme. The virtual address space is 16 GB and page table entry size is 4 bytes. What is the minimum page size possible such that the entire page table fits well in one page?

 

Solution-

 

For page table, to fit well in one page, we must have-

Page table  size <= Page size

 

Let page size = B bytes.

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 16 GB / B bytes

= 234 / B

 

Page Table Size-

 

Page table size

= Number of entries in the page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= (234 / B) x 4 bytes

= (236 / B) bytes

 

Now,

According to the above condition, we must have-

(236 / B) bytes <= B bytes

B2 >= 236

B >= 218

Thus, minimum page size possible = 218 bytes or 256 KB.

 

Next Article- Translation Lookaside Buffer | TLB

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Multilevel Paging | Paging | Practice Problems

Operating System

Multilevel Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Multilevel Paging.

 

We have discussed-

  • Multilevel Paging is a paging scheme where there exists a hierarchy of Page Tables.
  • Multilevel paging is needed when a page table can not be stored in a single frame due to its large size.

 

In this article, we will discuss practice problems based on multilevel paging.

 

Also Read- Paging Important Formulas

 

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING-

 

Problem-01:

 

Consider a system using multilevel paging scheme. The page size is 1 MB. The memory is byte addressable and virtual address is 64 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 64 bits
  • Page size = 1 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

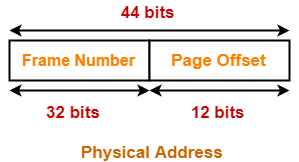
Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 1 MB

= 252 B

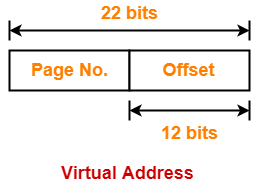
Thus, Number of bits in physical address = 52 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 1 MB

= 220 B

Thus, Number of bits in page offset = 20 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 52 bits – 32 bits

= 20 bits

 

Process Size-

 

Number of bits in virtual address = 64 bits

Thus,

Process size

= 264 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 264 B / 1 MB

= 264 B / 220 B

= 244 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 244 x 4 bytes

= 246 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (1 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 246 B / 1 MB

= 246 B / 220 B

= 226 pages

 

Now, these 226 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 1 MB / 4 B

= 220 B / 22 B

= 218 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 218 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 18 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 226 x 4 bytes

= 228 bytes

= 256 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (1 MB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 256 MB / 1 MB

= 256 pages

 

Now, these 256 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 1 MB / 4 B

= 220 B / 22 B

= 218 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 218 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 18 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 256 x 4 bytes

= 1 KB

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 KB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
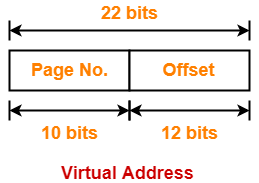
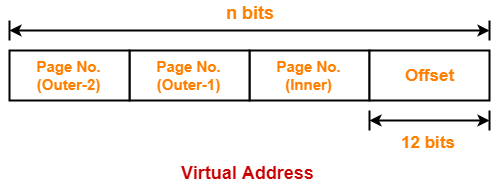
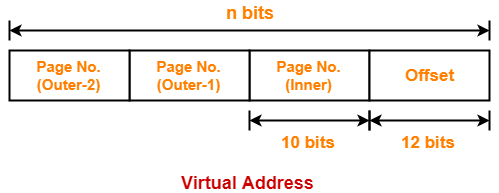
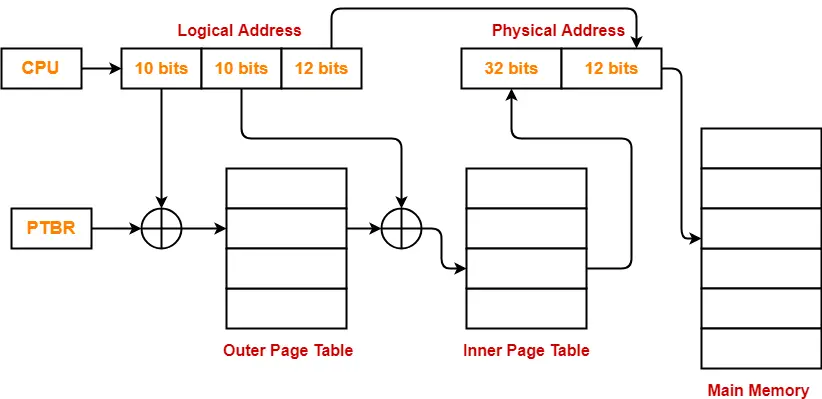
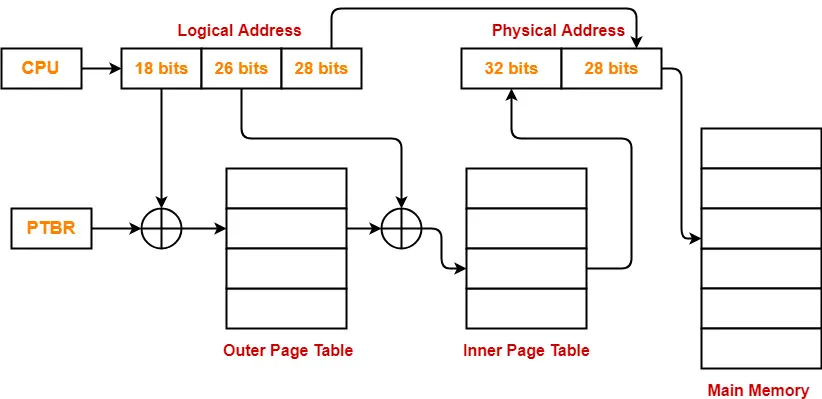
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 256 = 28 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 8 bits

 

The paging system will look like as shown below-

 

 

Problem-02:

 

Consider a system using multilevel paging scheme. The page size is 1 GB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 1 GB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 1 GB

= 262 B

Thus, Number of bits in physical address = 62 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 1 GB

= 230 B

Thus, Number of bits in page offset = 30 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 62 bits – 32 bits

= 30 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 1 GB

= 272 B / 230 B

= 242 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 242 x 4 bytes

= 244 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (1 GB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 244 B / 1 GB

= 244 B / 230 B

= 214 pages

 

Now, these 214 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 1 GB / 4 B

= 230 B / 22 B

= 228 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 228 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 28 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 214 x 4 bytes

= 216 bytes

= 64 KB

 

Now, we can observe-

  • The size of outer page table is less than the frame size (1 GB).
  • Thus, outer page table can be stored in a single frame.
  • In fact, outer page table will not completely occupy one frame and some space will remain vacant.
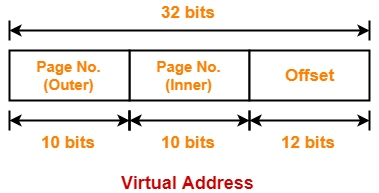
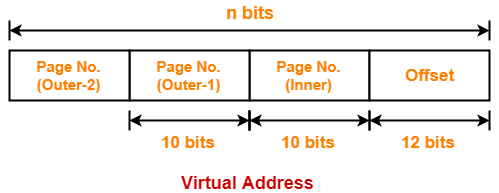
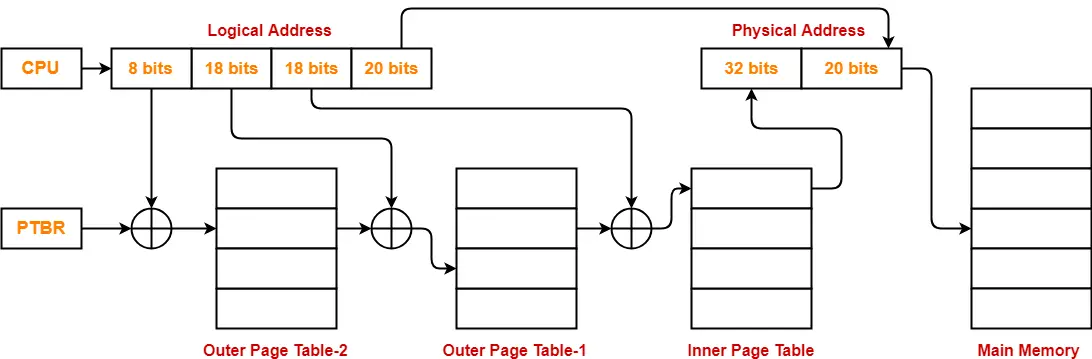
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 214 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 14 bits

 

The paging system will look like as shown below-

 

 

Problem-03:

 

Consider a system using multilevel paging scheme. The page size is 256 MB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 256 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 256 MB

= 260 B

Thus, Number of bits in physical address = 60 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 256 MB

= 228 B

Thus, Number of bits in page offset = 28 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 60 bits – 32 bits

= 28 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 256 MB

= 272 B / 228 B

= 244 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 244 x 4 bytes

= 246 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (256 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 246 B / 256 MB

= 246 B / 228 B

= 218 pages

 

Now, these 218 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 256 MB / 4 B

= 228 B / 22 B

= 226 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 226 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 26 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 218 x 4 bytes

= 220 bytes

= 1 MB

 

Now, we can observe-

  • The size of outer page table is less than the frame size (256 MB).
  • Thus, outer page table can be stored in a single frame.
  • In fact, outer page table will not completely occupy one frame and some space will remain vacant.
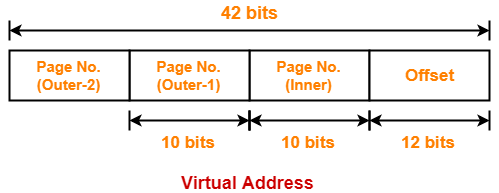
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 218 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 18 bits

 

The paging system will look like as shown below-

 

 

Problem-04:

 

Consider a system using multilevel paging scheme. The page size is 16 MB. The memory is byte addressable and virtual address is 72 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 72 bits
  • Page size = 16 MB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 16 MB

= 256 B

Thus, Number of bits in physical address = 56 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 16 MB

= 224 B

Thus, Number of bits in page offset = 24 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 56 bits – 32 bits

= 24 bits

 

Process Size-

 

Number of bits in virtual address = 72 bits

Thus,

Process size

= 272 bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 272 B / 16 MB

= 272 B / 224 B

= 248 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 248 x 4 bytes

= 250 bytes

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (16 MB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 250 B / 16 MB

= 250 B / 224 B

= 226 pages

 

Now, these 226 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 16 MB / 4 B

= 224 B / 22 B

= 222 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 222 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 22 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 226 x 4 bytes

= 228 bytes

= 256 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (16 MB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 256 MB / 16 MB

= 16 pages

 

Now, these 16 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 16 MB / 4 B

= 224 B / 22 B

= 222 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 222 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 22 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 16 x 4 bytes

= 64 bytes

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 MB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
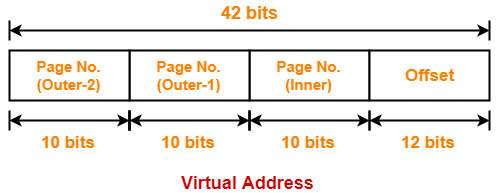
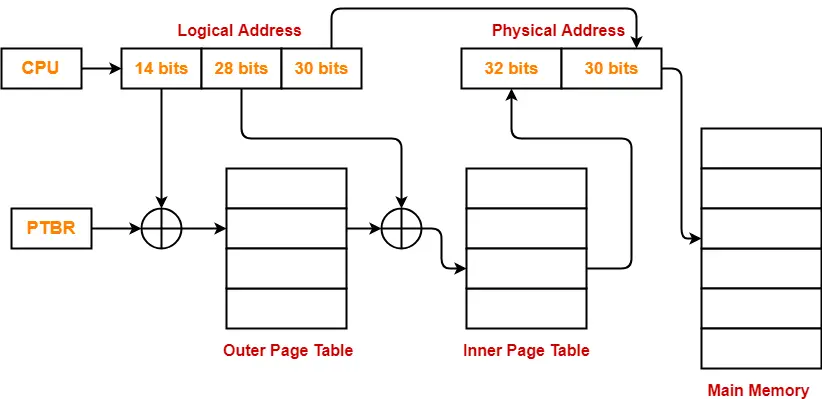
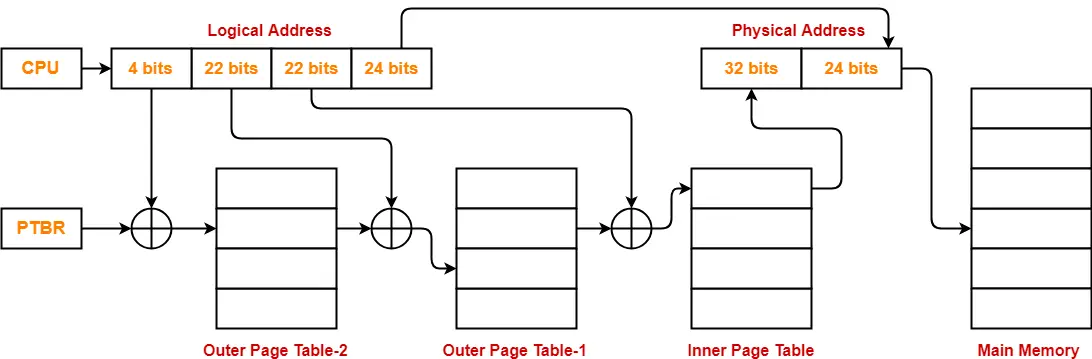
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 16 = 24 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 4 bits

 

The paging system will look like as shown below-

 

 

Next Article- Practice Problems On Multilevel Paging | Set-02

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Multilevel Paging in OS | Paging in OS

Operating System

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous article on Paging in OS.

 

We have discussed-

  • Paging is a non-contiguous memory allocation technique.
  • Page Table is a data structure that performs the mapping of page number to the frame number.

 

In this article, we will discuss about Multilevel Paging.

 

Multilevel Paging-

 

Multilevel paging is a paging scheme where there exists a hierarchy of page tables.

 

Need –

 

The need for multilevel paging arises when-

  • The size of page table is greater than the frame size.
  • As a result, the page table can not be stored in a single frame in main memory.

 

Working-

 

In multilevel paging,

  • The page table having size greater than the frame size is divided into several parts.
  • The size of each part is same as frame size except possibly the last part.
  • The pages of page table are then stored in different frames of the main memory.
  • To keep track of the frames storing the pages of the divided page table, another page table is maintained.
  • As a result, the hierarchy of page tables get generated.
  • Multilevel paging is done till the level is reached where the entire page table can be stored in a single frame.

 

Illustration of Multilevel Paging-

 

Consider a system using paging scheme where-

  • Logical Address Space = 4 GB
  • Physical Address Space = 16 TB
  • Page size = 4 KB

 

Now, let us find how many levels of page table will be required.

 

Number of Bits in Physical Address-

 

Size of main memory

= Physical Address Space

= 16 TB

= 244 B

Thus, Number of bits in physical address = 44 bits

 

Number of Frames in Main Memory-

 

Number of frames in main memory

= Size of main memory / Frame size

= 16 TB / 4 KB

= 232 frames

Thus, Number of bits in frame number = 32 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 212 B

Thus, Number of bits in page offset = 12 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 44 bits – 32 bits

= 12 bits

 

So, Physical address is-

 

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 4 GB / 4 KB

= 220 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner Page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Number of bits in frame number

= 220 x 32 bits

= 220 x 4 bytes

= 4 MB

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (4 KB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 4 MB / 4 KB

= 210 pages

 

Now, these 210 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= Page size / Number of bits in frame number

= 4 KB / 32 bits

= 4 KB / 4 B

= 210

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer Page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Number of bits in frame number

= 210 x 32 bits

= 210 x 4 bytes

= 4 KB

 

Now, we can observe-

  • The size of outer page table is same as frame size (4 KB).
  • Thus, outer page table can be stored in a single frame.
  • So, for given system, we will have two levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table.

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Outer page table contains 210 entries.

Thus,

Number of bits required to search a particular entry in outer page table = 10 bits

 

The paging system will look like as shown below-

 

 

PRACTICE PROBLEM BASED ON MULTILEVEL PAGING-

 

Problem-

 

Consider a system using multilevel paging scheme. The page size is 16 KB. The memory is byte addressable and virtual address is 48 bits long. The page table entry size is 4 bytes.

Find-

  1. How many levels of page table will be required?
  2. Give the divided physical address and virtual address.

 

Solution-

 

Given-

  • Virtual Address = 48 bits
  • Page size = 16 KB
  • Page table entry size = 4 bytes

 

Number of Bits in Frame Number-

 

We have,

Page table entry size

= 4 bytes

= 32 bits

Thus, Number of bits in frame number = 32 bits

 

Number of Frames in Main Memory-

 

We have, Number of bits in frame number = 32 bits

Thus,

Number of frames in main memory

= 232 frames

 

Size of Main Memory-

 

Size of main memory

= Total number of frames x Frame size

= 232 x 16 KB

= 246 B

= 64 TB

Thus, Number of bits in physical address = 46 bits

 

Number of Bits in Page Offset-

 

We have,

Page size

= 16 KB

= 214 B

Thus, Number of bits in page offset = 14 bits

 

Alternatively,

Number of bits in page offset

= Number of bits in physical address – Number of bits in frame number

= 46 bits – 32 bits

= 14 bits

 

Process Size-

 

Number of bits in virtual address = 48 bits

Thus,

Process size

= 248 bytes

= 256 TB

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 256 TB / 16 KB

= 248 B / 214 B

= 234 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner Page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 234 x 4 bytes

= 236 bytes

= 64 GB

 

Now, we can observe-

  • The size of inner page table is greater than the frame size (4 KB).
  • Thus, inner page table can not be stored in a single frame.
  • So, inner page table has to be divided into pages.

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 64 GB / 16 KB

= 236 B / 214 B

= 222 pages

 

Now, these 222 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 16 KB / 4 B

= 212 entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 212 entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 12 bits

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer Page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 222 x 4 bytes

= 16 MB

 

Now, we can observe-

  • The size of outer page table-1 is greater than the frame size (4 KB).
  • Thus, outer page table-1 can not be stored in a single frame.
  • So, outer page table-1 has to be divided into pages.

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 16 MB / 16 KB

= 210 pages

 

Now, these 210 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 16 KB / 4 B

= 212 entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 212 entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 12 bits

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer Page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 210 x 4 bytes

= 4 KB

 

Now, we can observe-

  • The size of outer page table-2 is less than the frame size (16 KB).
  • Thus, outer page table-2 can be stored in a single frame.
  • In fact, outer page table-2 will not completely occupy one frame and some space will remain vacant.
  • So, for given system, we will have three levels of page table.
  • Page Table Base Register (PTBR) will store the base address of the outer page table-2.

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Outer page table-2 contains 210 entries.

Thus,

Number of bits required to search a particular entry in outer page table-2 = 10 bits

 

The paging system will look like as shown below-

 

 

Important Points-

 

  • At any level, the page table entry size of any page table will always be same because each entry points to the frame number.
  • When there is only one level of paging, there is only one page table whose size is less than or equal to page size.
  • All the page tables are completely filled except possibly the last page.

 

To gain better understanding about Multilevel Paging,

Watch this Video Lecture

 

Next Article- Practice Problems On Multilevel Paging

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.