Binary Search Tree-
Before you go through this article, make sure that you have gone through the previous article on Binary Search Trees.
Binary search tree (BST) is a special kind of binary tree where each node contains-
- Only larger values in its right subtree.
- Only smaller values in its left subtree.
In this article, we will discuss about Binary Search Tree Operations.
Binary Search Tree Operations-
Commonly performed operations on binary search tree are-
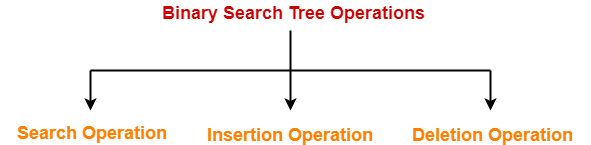
- Search Operation
- Insertion Operation
- Deletion Operation
1. Search Operation-
| Search Operation is performed to search a particular element in the Binary Search Tree. |
Rules-
For searching a given key in the BST,
- Compare the key with the value of root node.
- If the key is present at the root node, then return the root node.
- If the key is greater than the root node value, then recur for the root node’s right subtree.
- If the key is smaller than the root node value, then recur for the root node’s left subtree.
Example-
Consider key = 45 has to be searched in the given BST-
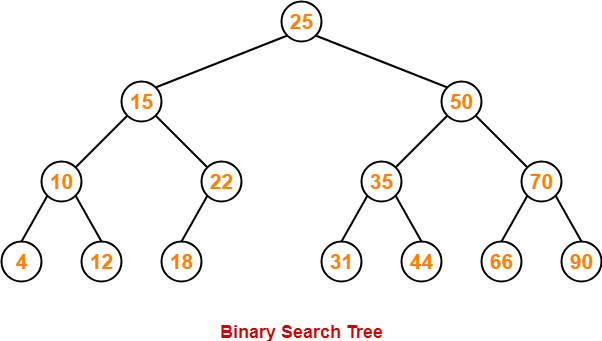
- We start our search from the root node 25.
- As 45 > 25, so we search in 25’s right subtree.
- As 45 < 50, so we search in 50’s left subtree.
- As 45 > 35, so we search in 35’s right subtree.
- As 45 > 44, so we search in 44’s right subtree but 44 has no subtrees.
- So, we conclude that 45 is not present in the above BST.
2. Insertion Operation-
| Insertion Operation is performed to insert an element in the Binary Search Tree. |
Rules-
The insertion of a new key always takes place as the child of some leaf node.
For finding out the suitable leaf node,
- Search the key to be inserted from the root node till some leaf node is reached.
- Once a leaf node is reached, insert the key as child of that leaf node.
Example-
Consider the following example where key = 40 is inserted in the given BST-
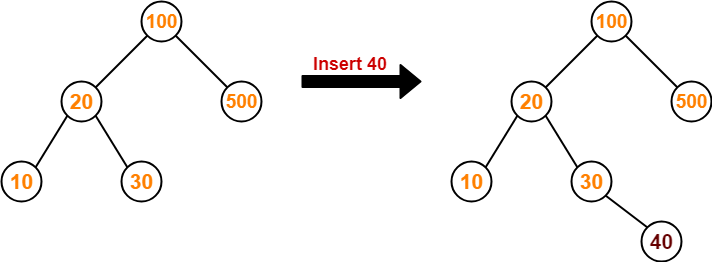
- We start searching for value 40 from the root node 100.
- As 40 < 100, so we search in 100’s left subtree.
- As 40 > 20, so we search in 20’s right subtree.
- As 40 > 30, so we add 40 to 30’s right subtree.
3. Deletion Operation-
| Deletion Operation is performed to delete a particular element from the Binary Search Tree. |
When it comes to deleting a node from the binary search tree, following three cases are possible-
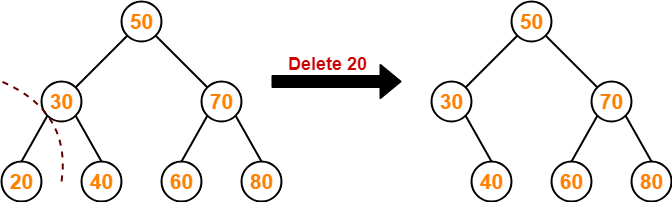
Case-01: Deletion Of A Node Having No Child (Leaf Node)-
Just remove / disconnect the leaf node that is to deleted from the tree.
Example-
Consider the following example where node with value = 20 is deleted from the BST-
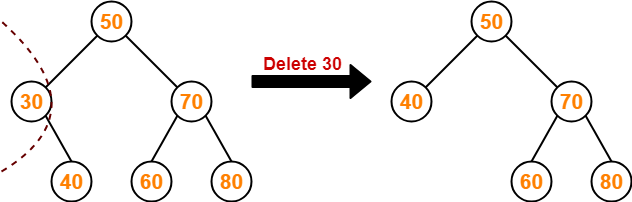
Case-02: Deletion Of A Node Having Only One Child-
Just make the child of the deleting node, the child of its grandparent.
Example-
Consider the following example where node with value = 30 is deleted from the BST-
Case-02: Deletion Of A Node Having Two Children-
A node with two children may be deleted from the BST in the following two ways-
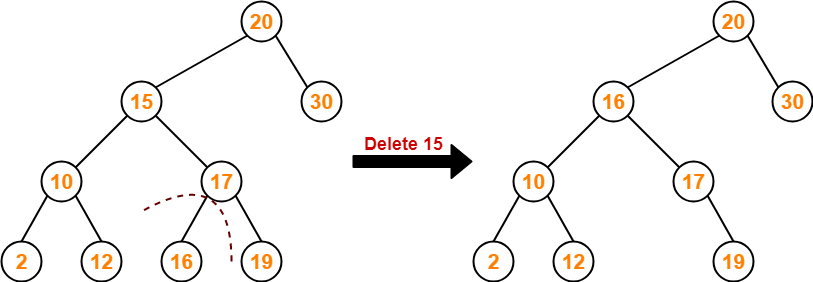
Method-01:
- Visit to the right subtree of the deleting node.
- Pluck the least value element called as inorder successor.
- Replace the deleting element with its inorder successor.
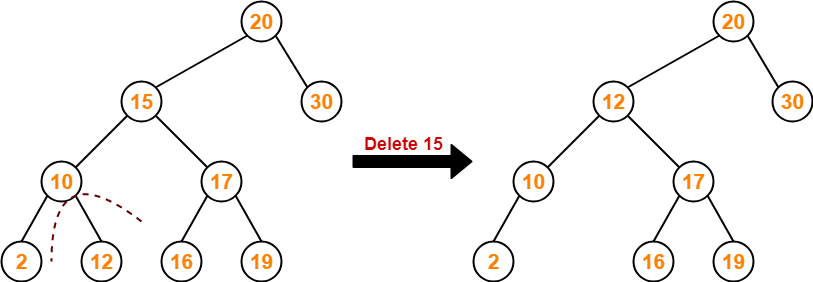
Example-
Consider the following example where node with value = 15 is deleted from the BST-
Method-02:
- Visit to the left subtree of the deleting node.
- Pluck the greatest value element called as inorder predecessor.
- Replace the deleting element with its inorder predecessor.
Example-
Consider the following example where node with value = 15 is deleted from the BST-
To gain better understanding about BST Operations,
Download Handwritten Notes Here-
Next Article- Time Complexity of BST Operations
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.