Tag: Data Structures and Algorithms

Floyd Warshall Algorithm | Example | Time Complexity

Design & Analysis of Algorithms

Floyd Warshall Algorithm-

 

  • Floyd Warshall Algorithm is a famous algorithm.
  • It is used to solve All Pairs Shortest Path Problem.
  • It computes the shortest path between every pair of vertices of the given graph.
  • Floyd Warshall Algorithm is an example of dynamic programming approach.

 

Also Read- Shortest Path Problem

 

Advantages-

 

Floyd Warshall Algorithm has the following main advantages-

  • It is extremely simple.
  • It is easy to implement.

 

Algorithm-

 

Floyd Warshall Algorithm is as shown below-

 

Create a |V| x |V| matrix               // It represents the distance between every pair of vertices as given

For each cell (i,j) in M do-

    if i = = j

        M[ i ][ j ] = 0                 // For all diagonal elements, value = 0

    if (i , j) is an edge in E

        M[ i ][ j ] = weight(i,j)       // If there exists a direct edge between the vertices, value = weight of edge

    else

        M[ i ][ j ] = infinity          // If there is no direct edge between the vertices, value = ∞

for k from 1 to |V|

    for i from 1 to |V|

        for j from 1 to |V|

            if M[ i ][ j ] > M[ i ][ k ] + M[ k ][ j ]
            M[ i ][ j ] = M[ i ][ k ] + M[ k ][ j ]

 

Time Complexity-

 

  • Floyd Warshall Algorithm consists of three loops over all the nodes.
  • The inner most loop consists of only constant complexity operations.
  • Hence, the asymptotic complexity of Floyd Warshall algorithm is O(n3).
  • Here, n is the number of nodes in the given graph.

 

When Floyd Warshall Algorithm Is Used?

 

  • Floyd Warshall Algorithm is best suited for dense graphs.
  • This is because its complexity depends only on the number of vertices in the given graph.
  • For sparse graphs, Johnson’s Algorithm is more suitable.

 

PRACTICE PROBLEM BASED ON FLOYD WARSHALL ALGORITHM-

 

Problem-

 

Consider the following directed weighted graph-

 

 

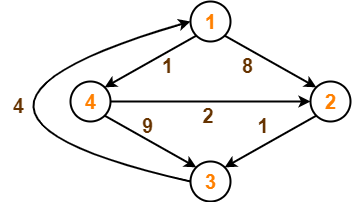
Using Floyd Warshall Algorithm, find the shortest path distance between every pair of vertices.

 

Solution-

 

Step-01:

 

  • Remove all the self loops and parallel edges (keeping the lowest weight edge) from the graph.
  • In the given graph, there are neither self edges nor parallel edges.

 

Step-02:

 

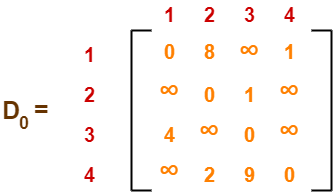
  • Write the initial distance matrix.
  • It represents the distance between every pair of vertices in the form of given weights.
  • For diagonal elements (representing self-loops), distance value = 0.
  • For vertices having a direct edge between them, distance value = weight of that edge.
  • For vertices having no direct edge between them, distance value = ∞.

 

Initial distance matrix for the given graph is-

 

 

Step-03:

 

Using Floyd Warshall Algorithm, write the following 4 matrices-

 

 

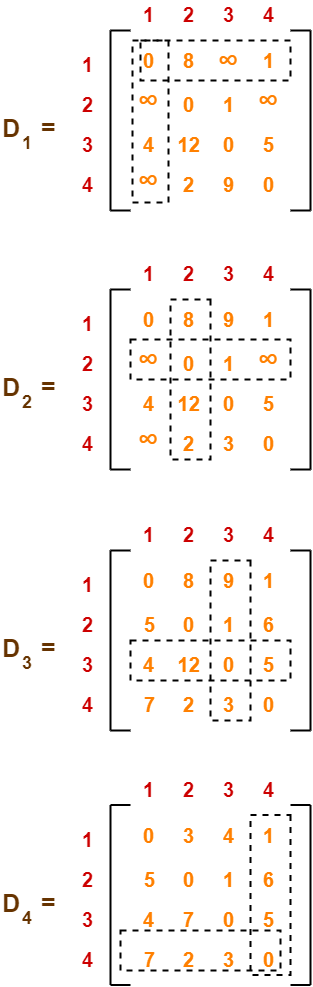
To learn how to write these matrices, watch this video here.

The last matrix D4 represents the shortest path distance between every pair of vertices.

 

Remember-

 

  • In the above problem, there are 4 vertices in the given graph.
  • So, there will be total 4 matrices of order 4 x 4 in the solution excluding the initial distance matrix.
  • Diagonal elements of each matrix will always be 0.

 

To gain better understanding about Floyd Warshall Algorithm,

Watch this Video Lecture

 

Next Article- Knapsack Problem

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Quick Sort Algorithm | Example | Time Complexity

Design & Analysis of Algorithms

Quick Sort-

 

  • Quick Sort is a famous sorting algorithm.
  • It sorts the given data items in ascending order.
  • It uses the idea of divide and conquer approach.
  • It follows a recursive algorithm.

 

Quick Sort Algorithm-

 

Consider-

  • a = Linear Array in memory
  • beg = Lower bound of the sub array in question
  • end = Upper bound of the sub array in question

 

Then, Quick Sort Algorithm is as follows-

 

Partition_Array (a , beg , end , loc)


Begin

Set left = beg , right = end , loc = beg

Set done = false

While (not done) do

    While ( (a[loc] <= a[right] ) and (loc ≠ right) ) do

    Set right = right - 1

    end while


    if (loc = right) then

    Set done = true

    else if (a[loc] > a[right]) then

        Interchange a[loc] and a[right]

        Set loc = right

    end if


    if (not done) then

    While ( (a[loc] >= a[left] ) and (loc ≠ left) ) do

    Set left = left + 1

    end while


    if (loc = left) then

    Set done = true

    else if (a[loc] < a[left]) then

        Interchange a[loc] and a[left]

        Set loc = left

    end if

    end if

end while

End

 

How Does Quick Sort Works?

 

  • Quick Sort follows a recursive algorithm.
  • It divides the given array into two sections using a partitioning element called as pivot.

 

The division performed is such that-

  • All the elements to the left side of pivot are smaller than pivot.
  • All the elements to the right side of pivot are greater than pivot.

 

After dividing the array into two sections, the pivot is set at its correct position.

Then, sub arrays are sorted separately by applying quick sort algorithm recursively.

 

Quick Sort Example-

 

Consider the following array has to be sorted in ascending order using quick sort algorithm-

 

 

Quick Sort Algorithm works in the following steps-

 

Step-01:

 

Initially-

  • Left and Loc (pivot) points to the first element of the array.
  • Right points to the last element of the array.

 

So to begin with, we set loc = 0, left = 0 and right = 5 as-

 

 

Step-02:

 

Since loc points at left, so algorithm starts from right and move towards left.

As a[loc] < a[right], so algorithm moves right one position towards left as-

 

 

Now, loc = 0, left = 0 and right = 4.

 

Step-03:

 

Since loc points at left, so algorithm starts from right and move towards left.

As a[loc] > a[right], so algorithm swaps a[loc] and a[right] and loc points at right as-

 

 

Now, loc = 4, left = 0 and right = 4.

 

Step-04:

 

Since loc points at right, so algorithm starts from left and move towards right.

As a[loc] > a[left], so algorithm moves left one position towards right as-

 

 

Now, loc = 4, left = 1 and right = 4.

 

Step-05:

 

Since loc points at right, so algorithm starts from left and move towards right.

As a[loc] > a[left], so algorithm moves left one position towards right as-

 

 

Now, loc = 4, left = 2 and right = 4.

 

Step-06:

 

Since loc points at right, so algorithm starts from left and move towards right.

As a[loc] < a[left], so we algorithm swaps a[loc] and a[left] and loc points at left as-

 

 

Now, loc = 2, left = 2 and right = 4.

 

Step-07:

 

Since loc points at left, so algorithm starts from right and move towards left.

As a[loc] < a[right], so algorithm moves right one position towards left as-

 

 

Now, loc = 2, left = 2 and right = 3.

 

Step-08:

 

Since loc points at left, so algorithm starts from right and move towards left.

As a[loc] > a[right], so algorithm swaps a[loc] and a[right] and loc points at right as-

 

 

Now, loc = 3, left = 2 and right = 3.

 

Step-09:

 

Since loc points at right, so algorithm starts from left and move towards right.

As a[loc] > a[left], so algorithm moves left one position towards right as-

 

 

Now, loc = 3, left = 3 and right = 3.

 

Now,

  • loc, left and right points at the same element.
  • This indicates the termination of procedure.
  • The pivot element 25 is placed in its final position.
  • All elements to the right side of element 25 are greater than it.
  • All elements to the left side of element 25 are smaller than it.

 

 

Now, quick sort algorithm is applied on the left and right sub arrays separately in the similar manner.

 

Quick Sort Analysis-

 

  • To find the location of an element that splits the array into two parts, O(n) operations are required.
  • This is because every element in the array is compared to the partitioning element.
  • After the division, each section is examined separately.
  • If the array is split approximately in half (which is not usually), then there will be log2n splits.
  • Therefore, total comparisons required are f(n) = n x log2n = O(nlog2n).

 

Order of Quick Sort = O(nlog2n)

 

Worst Case-

 

  • Quick Sort is sensitive to the order of input data.
  • It gives the worst performance when elements are already in the ascending order.
  • It then divides the array into sections of 1 and (n-1) elements in each call.
  • Then, there are (n-1) divisions in all.
  • Therefore, here total comparisons required are f(n) = n x (n-1) = O(n2).

 

Order of Quick Sort in worst case = O(n2)

 

Advantages of Quick Sort-

 

The advantages of quick sort algorithm are-

  • Quick Sort is an in-place sort, so it requires no temporary memory.
  • Quick Sort is typically faster than other algorithms.

(because its inner loop can be efficiently implemented on most architectures)

  • Quick Sort tends to make excellent usage of the memory hierarchy like virtual memory or caches.
  • Quick Sort can be easily parallelized due to its divide and conquer nature.

 

Disadvantages of Quick Sort-

 

The disadvantages of quick sort algorithm are-

  • The worst case complexity of quick sort is O(n2).
  • This complexity is worse than O(nlogn) worst case complexity of algorithms like merge sort, heap sort etc.
  • It is not a stable sort i.e. the order of equal elements may not be preserved.

 

To gain better understanding about Quick Sort Algorithm,

Watch this Video Lecture

 

Next Article- Topological Sort

 

Other Popular Sorting Algorithms-

 

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Algorithm | Example | Time Complexity

Design & Analysis of Algorithms

Searching-

 

  • Searching is a process of finding a particular element among several given elements.
  • The search is successful if the required element is found.
  • Otherwise, the search is unsuccessful.

 

Searching Algorithms-

 

Searching Algorithms are a family of algorithms used for the purpose of searching.

The searching of an element in the given array may be carried out in the following two ways-

 

 

  1. Linear Search
  2. Binary Search

 

In this article, we will discuss about Binary Search Algorithm.

 

Binary Search-

 

  • Binary Search is one of the fastest searching algorithms.
  • It is used for finding the location of an element in a linear array.
  • It works on the principle of divide and conquer technique.

 

Binary Search Algorithm can be applied only on Sorted arrays.

 

So, the elements must be arranged in-

  • Either ascending order if the elements are numbers.
  • Or dictionary order if the elements are strings.

 

To apply binary search on an unsorted array,

  • First, sort the array using some sorting technique.
  • Then, use binary search algorithm.

 

Also Read- Linear Search

 

Binary Search Algorithm-

 

Consider-

  • There is a linear array ‘a’ of size ‘n’.
  • Binary search algorithm is being used to search an element ‘item’ in this linear array.
  • If search ends in success, it sets loc to the index of the element otherwise it sets loc to -1.
  • Variables beg and end keeps track of the index of the first and last element of the array or sub array in which the element is being searched at that instant.
  • Variable mid keeps track of the index of the middle element of that array or sub array in which the element is being searched at that instant.

 

Then, Binary Search Algorithm is as follows-

 

Begin

Set beg = 0

Set end = n-1

Set mid = (beg + end) / 2

while ( (beg <= end) and (a[mid] ≠ item) ) do

    if (item < a[mid]) then

        Set end = mid - 1

    else

        Set beg = mid + 1

    endif

Set mid = (beg + end) / 2

endwhile

if (beg > end) then

    Set loc = -1

else

    Set loc = mid

endif

End

 

Explanation

 

Binary Search Algorithm searches an element by comparing it with the middle most element of the array.

Then, following three cases are possible-

 

Case-01

 

If the element being searched is found to be the middle most element, its index is returned.

 

Case-02

 

If the element being searched is found to be greater than the middle most element,

then its search is further continued in the right sub array of the middle most element.

 

Case-03

 

If the element being searched is found to be smaller than the middle most element,

then its search is further continued in the left sub array of the middle most element.

 

This iteration keeps on repeating on the sub arrays until the desired element is found

or size of the sub array reduces to zero.

 

Time Complexity Analysis-

 

Binary Search time complexity analysis is done below-

  • In each iteration or in each recursive call, the search gets reduced to half of the array.
  • So for n elements in the array, there are log2n iterations or recursive calls.

 

Thus, we have-

 

Time Complexity of Binary Search Algorithm is O(log2n).

Here, n is the number of elements in the sorted linear array.

 

This time complexity of binary search remains unchanged irrespective of the element position even if it is not present in the array.

 

Binary Search Example-

 

Consider-

  • We are given the following sorted linear array.
  • Element 15 has to be searched in it using Binary Search Algorithm.

 

 

Binary Search Algorithm works in the following steps-

 

Step-01:

 

  • To begin with, we take beg=0 and end=6.
  • We compute location of the middle element as-

mid

= (beg + end) / 2

= (0 + 6) / 2

= 3

  • Here, a[mid] = a[3] = 20 ≠ 15 and beg < end.
  • So, we start next iteration.

 

Step-02:

 

  • Since a[mid] = 20 > 15, so we take end = mid – 1 = 3 – 1 = 2 whereas beg remains unchanged.
  • We compute location of the middle element as-

mid

= (beg + end) / 2

= (0 + 2) / 2

= 1

  • Here, a[mid] = a[1] = 10 ≠ 15 and beg < end.
  • So, we start next iteration.

 

Step-03:

 

  • Since a[mid] = 10 < 15, so we take beg = mid + 1 = 1 + 1 = 2 whereas end remains unchanged.
  • We compute location of the middle element as-

mid

= (beg + end) / 2

= (2 + 2) / 2

= 2

  • Here, a[mid] = a[2] = 15 which matches to the element being searched.
  • So, our search terminates in success and index 2 is returned.

 

Binary Search Algorithm Advantages-

 

The advantages of binary search algorithm are-

  • It eliminates half of the list from further searching by using the result of each comparison.
  • It indicates whether the element being searched is before or after the current position in the list.
  • This information is used to narrow the search.
  • For large lists of data, it works significantly better than linear search.

 

Binary Search Algorithm Disadvantages-

 

The disadvantages of binary search algorithm are-

  • It employs recursive approach which requires more stack space.
  • Programming binary search algorithm is error prone and difficult.
  • The interaction of binary search with memory hierarchy i.e. caching is poor.

(because of its random access nature)

 

Important Note-

 

For in-memory searching, if the interval to be searched is small,

  • Linear search may exhibit better performance than binary search.
  • This is because it exhibits better locality of reference.

 

To gain better understanding about Binary Search Algorithm,

Watch this Video Lecture

 

Next Article- Selection Sort

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Linear Search Algorithm | Example | Time Complexity

Design & Analysis of Algorithms

Searching-

 

  • Searching is a process of finding a particular element among several given elements.
  • The search is successful if the required element is found.
  • Otherwise, the search is unsuccessful.

 

Searching Algorithms-

 

Searching Algorithms are a family of algorithms used for the purpose of searching.

The searching of an element in the given array may be carried out in the following two ways-

 

 

  1. Linear Search
  2. Binary Search

 

In this article, we will discuss about Linear Search Algorithm.

 

Linear Search-

 

  • Linear Search is the simplest searching algorithm.
  • It traverses the array sequentially to locate the required element.
  • It searches for an element by comparing it with each element of the array one by one.
  • So, it is also called as Sequential Search.

 

Linear Search Algorithm is applied when-

  • No information is given about the array.
  • The given array is unsorted or the elements are unordered.
  • The list of data items is smaller.

 

Linear Search Algorithm-

 

Consider-

  • There is a linear array ‘a’ of size ‘n’.
  • Linear search algorithm is being used to search an element ‘item’ in this linear array.
  • If search ends in success, it sets loc to the index of the element otherwise it sets loc to -1.

 

Then, Linear Search Algorithm is as follows-

 

Linear_Search (a , n , item , loc)

 

Begin

for i = 0 to (n - 1) by 1 do

    if (a[i] = item) then

        set loc = i

        Exit

    endif

endfor

set loc = -1

End

 

Time Complexity Analysis-

 

Linear Search time complexity analysis is done below-

 

Best case-

 

In the best possible case,

  • The element being searched may be found at the first position.
  • In this case, the search terminates in success with just one comparison.
  • Thus in best case, linear search algorithm takes O(1) operations.

 

Worst Case-

 

In the worst possible case,

  • The element being searched may be present at the last position or not present in the array at all.
  • In the former case, the search terminates in success with n comparisons.
  • In the later case, the search terminates in failure with n comparisons.
  • Thus in worst case, linear search algorithm takes O(n) operations.

 

Thus, we have-

 

Time Complexity of Linear Search Algorithm is O(n).

Here, n is the number of elements in the linear array.

 

Linear Search Efficiency-

 

  • Linear Search is less efficient when compared with other algorithms like Binary Search & Hash tables.
  • The other algorithms allow significantly faster searching.

 

Linear Search Example-

 

Consider-

  • We are given the following linear array.
  • Element 15 has to be searched in it using Linear Search Algorithm.

 

 

Now,

  • Linear Search algorithm compares element 15 with all the elements of the array one by one.
  • It continues searching until either the element 15 is found or all the elements are searched.

 

Linear Search Algorithm works in the following steps-

 

Step-01:

 

  • It compares element 15 with the 1st element 92.
  • Since 15 ≠ 92, so required element is not found.
  • So, it moves to the next element.

 

Step-02:

 

  • It compares element 15 with the 2nd element 87.
  • Since 15 ≠ 87, so required element is not found.
  • So, it moves to the next element.

 

Step-03:

 

  • It compares element 15 with the 3rd element 53.
  • Since 15 ≠ 53, so required element is not found.
  • So, it moves to the next element.

 

Step-04:

 

  • It compares element 15 with the 4th element 10.
  • Since 15 ≠ 10, so required element is not found.
  • So, it moves to the next element.

 

Step-05:

 

  • It compares element 15 with the 5th element 15.
  • Since 15 = 15, so required element is found.
  • Now, it stops the comparison and returns index 4 at which element 15 is present.

 

To gain better understanding about Linear Search Algorithm,

Watch this Video Lecture

 

Next Article- Binary Search

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Shortest Path Problem | Shortest Path Algorithms | Examples

Design & Analysis of Algorithms

Shortest Path Problem-

 

In data structures,

  • Shortest path problem is a problem of finding the shortest path(s) between vertices of a given graph.
  • Shortest path between two vertices is a path that has the least cost as compared to all other existing paths.

 

Shortest Path Algorithms-

 

Shortest path algorithms are a family of algorithms used for solving the shortest path problem.

 

Applications-

 

Shortest path algorithms have a wide range of applications such as in-

  • Google Maps
  • Road Networks
  • Logistics Research

 

Types of Shortest Path Problem-

 

Various types of shortest path problem are-

 

 

  1. Single-pair shortest path problem
  2. Single-source shortest path problem
  3. Single-destination shortest path problem
  4. All pairs shortest path problem

 

Single-Pair Shortest Path Problem-

 

  • It is a shortest path problem where the shortest path between a given pair of vertices is computed.
  • A* Search Algorithm is a famous algorithm used for solving single-pair shortest path problem.

 

Single-Source Shortest Path Problem-

 

  • It is a shortest path problem where the shortest path from a given source vertex to all other remaining vertices is computed.
  • Dijkstra’s Algorithm and Bellman Ford Algorithm are the famous algorithms used for solving single-source shortest path problem.

 

Single-Destination Shortest Path Problem-

 

  • It is a shortest path problem where the shortest path from all the vertices to a single destination vertex is computed.
  • By reversing the direction of each edge in the graph, this problem reduces to single-source shortest path problem.
  • Dijkstra’s Algorithm is a famous algorithm adapted for solving single-destination shortest path problem.

 

All Pairs Shortest Path Problem-

 

  • It is a shortest path problem where the shortest path between every pair of vertices is computed.
  • Floyd-Warshall Algorithm and Johnson’s Algorithm are the famous algorithms used for solving All pairs shortest path problem.

 

Also Read- Floyd-Warshall Algorithm

 

Next Article- Dijkstra’s Algorithm

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.