Computer Organization and Architecture PDF

Tag: Computer Organization and Architecture PDF

Cache Line | Cache Line Size | Cache Memory

Computer Organization and Architecture

Cache Memory-

Before you go through this article, make sure that you have gone through the previous article on Cache Memory.

We have discussed-

Cache memory is a random access memory.
It lies on the path between the processor and the main memory.
It bridges the speed mismatch between the fastest processor and the slower main memory.

Also Read- Cache Mapping Techniques

Cache Lines-

Cache memory is divided into equal size partitions called as cache lines.

While designing a computer’s cache system, the size of cache lines is an important parameter.
The size of cache line affects a lot of parameters in the caching system.

The following results discuss the effect of changing the cache block (or line) size in a caching system.

Result-01: Effect of Changing Block Size on Spatial Locality-

The larger the block size, better will be the spatial locality.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

A smaller block size will contain a smaller number of near by addresses in it.
Thus, only smaller number of near by addresses will be brought into the cache.
This increases the chances of cache miss which reduces the exploitation of spatial locality.
Thus, smaller is the block size, inferior is the spatial locality.

Case-02: Increasing the Block Size-

A larger block size will contain a larger number of near by addresses in it.
Thus, larger number of near by addresses will be brought into the cache.
This increases the chances of cache hit which increases the exploitation of spatial locality.
Thus, larger is the block size, better is the spatial locality.

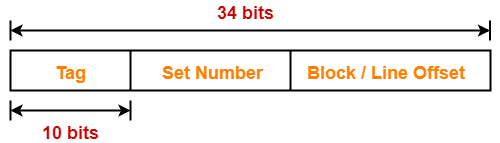
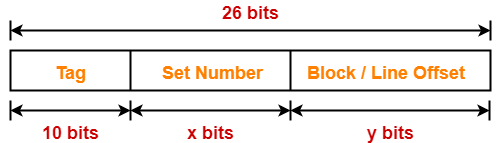
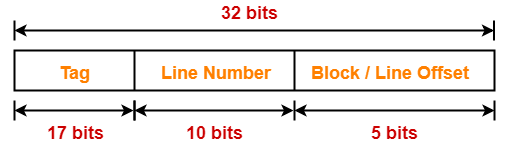
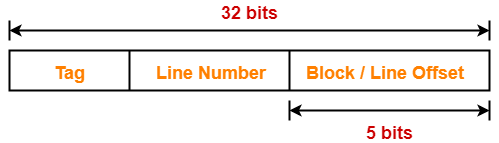
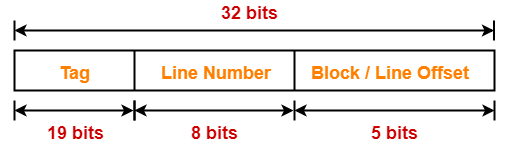
Result-02: Effect of Changing Block Size On Cache Tag in Direct Mapped Cache-

In direct mapped cache, block size does not affect the cache tag anyhow.

Explanation-

Keeping the cache size constant, we have-

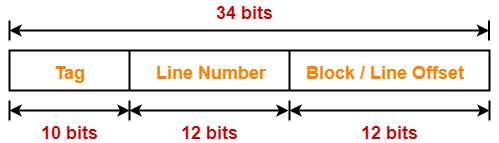
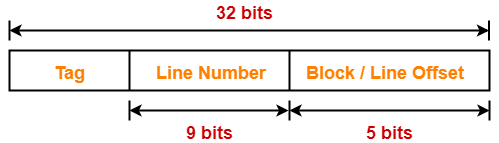
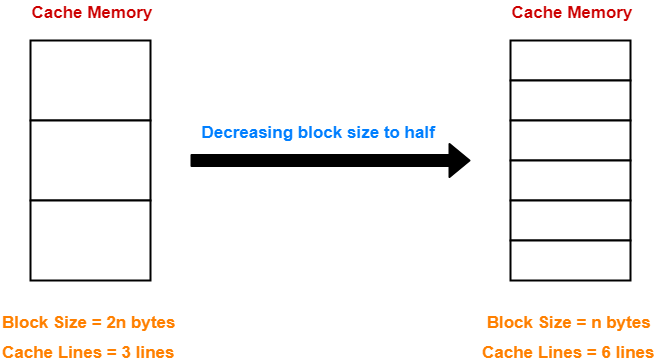
Case-01: Decreasing the Block Size-

Decreasing the block size increases the number of lines in cache.
With the decrease in block size, the number of bits in block offset decreases.
However, with the increase in the number of cache lines, number of bits in line number increases.
So, number of bits in line number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

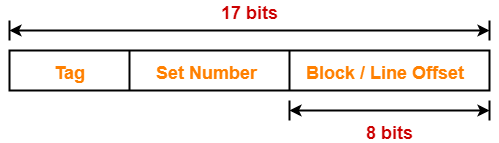
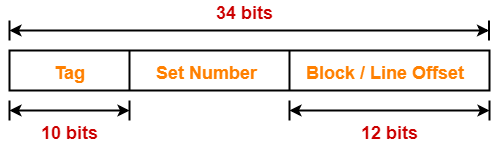
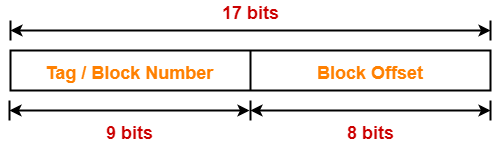
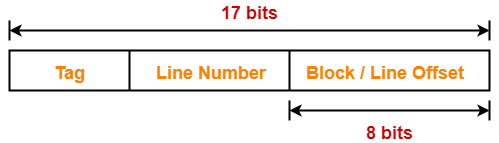
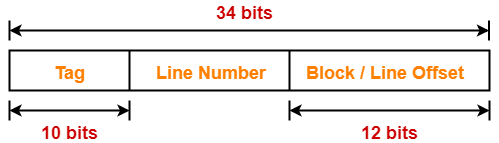
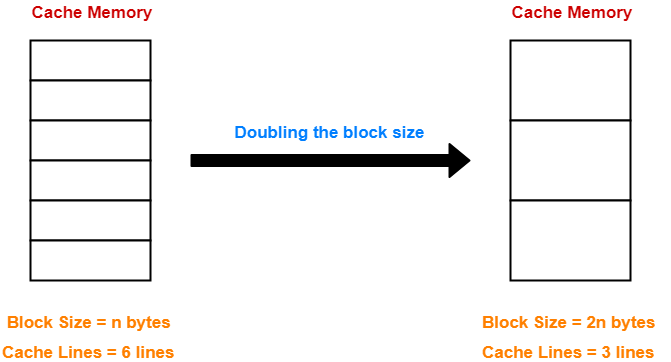
Example-

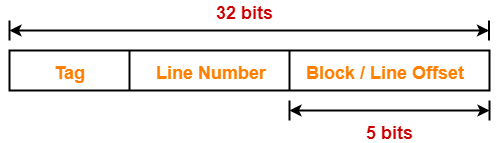
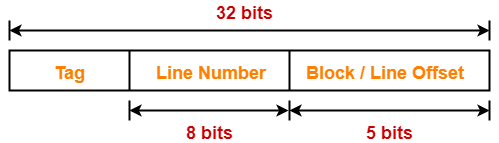
Case-02: Increasing the Block Size-

Increasing the block size decreases the number of lines in cache.
With the increase in block size, the number of bits in block offset increases.
However, with the decrease in the number of cache lines, number of bits in line number decreases.
Thus, number of bits in line number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

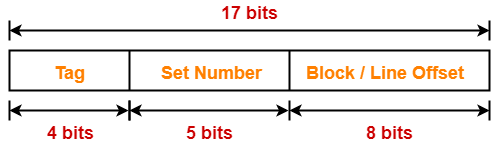
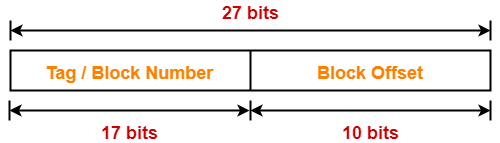
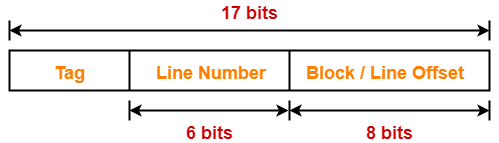
Example-

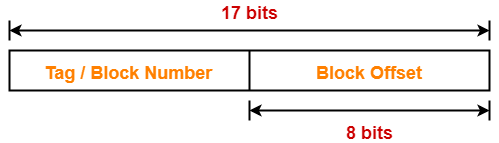
Result-03: Effect of Changing Block Size On Cache Tag in Fully Associative Cache-

In fully associative cache, on decreasing block size, cache tag is reduced and vice versa.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

Decreasing the block size decreases the number of bits in block offset.
With the decrease in number of bits in block offset, number of bits in tag increases.

Case-02: Increasing the Block Size-

Increasing the block size increases the number of bits in block offset.
With the increase in number of bits in block offset, number of bits in tag decreases.

Result-04: Effect of Changing Block Size On Cache Tag in Set Associative Cache-

In set associative cache, block size does not affect cache tag anyhow.

Explanation-

Keeping the cache size constant, we have-

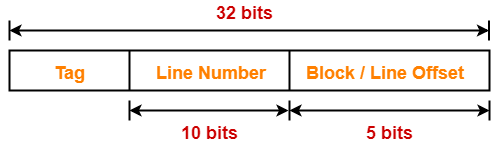
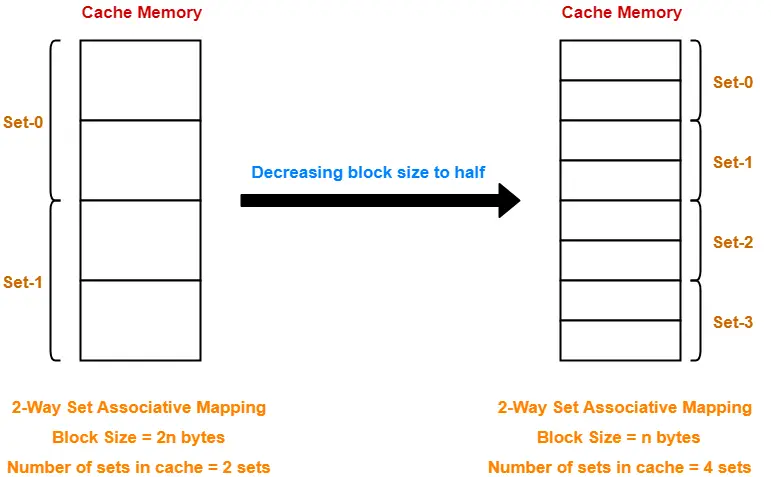
Case-01: Decreasing the Block Size-

Decreasing the block size increases the number of lines in cache.
With the decrease in block size, number of bits in block offset decreases.
With the increase in the number of cache lines, number of sets in cache increases.
With the increase in number of sets in cache, number of bits in set number increases.
So, number of bits in set number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

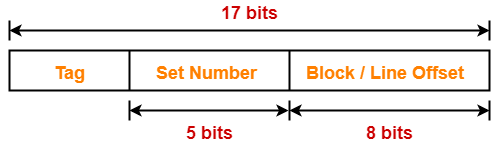
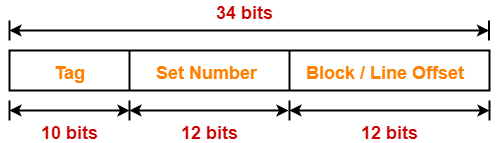
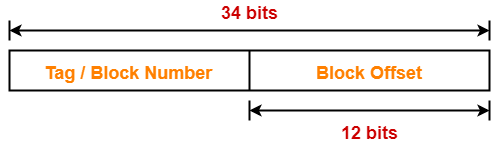
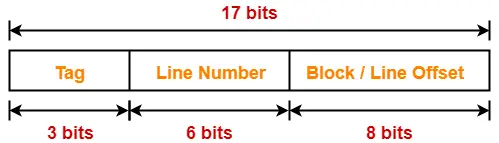
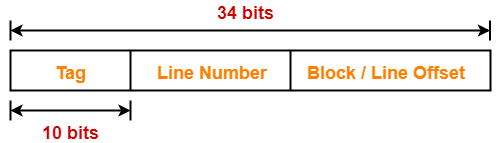
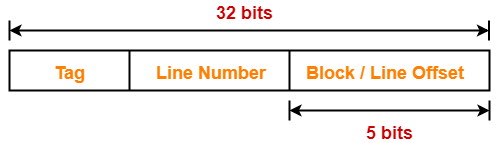
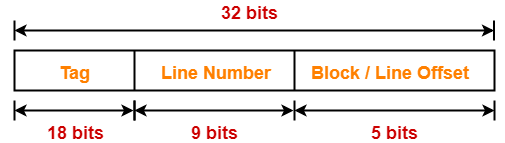
Example-

Case-02: Increasing the Block Size-

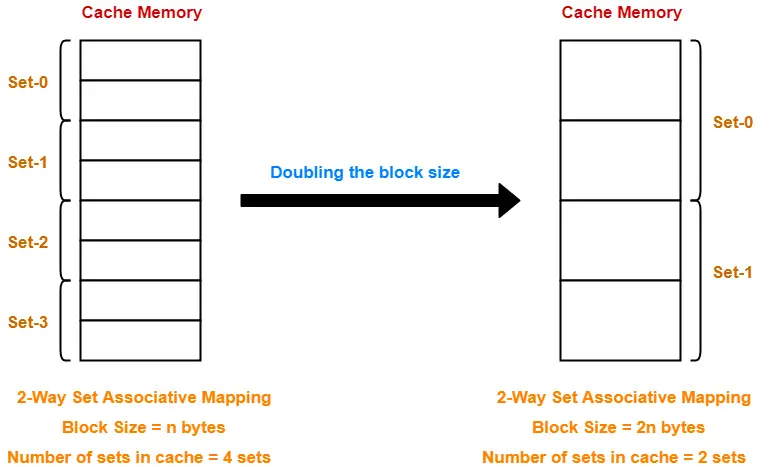
Increasing the block size decreases the number of lines in cache.
With the increase in block size, number of bits in block offset increases.
With the decrease in the number of cache lines, number of sets in cache decreases.
With the decrease in number of sets in cache, number of bits in set number decreases.
So, number of bits in set number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

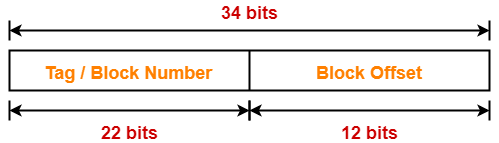
Example-

Result-05: Effect of Changing Block Size On Cache Miss Penalty-

A smaller cache block incurs a lower cache miss penalty.

Explanation-

When a cache miss occurs, block containing the required word has to be brought from the main memory.
If the block size is small, then time taken to bring the block in the cache will be less.
Hence, less miss penalty will incur.
But if the block size is large, then time taken to bring the block in the cache will be more.
Hence, more miss penalty will incur.

Result-06: Effect of Cache Tag On Cache Hit Time-

A smaller cache tag ensures a lower cache hit time.

Explanation-

Cache hit time is the time required to find out whether the required block is in cache or not.
It involves comparing the tag of generated address with the tag of cache lines.
Smaller is the cache tag, lesser will be the time taken to perform the comparisons.
Hence, smaller cache tag ensures lower cache hit time.
On the other hand, larger is the cache tag, more will be time taken to perform the comparisons.
Thus, larger cache tag results in higher cache hit time.

PRACTICE PROBLEM BASED ON CACHE LINE-

Problem-

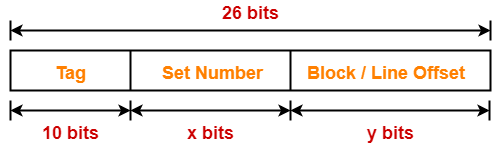
In designing a computer’s cache system, the cache block or cache line size is an important parameter. Which of the following statements is correct in this context?

A smaller block size implies better spatial locality
A smaller block size implies a smaller cache tag and hence lower cache tag overhead
A smaller block size implies a larger cache tag and hence lower cache hit time
A smaller bock size incurs a lower cache miss penalty

Solution-

Option (D) is correct. (Result-05)

Reasons-

Option (A) is incorrect because-

Smaller block does not imply better spatial locality.
Always, Larger the block size, better is the spatial locality.

Option (B) is incorrect because-

In direct mapped cache and set associative cache, there is no effect of changing block size on cache tag.
In fully associative mapped cache, on decreasing block size, cache tag becomes larger.
Thus, smaller block size does not imply smaller cache tag in any cache organization.

Option (C) is incorrect because-

“A smaller block size implies a larger cache tag” is true only for fully associative mapped cache.
Larger cache tag does not imply lower cache hit time rather cache hit time is increased.

Next Article- Magnetic Disk | Important Formulas

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Set Associative Mapping | Practice Problems

Computer Organization and Architecture

Set Associative Mapping-

Before you go through this article, make sure that you have gone through the previous article on Set Associative Mapping.

In set associative mapping,

A particular block of main memory can be mapped to one particular cache set only.
Block ‘j’ of main memory will map to set number (j mod number of sets in cache) of the cache.
A replacement algorithm is needed if the cache is full.

In this article, we will discuss practice problems based on set associative mapping.

Also Read- Cache Mapping Techniques

PRACTICE PROBLEMS BASED ON SET ASSOCIATIVE MAPPING-

Problem-01:

Consider a 2-way set associative mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

Number of bits in tag
Tag directory size

Solution-

Given-

Set size = 2
Cache memory size = 16 KB
Block size = Frame size = Line size = 256 bytes
Main memory size = 128 KB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

Thus, Number of bits in physical address = 17 bits

Number of Bits in Block Offset-

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 64 lines

Thus, Number of lines in cache = 64 lines

Number of Sets in Cache-

Total number of sets in cache

= Total number of lines in cache / Set size

= 64 / 2

= 32 sets

= 2⁵ sets

Thus, Number of bits in set number = 5 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – (Number of bits in set number + Number of bits in block offset)

= 17 bits – (5 bits + 8 bits)

= 17 bits – 13 bits

= 4 bits

Thus, Number of bits in tag = 4 bits

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 64 x 4 bits

= 256 bits

= 32 bytes

Thus, size of tag directory = 32 bytes

Also Read- Practice Problems On Direct Mapping

Problem-02:

Consider a 8-way set associative mapped cache of size 512 KB with block size 1 KB. There are 7 bits in the tag. Find-

Size of main memory
Tag directory size

Solution-

Given-

Set size = 8
Cache memory size = 512 KB
Block size = Frame size = Line size = 1 KB
Number of bits in tag = 7 bits

We consider that the memory is byte addressable.

Number of Bits in Block Offset-

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 512 lines

Thus, Number of lines in cache = 512 lines

Number of Sets in Cache-

Total number of sets in cache

= Total number of lines in cache / Set size

= 512 / 8

= 64 sets

= 2⁶ sets

Thus, Number of bits in set number = 6 bits

Number of Bits in Physical Address-

Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

= 7 bits + 6 bits + 10 bits

= 23 bits

Thus, Number of bits in physical address = 23 bits

Size of Main Memory-

We have,

Number of bits in physical address = 23 bits

Thus, Size of main memory

= 2²³ bytes

= 8 MB

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 512 x 7 bits

= 3584 bits

= 448 bytes

Thus, size of tag directory = 448 bytes

Problem-03:

Consider a 4-way set associative mapped cache with block size 4 KB. The size of main memory is 16 GB and there are 10 bits in the tag. Find-

Size of cache memory
Tag directory size

Solution-

Given-

Set size = 4
Block size = Frame size = Line size = 4 KB
Main memory size = 16 GB
Number of bits in tag = 10 bits

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

Number of Bits in Block Offset-

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

Number of Bits in Set Number-

Number of bits in set number

= Number of bits in physical address – (Number of bits in tag + Number of bits in block offset)

= 34 bits – (10 bits + 12 bits)

= 34 bits – 22 bits

= 12 bits

Thus, Number of bits in set number = 12 bits

Number of Sets in Cache-

We have-

Number of bits in set number = 12 bits

Thus, Total number of sets in cache = 2¹² sets

Number of Lines in Cache-

We have-

Total number of sets in cache = 2¹² sets

Each set contains 4 lines

Thus,

Total number of lines in cache

= Total number of sets in cache x Number of lines in each set

= 2¹² x 4 lines

= 2¹⁴ lines

Size of Cache Memory-

Size of cache memory

= Total number of lines in cache x Line size

= 2¹⁴ x 4 KB

= 2¹⁶ KB

= 64 MB

Thus, Size of cache memory = 64 MB

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2¹⁴ x 10 bits

= 163840 bits

= 20480 bytes

= 20 KB

Thus, size of tag directory = 20 KB

Also Read- Practice Problems On Fully Associative Mapping

Problem-04:

Consider a 8-way set associative mapped cache. The size of cache memory is 512 KB and there are 10 bits in the tag. Find the size of main memory.

Solution-

Given-

Set size = 8
Cache memory size = 512 KB
Number of bits in tag = 10 bits

We consider that the memory is byte addressable.

Let-

Number of bits in set number field = x bits
Number of bits in block offset field = y bits

Sum of Number Of Bits Of Set Number Field And Block Offset Field-

We have,

Cache memory size = Number of sets in cache x Number of lines in one set x Line size

Now, substituting the values, we get-

512 KB = 2^x x 8 x 2^y bytes

2¹⁹ bytes = 2^3+x+y bytes

19 = 3 +x + y

x + y = 19 – 3

x + y = 16

Number of Bits in Physical Address-

Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

= 10 bits + x bits + y bits

= 10 bits + (x + y) bits

= 10 bits + 16 bits

= 26 bits

Thus, Number of bits in physical address = 26 bits

Size of Main Memory-

We have,

Number of bits in physical address = 26 bits

Thus, Size of main memory

= 2²⁶ bytes

= 64 MB

Thus, size of main memory = 64 MB

Problem-05:

Consider a 4-way set associative mapped cache. The size of main memory is 64 MB and there are 10 bits in the tag. Find the size of cache memory.

Solution-

Given-

Set size = 4
Main memory size = 64 MB
Number of bits in tag = 10 bits

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 64 MB

= 2²⁶ bytes

Thus, Number of bits in physical address = 26 bits

Sum Of Number Of Bits Of Set Number Field And Block Offset Field-

Let-

Number of bits in set number field = x bits
Number of bits in block offset field = y bits

Then, Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

So, we have-

26 bits = 10 bits + x bits + y bits

26 = 10 + (x + y)

x + y = 26 – 10

x + y = 16

Thus, Sum of number of bits of set number field and block offset field = 16 bits

Size of Cache Memory-

Cache memory size

= Number of sets in cache x Number of lines in one set x Line size

= 2^x x 4 x 2^y bytes

= 2^2+x+y bytes

= 2²⁺¹⁶ bytes

= 2¹⁸ bytes

= 256 KB

Thus, size of cache memory = 256 KB

To watch video solutions and practice more problems,

Watch this Video Lecture

Next Article- Miscellaneous Practice Problems On Cache Mapping Techniques

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Set Associative Mapping | Set Associative Cache

Computer Organization and Architecture

Cache Mapping-

Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.

Cache mapping is a technique by which the contents of main memory are brought into the cache memory.

Different cache mapping techniques are-

Direct Mapping
Fully Associative Mapping
K-way Set Associative Mapping

In this article, we will discuss about set associative mapping in detail.

Set Associative Mapping-

In k-way set associative mapping,

Cache lines are grouped into sets where each set contains k number of lines.
A particular block of main memory can map to only one particular set of the cache.
However, within that set, the memory block can map to any freely available cache line.
The set of the cache to which a particular block of the main memory can map is given by-

Cache set number

= ( Main Memory Block Address ) Modulo (Number of sets in Cache)

Division of Physical Address-

In set associative mapping, the physical address is divided as-

Set Associative Cache-

Set associative cache employs set associative cache mapping technique.

The following steps explain the working of set associative cache-

After CPU generates a memory request,

The set number field of the address is used to access the particular set of the cache.
The tag field of the CPU address is then compared with the tags of all k lines within that set.
If the CPU tag matches to the tag of any cache line, a cache hit occurs.
If the CPU tag does not match to the tag of any cache line, a cache miss occurs.
In case of a cache miss, the required word has to be brought from the main memory.
If the cache is full, a replacement is made in accordance with the employed replacement policy.

Implementation-

The following diagram shows the implementation of 2-way set associative cache-

(For simplicity, this diagram shows does not show all the lines of multiplexers)

The steps involved are as follows-

Step-01:

Each multiplexer reads the set number from the generated physical address using its select lines in parallel.
To read the set number of S bits, number of select lines each multiplexer must have = S.

Step-02:

After reading the set number, each multiplexer goes to the corresponding set in the cache memory.
Then, each multiplexer goes to the lines of that set using its input lines in parallel.
Number of input lines each multiplexer must have = Number of lines in one set

Step-03:

Each multiplexer outputs the tag bit it has selected from the lines of selected set to the comparators using its output line.
Number of output line in each multiplexer = 1.

UNDERSTAND

It is important to understand-

A multiplexer can output only a single bit on output line.
So, to output one complete tag to the comparator,

Number of multiplexers required = Number of bits in the tag

If there are k lines in one set, then number of tags to output = k, thus-

Number of multiplexers required = Number of lines in one set (k) x Number of bits in the tag

Each multiplexer is configured to read the tag bit of specific line at specific location.
So, each multiplexer selects the tag bit for which it has been configured and outputs on the output line.
The complete tags as whole are sent to the comparators for comparison in parallel.

Step-04:

Comparators compare the tags coming from the multiplexers with the tag of the generated address.
This comparison takes place in parallel.
If there are k lines in one set (thus k tags), then-

Number of comparators required = k

and

Size of each comparator = Number of bits in the tag

The output result of each comparator is fed as an input to an OR Gate.
OR Gate is usually implemented using 2 x 1 multiplexer.
If the output of OR Gate is 1, a cache hit occurs otherwise a cache miss occurs.

Hit latency-

The time taken to find out whether the required word is present in the Cache Memory or not is called as hit latency.

For set associative mapping,

Hit latency = Multiplexer latency + Comparator latency + OR Gate latency

Also Read- Direct Mapped Cache | Implementation & Formulas

Important Results-

Following are the few important results for set associative cache-

Block j of main memory maps to set number (j mod number of sets in cache) of the cache.
Number of multiplexers required = Number of lines in one set (k) x Number of bits in tag
Size of each multiplexer = Number of lines in one set (k) x 1
Number of comparators required = Number of lines in one set (k)
Size of each comparator = Number of bits in the tag
Hit latency = Multiplexer latency + Comparator latency + OR Gate latency

To gain better understanding about set associative mapping,

Watch this Video Lecture

Next Article- Practice Problems On Set Associative Mapping

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Fully Associative Mapping | Practice Problems

Computer Organization and Architecture

Fully Associative Mapping-

Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.

In fully associative mapping,

A block of main memory can be mapped to any freely available cache line.
This makes fully associative mapping more flexible than direct mapping.
A replacement algorithm is needed to replace a block if the cache is full.

In this article, we will discuss practice problems based on fully associative mapping.

Also Read- Practice Problems On Direct Mapping

PRACTICE PROBLEMS BASED ON FULLY ASSOCIATIVE MAPPING-

Problem-01:

Consider a fully associative mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

Number of bits in tag
Tag directory size

Solution-

Given-

Cache memory size = 16 KB
Block size = Frame size = Line size = 256 bytes
Main memory size = 128 KB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

Thus, Number of bits in physical address = 17 bits

Number of Bits in Block Offset-

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 17 bits – 8 bits

= 9 bits

Thus, Number of bits in tag = 9 bits

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 2⁶ lines

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁶ x 9 bits

= 576 bits

= 72 bytes

Thus, size of tag directory = 72 bytes

Problem-02:

Consider a fully associative mapped cache of size 512 KB with block size 1 KB. There are 17 bits in the tag. Find-

Size of main memory
Tag directory size

Solution-

Given-

Cache memory size = 512 KB
Block size = Frame size = Line size = 1 KB
Number of bits in tag = 17 bits

We consider that the memory is byte addressable.

Number of Bits in Block Offset-

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

Number of Bits in Physical Address-

Number of bits in physical address

= Number of bits in tag + Number of bits in block offset

= 17 bits + 10 bits

= 27 bits

Thus, Number of bits in physical address = 27 bits

Size of Main Memory-

We have,

Number of bits in physical address = 27 bits

Thus, Size of main memory

= 2²⁷ bytes

= 128 MB

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 512 lines

= 2⁹ lines

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁹ x 17 bits

= 8704 bits

= 1088 bytes

Thus, size of tag directory = 1088 bytes

Also Read- Practice Problems On Set Associative Mapping

Problem-03:

Consider a fully associative mapped cache with block size 4 KB. The size of main memory is 16 GB. Find the number of bits in tag.

Solution-

Given-

Block size = Frame size = Line size = 4 KB
Size of main memory = 16 GB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

Number of Bits in Block Offset-

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 34 bits – 12 bits

= 22 bits

Thus, Number of bits in tag = 22 bits

To watch video solutions and practice more problems,

Watch this Video Lecture

Next Article- Set Associative Mapping | Implementation & Formulas

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Direct Mapping | Cache | Practice Problems

Computer Organization and Architecture

Direct Mapping-

Before you go through this article, make sure that you have gone through the previous article on Direct Mapping.

In direct mapping,

A particular block of main memory can be mapped to one particular cache line only.
Block ‘j’ of main memory will map to line number (j mod number of cache lines) of the cache.
There is no need of any replacement algorithm.

In this article, we will discuss practice problems based on direct mapping.

Also Read- Cache Mapping Techniques

PRACTICE PROBLEMS BASED ON DIRECT MAPPING-

Problem-01:

Consider a direct mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

Number of bits in tag
Tag directory size

Solution-

Given-

Cache memory size = 16 KB
Block size = Frame size = Line size = 256 bytes
Main memory size = 128 KB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

Thus, Number of bits in physical address = 17 bits

Number of Bits in Block Offset-

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

Number of Bits in Line Number-

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 2⁶ lines

Thus, Number of bits in line number = 6 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 17 bits – (6 bits + 8 bits)

= 17 bits – 14 bits

= 3 bits

Thus, Number of bits in tag = 3 bits

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁶ x 3 bits

= 192 bits

= 24 bytes

Thus, size of tag directory = 24 bytes

Problem-02:

Consider a direct mapped cache of size 512 KB with block size 1 KB. There are 7 bits in the tag. Find-

Size of main memory
Tag directory size

Solution-

Given-

Cache memory size = 512 KB
Block size = Frame size = Line size = 1 KB
Number of bits in tag = 7 bits

We consider that the memory is byte addressable.

Number of Bits in Block Offset-

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

Number of Bits in Line Number-

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 2⁹ lines

Thus, Number of bits in line number = 9 bits

Number of Bits in Physical Address-

Number of bits in physical address

= Number of bits in tag + Number of bits in line number + Number of bits in block offset

= 7 bits + 9 bits + 10 bits

= 26 bits

Thus, Number of bits in physical address = 26 bits

Size of Main Memory-

We have,

Number of bits in physical address = 26 bits

Thus, Size of main memory

= 2²⁶ bytes

= 64 MB

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁹ x 7 bits

= 3584 bits

= 448 bytes

Thus, size of tag directory = 448 bytes

Problem-03:

Consider a direct mapped cache with block size 4 KB. The size of main memory is 16 GB and there are 10 bits in the tag. Find-

Size of cache memory
Tag directory size

Solution-

Given-

Block size = Frame size = Line size = 4 KB
Size of main memory = 16 GB
Number of bits in tag = 10 bits

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

Number of Bits in Block Offset-

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

Number of Bits in Line Number-

Number of bits in line number

= Number of bits in physical address – (Number of bits in tag + Number of bits in block offset)

= 34 bits – (10 bits + 12 bits)

= 34 bits – 22 bits

= 12 bits

Thus, Number of bits in line number = 12 bits

Number of Lines in Cache-

We have-

Number of bits in line number = 12 bits

Thus, Total number of lines in cache = 2¹² lines

Size of Cache Memory-

Size of cache memory

= Total number of lines in cache x Line size

= 2¹² x 4 KB

= 2¹⁴ KB

= 16 MB

Thus, Size of cache memory = 16 MB

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2¹² x 10 bits

= 40960 bits

= 5120 bytes

Thus, size of tag directory = 5120 bytes

Also Read- Practice Problems On Set Associative Mapping

Problem-04:

Consider a direct mapped cache of size 32 KB with block size 32 bytes. The CPU generates 32 bit addresses. The number of bits needed for cache indexing and the number of tag bits are respectively-

10, 17
10, 22
15, 17
5, 17

Solution-

Given-

Cache memory size = 32 KB
Block size = Frame size = Line size = 32 bytes
Number of bits in physical address = 32 bits

Number of Bits in Block Offset-

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

Number of Bits in Line Number-

Total number of lines in cache

= Cache size / Line size

= 32 KB / 32 bytes

= 2¹⁰ lines

Thus, Number of bits in line number = 10 bits

Number of Bits Required For Cache Indexing-

Number of bits required for cache indexing

= Number of bits in line number

= 10 bits

Number Of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (10 bits + 5 bits)

= 32 bits – 15 bits

= 17 bits

Thus, Number of bits in tag = 17 bits

Thus, Option (A) is correct.

Problem-05:

Consider a machine with a byte addressable main memory of 2³² bytes divided into blocks of size 32 bytes. Assume that a direct mapped cache having 512 cache lines is used with this machine. The size of the tag field in bits is ______.

Solution-

Given-

Main memory size = 2³² bytes
Block size = Frame size = Line size = 32 bytes
Number of lines in cache = 512 lines

Number of Bits in Physical Address-

We have,

Size of main memory

= 2³² bytes

Thus, Number of bits in physical address = 32 bits

Number of Bits in Block Offset-

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

Number of Bits in Line Number-

Total number of lines in cache

= 512 lines

= 2⁹ lines

Thus, Number of bits in line number = 9 bits

Number Of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (9 bits + 5 bits)

= 32 bits – 14 bits

= 18 bits

Thus, Number of bits in tag = 18 bits

Problem-06:

An 8 KB direct-mapped write back cache is organized as multiple blocks, each of size 32 bytes. The processor generates 32 bit addresses. The cache controller maintains the tag information for each cache block comprising of the following-

1 valid bit
1 modified bit
As many bits as the minimum needed to identify the memory block mapped in the cache

What is the total size of memory needed at the cache controller to store meta data (tags) for the cache?

4864 bits
6144 bits
6656 bits
5376 bits

Solution-

Given-

Cache memory size = 8 KB
Block size = Frame size = Line size = 32 bytes
Number of bits in physical address = 32 bits

Number of Bits in Block Offset-

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

Number of Bits in Line Number-

Total number of lines in cache

= Cache memory size / Line size

= 8 KB / 32 bytes

= 2¹³ bytes / 2⁵ bytes

= 2⁸ lines

Thus, Number of bits in line number = 8 bits

Number Of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (8 bits + 5 bits)

= 32 bits – 13 bits

= 19 bits

Thus, Number of bits in tag = 19 bits

Memory Size Needed At Cache Controller-

Size of memory needed at cache controller

= Number of lines in cache x (1 valid bit + 1 modified bit + 19 bits to identify block)

= 2⁸ x 21 bits

= 5376 bits

To watch video solutions and practice more problems,

Watch this Video Lecture

Next Article- Practice Problems On Fully Associative Mapping

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

← Older Posts

Newer Posts →