Cache Mapping-
Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.
We have discussed-
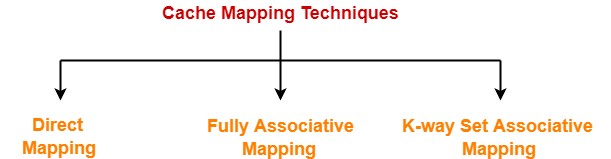
- Cache mapping is a technique by which the contents of main memory are brought into the cache.
- Cache mapping is performed using following three different techniques-
In this article, we will discuss practice problems based on cache mapping techniques.
PRACTICE PROBLEMS BASED ON CACHE MAPPING TECHNIQUES-
Problem-01:
The main memory of a computer has 2 cm blocks while the cache has 2c blocks. If the cache uses the set associative mapping scheme with 2 blocks per set, then block k of the main memory maps to the set-
- (k mod m) of the cache
- (k mod c) of the cache
- (k mod 2 c) of the cache
- (k mod 2 cm) of the cache
Solution-
Given-
- Number of blocks in main memory = 2 cm
- Number of blocks in cache = 2 c
- Number of blocks in one set of cache = 2
Number of Sets in Cache-
Number of sets in cache
= Number of blocks in cache / Number of blocks in one set
= 2 c / 2
= c
Required Mapping-
In set associative mapping,
- Block ‘j’ of main memory maps to set number (j modulo number of sets in cache) of the cache.
- So, block ‘k’ of main memory maps to set number (k mod c) of the cache.
- Thus, option (B) is correct.
Also Read- Practice Problems On Direct Mapping
Problem-02:
In a k-way set associative cache, the cache is divided into v sets, each of which consists of k lines. The lines of a set placed in sequence one after another. The lines in set s are sequenced before the lines in set (s+1). The main memory blocks are numbered 0 on wards. The main memory block numbered ‘j’ must be mapped to any one of the cache lines from-
- (j mod v) x k to (j mod v) x k + (k – 1)
- (j mod v) to (j mod v) + (k – 1)
- (j mod k) to (j mod k) + (v – 1)
- (j mod k) x v to (j mod k) x v + (v – 1)
Solution-
Let-
- 2-way set associative mapping is used, then k = 2
- Number of sets in cache = 4, then v = 4
- Block number ‘3’ has to be mapped, then j = 3
The given options on substituting these values reduce to-
- (3 mod 4) x 2 to (3 mod 4) x 2 + (2 – 1) = 6 to 7
- (3 mod 4) to (3 mod 4) + (2 – 1) = 3 to 4
- (3 mod 2) to (3 mod 2) + (4 – 1) = 1 to 4
- (3 mod 2) x 4 to (3 mod 2) x 4 + (4 – 1) = 4 to 7
Now, we have been asked to what range of cache lines, block number 3 can be mapped.
According to the above data, the cache memory and main memory will look like-
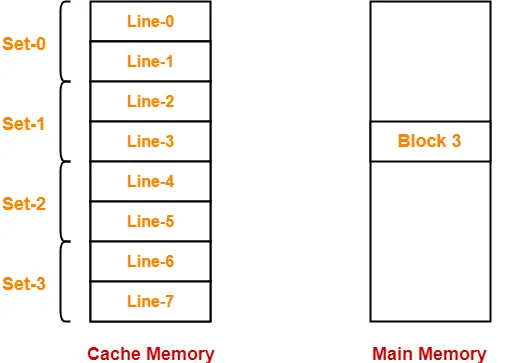
In set associative mapping,
- Block ‘j’ of main memory maps to set number (j modulo number of sets in cache) of the cache.
- So, block 3 of main memory maps to set number (3 mod 4) = 3 of cache.
- Within set number 3, block 3 can be mapped to any of the cache lines.
- Thus, block 3 can be mapped to cache lines ranging from 6 to 7.
Thus, Option (A) is correct.
Problem-03:
A block-set associative cache memory consists of 128 blocks divided into four block sets . The main memory consists of 16,384 blocks and each block contains 256 eight bit words.
- How many bits are required for addressing the main memory?
- How many bits are needed to represent the TAG, SET and WORD fields?
Solution-
Given-
- Number of blocks in cache memory = 128
- Number of blocks in each set of cache = 4
- Main memory size = 16384 blocks
- Block size = 256 bytes
- 1 word = 8 bits = 1 byte
Main Memory Size-
We have-
Size of main memory
= 16384 blocks
= 16384 x 256 bytes
= 222 bytes
Thus, Number of bits required to address main memory = 22 bits
Number of Bits in Block Offset-
We have-
Block size
= 256 bytes
= 28 bytes
Thus, Number of bits in block offset or word = 8 bits
Number of Bits in Set Number-
Number of sets in cache
= Number of lines in cache / Set size
= 128 blocks / 4 blocks
= 32 sets
= 25 sets
Thus, Number of bits in set number = 5 bits
Number of Bits in Tag Number-
Number of bits in tag
= Number of bits in physical address – (Number of bits in set number + Number of bits in word)
= 22 bits – (5 bits + 8 bits)
= 22 bits – 13 bits
= 9 bits
Thus, Number of bits in tag = 9 bits
Thus, physical address is-
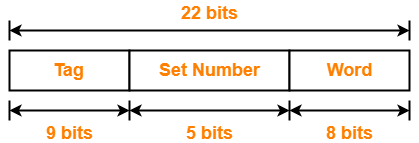
Problem-04:
A computer has a 256 KB, 4-way set associative, write back data cache with block size of 32 bytes. The processor sends 32 bit addresses to the cache controller. Each cache tag directory entry contains in addition to address tag, 2 valid bits, 1 modified bit and 1 replacement bit.
Part-01:
The number of bits in the tag field of an address is-
- 11
- 14
- 16
- 27
Part-02:
The size of the cache tag directory is-
- 160 Kbits
- 136 Kbits
- 40 Kbits
- 32 Kbits
Solution-
Given-
- Cache memory size = 256 KB
- Set size = 4 blocks
- Block size = 32 bytes
- Number of bits in physical address = 32 bits
Number of Bits in Block Offset-
We have-
Block size
= 32 bytes
= 25 bytes
Thus, Number of bits in block offset = 5 bits
Number of Lines in Cache-
Number of lines in cache
= Cache size / Line size
= 256 KB / 32 bytes
= 218 bytes / 25 bytes
= 213 lines
Thus, Number of lines in cache = 213 lines
Number of Sets in Cache-
Number of sets in cache
= Number of lines in cache / Set size
= 213 lines / 22 lines
= 211 sets
Thus, Number of bits in set number = 11 bits
Number of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in set number + Number of bits in block offset)
= 32 bits – (11 bits + 5 bits)
= 32 bits – 16 bits
= 16 bits
Thus, Number of bits in tag = 16 bits
Tag Directory Size-
Size of tag directory
= Number of lines in cache x Size of tag
= 213 x (16 bits + 2 valid bits + 1 modified bit + 1 replacement bit)
= 213 x 20 bits
= 163840 bits
= 20 KB or 160 Kbits
Thus,
- For part-01, Option (C) is correct.
- For part-02, Option (A) is correct.
Also Read- Practice Problems On Fully Associative Mapping
Problem-05:
A 4-way set associative cache memory unit with a capacity of 16 KB is built using a block size of 8 words. The word length is 32 bits. The size of the physical address space is 4 GB. The number of bits for the TAG field is _____.
Solution-
Given-
- Set size = 4 lines
- Cache memory size = 16 KB
- Block size = 8 words
- 1 word = 32 bits = 4 bytes
- Main memory size = 4 GB
Number of Bits in Physical Address-
We have,
Main memory size
= 4 GB
= 232 bytes
Thus, Number of bits in physical address = 32 bits
Number of Bits in Block Offset-
We have,
Block size
= 8 words
= 8 x 4 bytes
= 32 bytes
= 25 bytes
Thus, Number of bits in block offset = 5 bits
Number of Lines in Cache-
Number of lines in cache
= Cache size / Line size
= 16 KB / 32 bytes
= 214 bytes / 25 bytes
= 29 lines
= 512 lines
Thus, Number of lines in cache = 512 lines
Number of Sets in Cache-
Number of sets in cache
= Number of lines in cache / Set size
= 512 lines / 4 lines
= 29 lines / 22 lines
= 27 sets
Thus, Number of bits in set number = 7 bits
Number of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in set number + Number of bits in block offset)
= 32 bits – (7 bits + 5 bits)
= 32 bits – 12 bits
= 20 bits
Thus, number of bits in tag = 20 bits
Problem-06:
If the associativity of a processor cache is doubled while keeping the capacity and block size unchanged, which one of the following is guaranteed to be NOT affected?
- Width of tag comparator
- Width of set index decoder
- Width of way selection multiplexer
- Width of processor to main memory data bus
Solution-
Since block size is unchanged, so number of bits in block offset will remain unchanged.
Effect On Width Of Tag Comparator-
- Associativity of cache is doubled means number of lines in one set is doubled.
- Since number of lines in one set is doubled, therefore number of sets reduces to half.
- Since number of sets reduces to half, so number of bits in set number decrements by 1.
- Since number of bits in set number decrements by 1, so number of bits in tag increments by 1.
- Since number of bits in tag increases, therefore width of tag comparator also increases.
Effect On Width of Set Index Decoder-
- Associativity of cache is doubled means number of lines in one set is doubled.
- Since number of lines in one set is doubled, therefore number of sets reduces to half.
- Since number of sets reduces to half, so number of bits in set number decrements by 1.
- Since number of bits in set number decreases, therefore width of set index decoder also decreases.
Effect On Width Of Way Selection Multiplexer-
- Associativity of cache (k) is doubled means number of lines in one set is doubled.
- New associativity of cache is 2k.
- To handle new associativity, size of multiplexers must be 2k x 1.
- Therefore, width of way selection multiplexer increases.
Effect On Width Of Processor To Main Memory Data Bus-
- Processor to main memory data bus has nothing to do with cache associativity.
- It depends on the number of bits in block offset which is unchanged here.
- So, width of processor to main memory data bus is not affected and remains unchanged.
Thus, Option (D) is correct.
Problem-07:
Consider a direct mapped cache with 8 cache blocks (0-7). If the memory block requests are in the order-
3, 5, 2, 8, 0, 6, 3, 9, 16, 20, 17, 25, 18, 30, 24, 2, 63, 5, 82, 17, 24
Which of the following memory blocks will not be in the cache at the end of the sequence?
- 3
- 18
- 20
- 30
Also, calculate the hit ratio and miss ratio.
Solution-
We have,
- There are 8 blocks in cache memory numbered from 0 to 7.
- In direct mapping, a particular block of main memory is mapped to a particular line of cache memory.
- The line number is given by-
Cache line number = Block address modulo Number of lines in cache
For the given sequence-
- Requests for memory blocks are generated one by one.
- The line number of the block is calculated using the above relation.
- Then, the block is placed in that particular line.
- If already there exists another block in that line, then it is replaced.
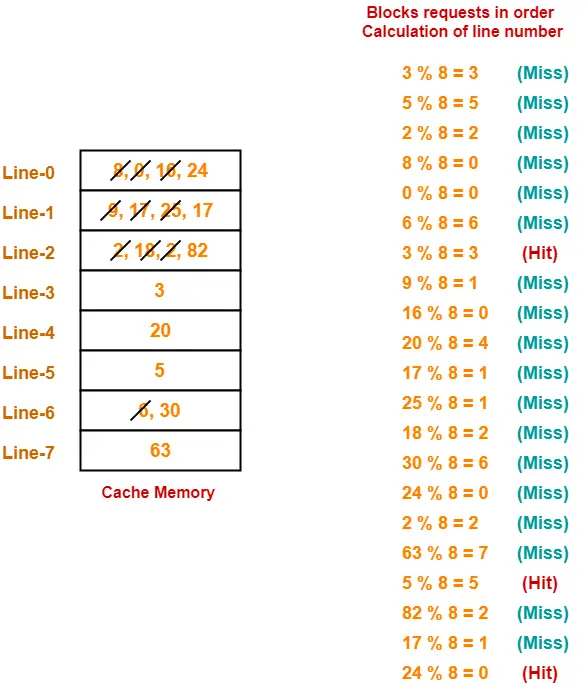
Thus,
- Out of given options, only block-18 is not present in the main memory.
- Option-(B) is correct.
- Hit ratio = 3 / 20
- Miss ratio = 17 / 20
Problem-08:
Consider a fully associative cache with 8 cache blocks (0-7). The memory block requests are in the order-
4, 3, 25, 8, 19, 6, 25, 8, 16, 35, 45, 22, 8, 3, 16, 25, 7
If LRU replacement policy is used, which cache block will have memory block 7?
Also, calculate the hit ratio and miss ratio.
Solution-
We have,
- There are 8 blocks in cache memory numbered from 0 to 7.
- In fully associative mapping, any block of main memory can be mapped to any line of the cache that is freely available.
- If all the cache lines are already occupied, then a block is replaced in accordance with the replacement policy.
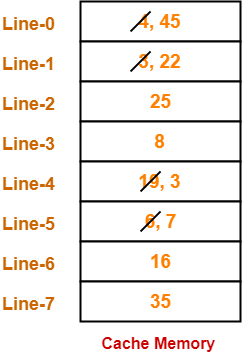
Thus,
- Line-5 contains the block-7.
- Hit ratio = 5 / 17
- Miss ratio = 12 / 17
Problem-09:
Consider a 4-way set associative mapping with 16 cache blocks. The memory block requests are in the order-
0, 255, 1, 4, 3, 8, 133, 159, 216, 129, 63, 8, 48, 32, 73, 92, 155
If LRU replacement policy is used, which cache block will not be present in the cache?
- 3
- 8
- 129
- 216
Also, calculate the hit ratio and miss ratio.
Solution-
We have,
- There are 16 blocks in cache memory numbered from 0 to 15.
- Each set contains 4 cache lines.
- In set associative mapping, a particular block of main memory is mapped to a particular set of cache memory.
- The set number is given by-
Cache line number = Block address modulo Number of sets in cache
For the given sequence-
- Requests for memory blocks are generated one by one.
- The set number of the block is calculated using the above relation.
- Within that set, the block is placed in any freely available cache line.
- If all the blocks are already occupied, then one of the block is replaced in accordance with the employed replacement policy.
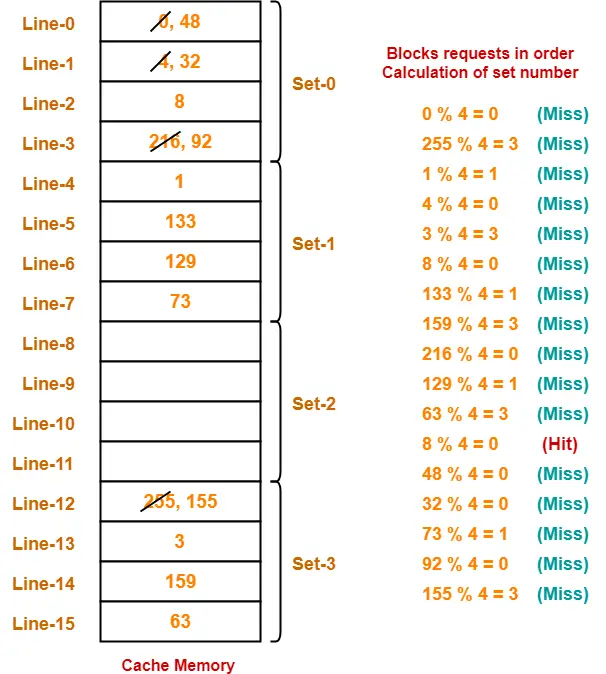
Thus,
- Out of given options, only block-216 is not present in the main memory.
- Option-(D) is correct.
- Hit ratio = 1 / 17
- Miss ratio = 16 / 17
Also Read- Practice Problems On Set Associative Mapping
Problem-10:
Consider a small 2-way set associative mapping with a total of 4 blocks. LRU replacement policy is used for choosing the block to be replaced. The number of cache misses for the following sequence of block addresses 8, 12, 0, 12, 8 is ____.
Solution-
- Practice yourself.
- Total number of cache misses = 4
Problem-11:
Consider the cache has 4 blocks. For the memory references-
5, 12, 13, 17, 4, 12, 13, 17, 2, 13, 19, 13, 43, 61, 19
What is the hit ratio for the following cache replacement algorithms-
- FIFO
- LRU
- Direct mapping
- 2-way set associative mapping using LRU
Solution-
- Practice yourself.
- Using FIFO as cache replacement algorithm, hit ratio = 5/15 = 1/3.
- Using LRU as cache replacement algorithm, hit ratio = 6/15 = 2/5.
- Using direct mapping as cache replacement algorithm, hit ratio = 1/15.
- Using 2-way set associative mapping as cache replacement algorithm, hit ratio = 5/15 = 1/3
Problem-12:
A hierarchical memory system has the following specification, 20 MB main storage with access time of 300 ns, 256 bytes cache with access time of 50 ns, word size 4 bytes, page size 8 words. What will be the hit ratio if the page address trace of a program has the pattern 0, 1, 2, 3, 0, 1, 2, 4 following LRU page replacement technique?
Solution-
Given-
- Main memory size = 20 MB
- Main memory access time = 300 ns
- Cache memory size = 256 bytes
- Cache memory access time = 50 ns
- Word size = 4 bytes
- Page size = 8 words
Line Size-
We have,
Line size
= 8 words
= 8 x 4 bytes
= 32 bytes
Number of Lines in Cache-
Number of lines in cache
= Cache size / Line size
= 256 bytes / 32 bytes
= 8 lines
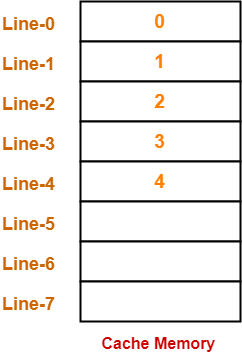
Thus,
- Number of hits = 3
- Hit ratio = 3 / 8
Problem-13:
Consider an array A[100] and each element occupies 4 words. A 32 word cache is used and divided into 8 word blocks. What is the hit ratio for the following code-
for (i=0 ; i < 100 ; i++)
A[i] = A[i] + 10;
Solution-
Number of lines in cache
= Cache size / Line size
= 32 words / 8 words
= 4 lines
Since each element of the array occupies 4 words, so-
Number of elements that can be placed in one line = 2
Now, let us analyze the statement-
A[i] = A[i] + 10;
For each i,
- Firstly, the value of A[i] is read.
- Secondly, 10 is added to the A[i].
- Thirdly, the updated value of A[i] is written back.
Thus,
- For each i, A[i] is accessed two times.
- Two memory accesses are required-one for read operation and other for write operation.
Assume the cache is all empty initially.
In the first loop iteration,
- First, value of A[0] has to be read.
- Since cache is empty, so A[0] is brought in the cache.
- Along with A[0], element A[1] also enters the cache since each block can hold 2 elements of the array.
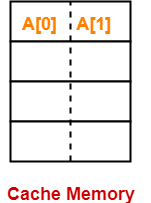
- Thus, For A[0], a miss occurred for the read operation.
- Now, 10 is added to the value of A[0].
- Now, the updated value has to be written back to A[0].
- Again cache memory is accessed to get A[0] for writing its updated value.
- This time, for A[0], a hit occurs for the write operation.
In the second loop iteration,
- First, value of A[1] has to be read.
- A[1] is already present in the cache.
- Thus, For A[1]. a hit occurs for the read operation.
- Now, 10 is added to the value of A[1].
- Now, the updated value has to be written back to A[1].
- Again cache memory is accessed to get A[1] for writing its updated value.
- Again, for A[1], a hit occurs for the write operation.
In the similar manner, for every next two consecutive elements-
- There will be a miss for the read operation for the first element.
- There will be a hit for the write operation for the first element.
- There will be a hit for both read and write operations for the second element.
Likewise, for 100 elements, we will have 50 such pairs in cache and in every pair, there will be one miss and three hits.
Thus,
- Total number of hits = 50 x 3 = 150
- Total number of misses = 50 x 1 = 50
- Total number of references = 200 (100 for read and 100 for write)
Thus,
- Hit ratio = 150 / 200 = 3 / 4 = 0.75
- Miss ratio = 50 / 200 = 1 / 4 = 0.25
Problem-14:
Consider an array has 100 elements and each element occupies 4 words. A 32 bit word cache is used and divided into a block of 8 words.
What is the hit ratio for the following statement-
for (i=0 ; i < 10 ; i++)
for (j=0 ; j < 10 ; j++)
A[i][j] = A[i][j] + 10;
if-
- Row major order is used
- Column major order is used
Solution-
According to question, cache is divided as-
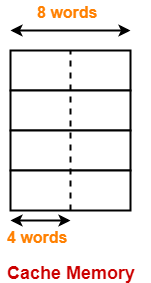
In each cache line, two elements of the array can reside.
Case-01: When Row Major Order is Used-
In row major order, elements of the array are stored row wise in the memory as-
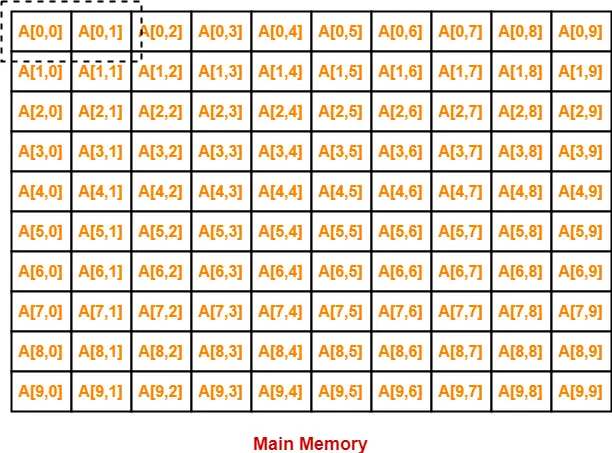
- In the first iteration, when A[0][0] will be brought in the cache, A[0][1] will also be brought.
- Then, things goes as it went in the previous question.
- There will be a miss for A[0,0] read operation and hit for A[0,0] write operation.
- For A[0,1], there will be a hit for both read and write operations.
- Similar will be the story with every next two consecutive elements.
Thus,
- Total number of hits = 50 x 3 = 150
- Total number of misses = 50 x 1 = 50
- Total number of references = 200 (100 for read and 100 for write)
Thus,
- Hit ratio = 150 / 200 = 3 / 4 = 0.75
- Miss ratio = 50 / 200 = 1 / 4 = 0.25
Case-02: When Column Major Order is Used-
In column major order, elements of the array are stored column wise in the memory as-
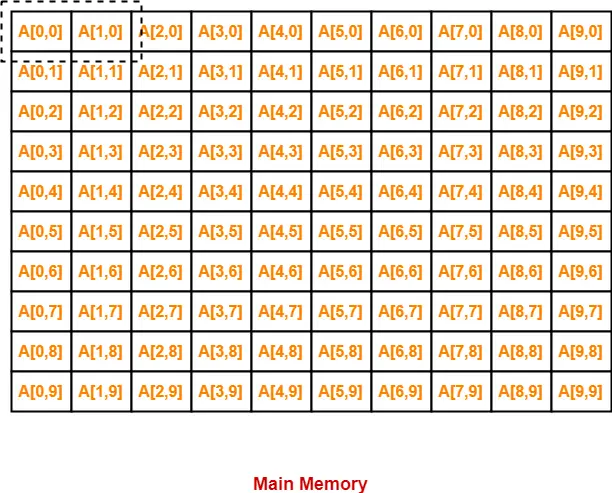
- In the first iteration, when A[0,0] will be brought in the cache, A[1][0] will also be brought.
- This time A[1][0] will not be useful in iteration-2.
- A[1][0] will be needed after surpassing 10 element.
- But by that time, this block would have got replaced since there are only 4 lines in the cache.
- For A[1][0] to be useful, there has to be at least 10 lines in the cache.
Thus,
Under given scenario, for each element of the array-
- There will be a miss for the read operation.
- There will be a hit for the write operation.
Thus,
- Total number of hits = 100 x 1 = 100
- Total number of misses = 100 x 1 = 100
- Total number of references = 200 (100 for read and 100 for write)
Thus,
- Hit ratio = 100 / 200 = 1 / 2 = 0.50
- Miss ratio = 100 / 200 = 1 / 2 = 0.50
To increase the hit rate, following measures can be taken-
- Row major order can be used (Hit rate = 75%)
- The statement A[i][j] = A[i][j] + 10 can be replaced with A[j,i] = A[j][i] + 10 (Hit rate = 75%)
Problem-15:
An access sequence of cache block addresses is of length N and contains n unique block addresses. The number of unique block addresses between two consecutive accesses to the same block address is bounded above by k. What is the miss ratio if the access sequence is passed through a cache of associativity A>=k exercising LRU replacement policy?
- n/N
- 1/N
- 1/A
- k/n
Solution-
Required miss ratio = n/N.
Thus, Option (A) is correct.
Next Article- Cache Line | Effects of Changing Cache Line Size
Get more notes and other study material of Computer Organization and Architecture.
Watch video lectures by visiting our YouTube channel LearnVidFun.