Grammar in Automata-

 

Before you go through this article, make sure that you have gone through the previous article on Types of Grammar in Automata.

 

On the basis of number of derivation trees, grammars are classified as-

 

 

1. Ambiguous Grammar
2. Unambiguous Grammar

 

1. Ambiguous Grammar-

 

A grammar is said to ambiguous if for any string generated by it, it produces more than one-

• Parse tree
• Or derivation tree
• Or syntax tree
• Or leftmost derivation
• Or rightmost derivation

 

Example-

 

Consider the following grammar-

E → E + E / E x E / id

Ambiguous Grammar

 

This grammar is an example of ambiguous grammar.

Any of the following reasons can be stated to prove the grammar ambiguous-

 

Reason-01:

 

Let us consider a string w generated by the grammar-

w = id + id x id

Now, let us draw the parse trees for this string w.

 

 

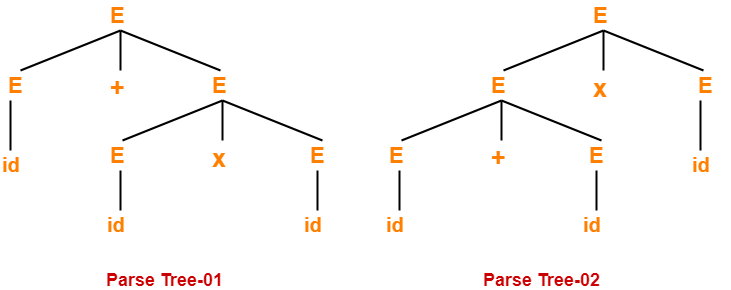
Since two parse trees exist for string w, therefore the grammar is ambiguous.

 

Reason-02:

 

Let us consider a string w generated by the grammar-

w = id + id x id

Now, let us draw the syntax trees for this string w.

 

 

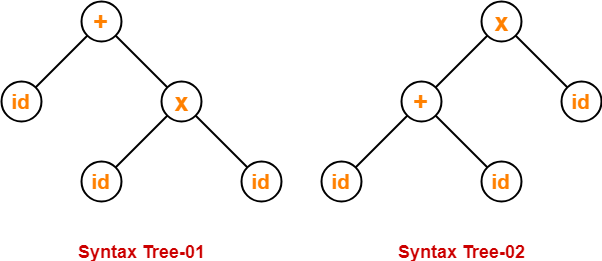
Since two syntax trees exist for string w, therefore the grammar is ambiguous.

 

Reason-03:

 

Let us consider a string w generated by the grammar-

w = id + id x id

Now, let us write the leftmost derivations for this string w.

 

 

Since two leftmost derivations exist for string w, therefore the grammar is ambiguous.

 

Reason-04:

 

Let us consider a string w generated by the grammar-

w = id + id x id

Now, let us write the rightmost derivations for this string w.

 

 

Since two rightmost derivations exist for string w, therefore the grammar is ambiguous.

 

Also Read- Checking Grammar Ambiguity

 

2. Unambiguous Grammar-

 

A grammar is said to unambiguous if for every string generated by it, it produces exactly one-

• Parse tree
• Or derivation tree
• Or syntax tree
• Or leftmost derivation
• Or rightmost derivation

 

Example-

 

Consider the following grammar-

E → E + T / T

T → T x F / F

F → id

Unambiguous Grammar

 

This grammar is an example of unambiguous grammar.

 

Also Read- Removing Ambiguity From Ambiguous Grammar

 

To gain better understanding about Ambiguous Grammar,

Watch this Video Lecture

 

Next Article- Recursive Grammar

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.