Advantages of Carry Look Ahead Adder over Ripple Carry Adder

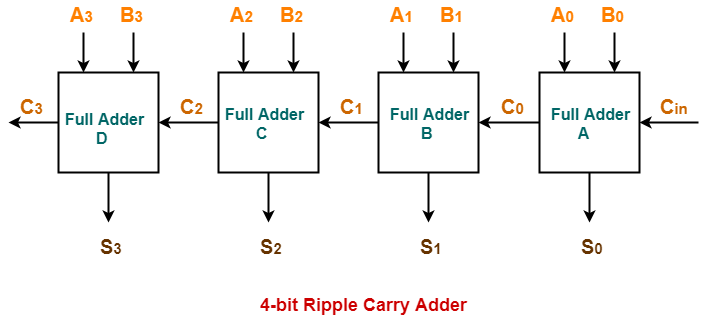
Ripple Carry Adder-

Before you go through this article, make sure that you have gone through the previous article on Ripple Carry Adder.

In Ripple Carry Adder,

Each full adder has to wait for its carry-in from its previous stage full adder.
Thus, n^th full adder has to wait until all (n-1) full adders have completed their operations.
This causes a delay and makes ripple carry adder extremely slow.
The situation becomes worst when the value of n becomes very large.
To overcome this disadvantage, Carry Look Ahead Adder comes into play.

In this article, we will discuss about Carry Look Ahead Adder.

Carry Look Ahead Adder-

Carry Look Ahead Adder is an improved version of the ripple carry adder.
It generates the carry-in of each full adder simultaneously without causing any delay.
The time complexity of carry look ahead adder = Θ (logn).

Logic Diagram-

The logic diagram for carry look ahead adder is as shown below-

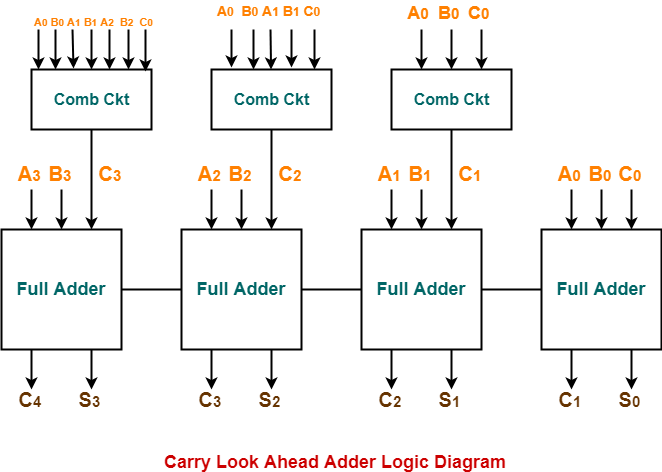
Carry Look Ahead Adder Working-

The working of carry look ahead adder is based on the principle-

The carry-in of any stage full adder is independent of the carry bits generated during intermediate stages.

The carry-in of any stage full adder depends only on the following two parameters-

Bits being added in the previous stages
Carry-in provided in the beginning

Now,

The above two parameters are always known from the beginning.
So, the carry-in of any stage full adder can be evaluated at any instant of time.
Thus, any full adder need not wait until its carry-in is generated by its previous stage full adder.

Also Read- Full Adder Working

4-Bit Carry Look Ahead Adder-

Consider two 4-bit binary numbers A₃A₂A₁A₀ and B₃B₂B₁B₀ are to be added.

Mathematically, the two numbers will be added as-

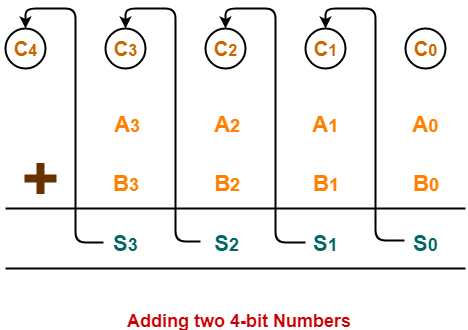
From here, we have-

C₁ = C₀ (A₀ ⊕ B₀) + A₀B₀

C₂ = C₁ (A₁ ⊕ B₁) + A₁B₁

C₃ = C₂ (A₂ ⊕ B₂) + A₂B₂

C₄ = C₃ (A₃ ⊕ B₃) + A₃B₃

For simplicity, Let-

G_i = A_iB_i where G is called carry generator
P_i = A_i ⊕ B_i where P is called carry propagator

Then, re-writing the above equations, we have-

C₁ = C₀P₀ + G₀………….. (1)

C₂ = C₁P₁ + G₁………….. (2)

C₃ = C₂P₂ + G₂………….. (3)

C₄ = C₃P₃ + G₃………….. (4)

Now,

Clearly, C1, C2 and C3 are intermediate carry bits.
So, let’s remove C₁, C₂ and C₃ from RHS of every equation.
Substituting (1) in (2), we get C₂ in terms of C₀.
Then, substituting (2) in (3), we get C₃ in terms of C₀ and so on.

Finally, we have the following equations-

C₁ = C₀P₀ + G₀
C₂ = C₀P₀P₁ + G₀P₁ + G₁
C₃ = C₀P₀P₁P₂ + G₀P₁P₂ + G₁P₂ + G₂
C₄ =C₀P₀P₁P₂P3 + G₀P₁P₂P₃ + G₁P₂P₃ + G₂P₃ + G₃

These equations are important to remember.

These equations show that the carry-in of any stage full adder depends only on-

Bits being added in the previous stages
Carry bit which was provided in the beginning

Trick To Memorize Above Equations-

As an example, let us consider the equation for generating carry bit C₂.

There are three possible reasons for generation of C₂ as depicted in the following picture-

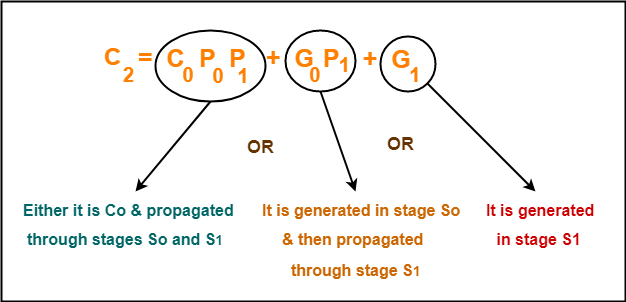
In the similar manner, we can write other equations as well very easily.

Implementation Of Carry Generator Circuits-

The above carry generator circuits are usually implemented as-

Two level combinational circuits.
Using AND and OR gates where gates are assumed to have any number of inputs.

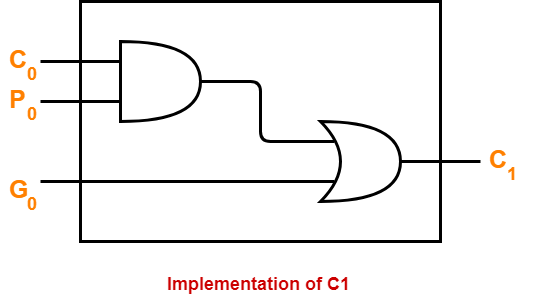
Implementation Of C₁–

The carry generator circuit for C1 is implemented as shown below.
It requires 1 AND gate and 1 OR gate.

C₁ = C₀P₀ + G₀

Implementation Of C₂–

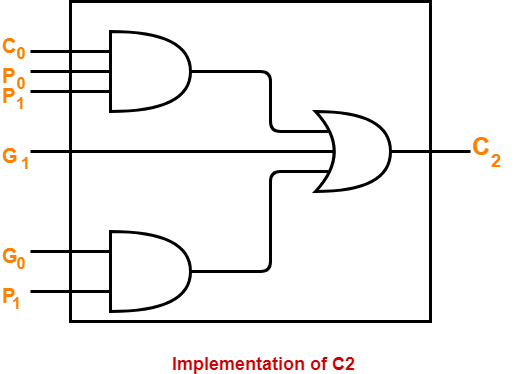
The carry generator circuit for C2 is implemented as shown below.
It requires 2 AND gates and 1 OR gate.

C₂ = C₀P₀P₁ + G₀P₁ + G₁

Implementation Of C₃ & C₄–

Similarly, we implement C₃ and C₄.

Implementation of C₃ uses 3 AND gates and 1 OR gate.
Implementation of C₄uses 4 AND gates and 1 OR gate.

Total number of gates required to implement carry generators (provided carry propagators P_i and carry generators G_i) are-

Total number of AND gates required for addition of 4-bit numbers = 1 + 2 + 3 + 4 = 10.
Total number of OR gates required for addition of 4-bit numbers = 1 + 1 + 1 + 1 = 4.

General Formula-

The following formula is used to calculate number of gates required for evaluating all carry bits-

For a n-bit carry look ahead adder to evaluate all the carry bits, it requires-

Number of AND gates = n(n+1) / 2
Number of OR gates = n