Sliding Window Protocol | Flow Control

Flow Control Protocols-

 

In computer networking, there are various flow control protocols-

 

 

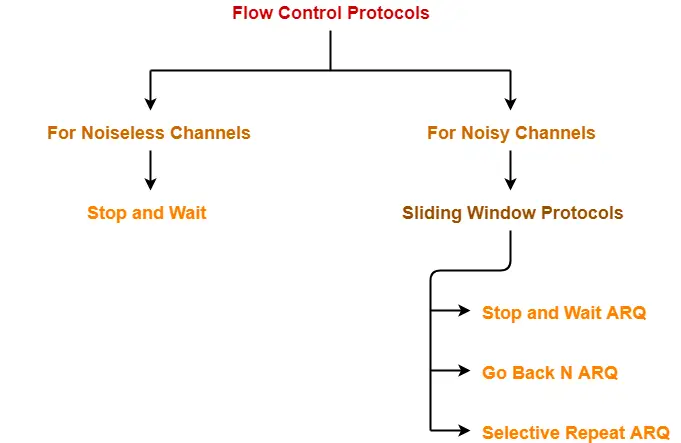
In this article, we will discuss about sliding window protocol.

 

Sliding Window Protocol-

 

• Sliding window protocol is a flow control protocol.
• It allows the sender to send multiple frames before needing the acknowledgements.
• Sender slides its window on receiving the acknowledgements for the sent frames.
• This allows the sender to send more frames.
• It is called so because it involves sliding of sender’s window.

 

Maximum number of frames that sender can send without acknowledgement = Sender window size

 

Optimal Window Size-

 

In a sliding window protocol, optimal sender window size = 1 + 2a

 

Derivation-

 

We know,

 

 

To get 100% efficiency, we must have-

η = 1

T_t / (T_t + 2T_p) = 1

T_t = T_t + 2T_p

 

Thus,

• To get 100% efficiency, transmission time must be T_t + 2T_p instead of T_t.
• This means sender must send the frames in waiting time too.
• Now, let us find the maximum number of frames that can be sent in time T_t + 2T_p.

 

We have-

• In time T_t, sender sends one frame.
• Thus, In time T_t + 2T_p, sender can send (T_t + 2T_p) / T_t frames i.e. 1+2a frames.

 

Thus, to achieve 100% efficiency, window size of the sender must be 1+2a.

 

Required Sequence Numbers-

 

• Each sending frame has to be given a unique sequence number.
• Maximum number of frames that can be sent in a window = 1+2a.
• So, minimum number of sequence numbers required = 1+2a.

 

To have 1+2a sequence numbers, Minimum number of bits required in sequence number field = ⌈log2(1+2a)⌉

 

NOTE-

 

• When minimum number of bits is asked, we take the ceil.
• When maximum number of bits is asked, we take the floor.

 

Choosing a Window Size-

 

The size of the sender’s window is bounded by-

 

1. Receiver’s Ability-

 

• Receiver’s ability to process the data bounds the sender window size.
• If receiver can not process the data fast, sender has to slow down and not transmit the frames too fast.

 

2. Sequence Number Field-

 

• Number of bits available in the sequence number field also bounds the sender window size.
• If sequence number field contains n bits, then 2ⁿ sequence numbers are possible.
• Thus, maximum number of frames that can be sent in one window = 2ⁿ.

 

For n bits in sequence number field, Sender Window Size = min (1+2a , 2n)

 

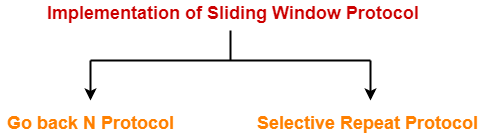
Implementations of Sliding Window Protocol-

 

The two well known implementations of sliding window protocol are-

 

 

1. Go back N Protocol
2. Selective Repeat Protocol

 

Efficiency-

 

Efficiency of any flow control protocol may be expressed as-

 

 

Example-

 

In Stop and Wait ARQ, sender window size = 1.

Thus,

Efficiency of Stop and Wait ARQ = 1 / 1+2a

 

PRACTICE PROBLEMS BASED ON SLIDING WINDOW PROTOCOL-

 

Problem-01:

 

If transmission delay and propagation delay in a sliding window protocol are 1 msec and 49.5 msec respectively, then-

1. What should be the sender window size to get the maximum efficiency?
2. What is the minimum number of bits required in the sequence number field?
3. If only 6 bits are reserved for sequence numbers, then what will be the efficiency?

 

Solution-

 

Given-

• Transmission delay = 1 msec
• Propagation delay = 49.5 msec

 

Part-01:

 

To get the maximum efficiency, sender window size

= 1 + 2a

= 1 + 2 x (T_p / T_t)

= 1 + 2 x (49.5 msec / 1 msec)

= 1 + 2 x 49.5

= 100

Thus,

For maximum efficiency, sender window size = 100

 

Part-02:

 

Minimum number of bits required in the sequence number field

= ⌈log₂(1+2a)⌉

= ⌈log₂(100)⌉

= ⌈6.8⌉

= 7

Thus,

Minimum number of bits required in the sequence number field = 7

 

Part-03:

 

If only 6 bits are reserved in the sequence number field, then-

Maximum sequence numbers possible = 2⁶ = 64

Now,

Efficiency

= Sender window size in the protocol / Optimal sender window size

= 64 / 100

= 0.64

= 64%

 

Problem-02:

 

If transmission delay and propagation delay in a sliding window protocol are 1 msec and 99.5 msec respectively, then-

1. What should be the sender window size to get the maximum efficiency?
2. What is the minimum number of bits required in the sequence number field?
3. If only 7 bits are reserved for sequence numbers, then what will be the efficiency?

 

Solution-

 

Given-

• Transmission delay = 1 msec
• Propagation delay = 99.5 msec

 

Part-01:

 

To get the maximum efficiency, sender window size

= 1 + 2a

= 1 + 2 x (T_p / T_t)

= 1 + 2 x (99.5 msec / 1 msec)

= 1 + 2 x 99.5

= 200

Thus,

For maximum efficiency, sender window size = 200

 

Part-02:

 

Minimum number of bits required in the sequence number field

= ⌈log₂(1+2a)⌉

= ⌈log₂(200)⌉

= ⌈7.64⌉

= 8

Thus,

Minimum number of bits required in the sequence number field = 8

 

Part-03:

 

If only 6 bits are reserved in the sequence number field, then-

Maximum sequence numbers possible = 2⁷ = 128

Now,

Efficiency

= Sender window size in the protocol / Optimal sender window size

= 128 / 200

= 0.64

= 64%

 

To gain better understanding about sliding window protocol,

Watch this Video Lecture

 

Next Article- Practice Problems On Sliding Window Protocol

 

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.