Set Theory Operators | Relational Algebra | DBMS

Relational Algebra Operators-

 

Before you go through this article, make sure that you have gone through the previous article on Introduction to Relational Algebra.

 

The operators in relational algebra are classified as-

 

 

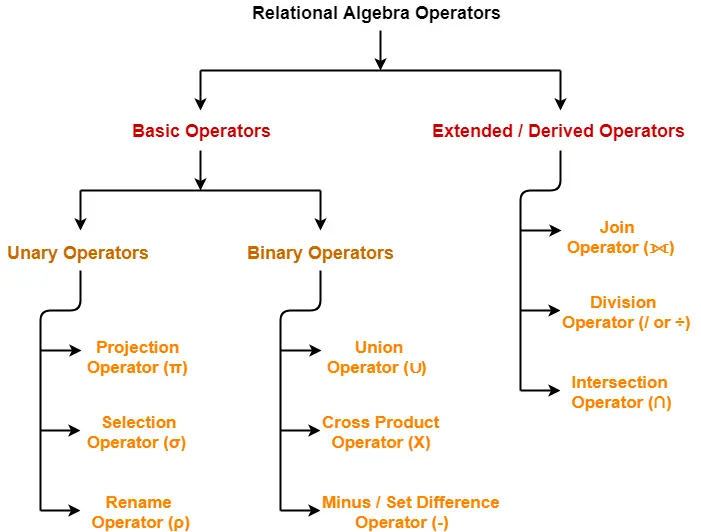
In this article, we will discuss about Set Theory Operators.

 

Set Theory Operators-

 

Following operators are called as set theory operators-

 

 

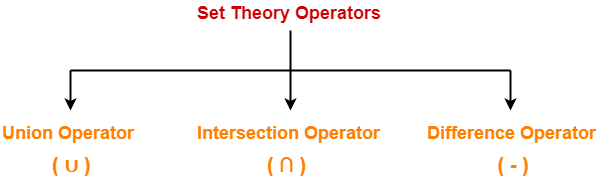
1. Union Operator (∪)
2. Intersection Operator (∩)
3. Difference Operator (-)

 

Condition For Using Set Theory Operators   To use set theory operators on two relations, The two relations must be union compatible. Union compatible property means- Both the relations must have same number of attributes. The attribute domains (types of values accepted by attributes) of both the relations must be compatible.

 

Also read- Selection Operator and Projection Operator

 

1. Union Operator (∪)-

 

Let R and S be two relations.

Then-

• R ∪ S is the set of all tuples belonging to either R or S or both.
• In R ∪ S, duplicates are automatically removed.
• Union operation is both commutative and associative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R ∪ S is-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science
400	Kajol	French

Relation R ∪ S

 

2. Intersection Operator (∩)-

 

Let R and S be two relations.

Then-

• R ∩ S is the set of all tuples belonging to both R and S.
• In R ∩ S, duplicates are automatically removed.
• Intersection operation is both commutative and associative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R ∩ S is-

 

ID	Name	Subject
100	Ankit	English

Relation R ∩ S

 

3. Difference Operator (-)-

 

Let R and S be two relations.

Then-

• R – S is the set of all tuples belonging to R and not to S.
• In R – S, duplicates are automatically removed.
• Difference operation is associative but not commutative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R – S is-

 

ID	Name	Subject
200	Pooja	Maths
300	Komal	Science

Relation R – S

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.