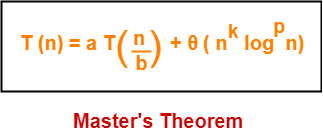Master Theorem | Master Theorem Examples

Master Theorem-

 

Master’s Theorem is a popular method for solving the recurrence relations.

 

Master’s theorem solves recurrence relations of the form-

 

 

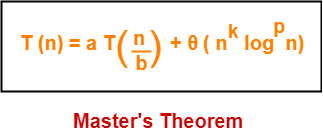
Here, a >= 1, b > 1, k >= 0 and p is a real number.

 

Master Theorem Cases-

 

To solve recurrence relations using Master’s theorem, we compare a with b^k.

Then, we follow the following cases-

 

Case-01:

 

If a > b^k, then T(n) = θ (n^log_ba)

 

Case-02:

 

If a = b^k and

• If p < -1, then T(n) = θ (n^log_ba)
• If p = -1, then T(n) = θ (n^log_ba.log²n)
• If p > -1, then T(n) = θ (n^log_ba.log^p+1n)

 

Case-03:

 

If a < b^k and

• If p < 0,  then T(n) = O (n^k)
• If p >= 0, then T(n) = θ (n^klog^pn)

 

PRACTICE PROBLEMS BASED ON MASTER THEOREM-

 

Problem-01:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = 3T(n/2) + n²

 

Solution-

 

We compare the given recurrence relation with T(n) = aT(n/b) + θ (n^klog^pn).

Then, we have-

a = 3

b = 2

k = 2

p = 0

 

Now, a = 3 and b^k = 2² = 4.

Clearly, a < b^k.

So, we follow case-03.

 

Since p = 0, so we have-

T(n) = θ (n^klog^pn)

T(n) = θ (n²log⁰n)

 

Thus,

T(n) = θ (n2)

 

Problem-02:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = 2T(n/2) + nlogn

 

Solution-

 

We compare the given recurrence relation with T(n) = aT(n/b) + θ (n^klog^pn).

Then, we have-

a = 2

b = 2

k = 1

p = 1

 

Now, a = 2 and b^k = 2¹ = 2.

Clearly, a = b^k.

So, we follow case-02.

 

Since p = 1, so we have-

T(n) = θ (n^log_ba.log^p+1n)

T(n) = θ (n^log₂2.log¹⁺¹n)

 

Thus,

T(n) = θ (nlog2n)

 

Problem-03:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = 2T(n/4) + n^0.51

 

Solution-

 

We compare the given recurrence relation with T(n) = aT(n/b) + θ (n^klog^pn).

Then, we have-

a = 2

b = 4

k = 0.51

p = 0

 

Now, a = 2 and b^k = 4^0.51 = 2.0279.

Clearly, a < b^k.

So, we follow case-03.

 

Since p = 0, so we have-

T(n) = θ (n^klog^pn)

T(n) = θ (n^0.51log⁰n)

 

Thus,

T(n) = θ (n0.51)

 

Problem-04:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = √2T(n/2) + logn

 

Solution-

 

We compare the given recurrence relation with T(n) = aT(n/b) + θ (n^klog^pn).

Then, we have-

a = √2

b = 2

k = 0

p = 1

 

Now, a = √2 = 1.414 and b^k = 2⁰ = 1.

Clearly, a > b^k.

So, we follow case-01.

 

So, we have-

T(n) = θ (n^log_ba)

T(n) = θ (n^log₂√2)

T(n) = θ (n^1/2)

 

Thus,

T(n) = θ (√n)

 

Problem-05:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = 8T(n/4) – n²logn

 

Solution-

 

• The given recurrence relation does not correspond to the general form of Master’s theorem.
• So, it can not be solved using Master’s theorem.

 

Problem-06:

 

Solve the following recurrence relation using Master’s theorem-

T(n) = 3T(n/3) + n/2

 

Solution-

 

• We write the given recurrence relation as T(n) = 3T(n/3) + n.
• This is because in the general form, we have θ for function f(n) which hides constants in it.
• Now, we can easily apply Master’s theorem.

 

We compare the given recurrence relation with T(n) = aT(n/b) + θ (n^klog^pn).

Then, we have-

a = 3

b = 3

k = 1

p = 0

 

Now, a = 3 and b^k = 3¹ = 3.

Clearly, a = b^k.

So, we follow case-02.

 

Since p = 0, so we have-

T(n) = θ (n^log_ba.log^p+1n)

T(n) = θ (n^log₃3.log⁰⁺¹n)

T(n) = θ (n¹.log¹n)

 

Thus,

T(n) = θ (nlogn)

 

Problem-07:

 

Form a recurrence relation for the following code and solve it using Master’s theorem-

 

A(n)
{
   if(n<=1)
     return 1;
   else
     return A(√n);
}

 

Solution-

 

• We write a recurrence relation for the given code as T(n) = T(√n) + 1.
• Here 1 = Constant time taken for comparing and returning the value.
• We can not directly apply Master’s Theorem on this recurrence relation.
• This is because it does not correspond to the general form of Master’s theorem.
• However, we can modify and bring it in the general form to apply Master’s theorem.

 

Let-

n = 2^m    ……(1)

Then-

T(2^m) = T(2^m/2) + 1

 

Now, let T(2^m) = S(m), then T(2^m/2) = S(m/2)

 

So, we have-

S(m) = S(m/2) +1

Now, we can easily apply Master’s Theorem.

 

We compare the given recurrence relation with S(m) = aS(m/b) + θ (m^klog^pm).

Then, we have-

a = 1

b = 2

k = 0

p = 0

 

Now, a = 1 and b^k = 2⁰ = 1.

Clearly, a = b^k.

So, we follow case-02.

 

Since p = 0, so we have-

S(m) = θ (m^log_ba.log^p+1m)

S(m) = θ (m^log₂1.log⁰⁺¹m)

S(m) = θ (m⁰.log¹m)

 

Thus,

S(m) = θ(logm)    ……(2)

 

Now,

• From (1), we have n = 2^m.
• So, logn = mlog2 which implies m = log₂n.

 

Substituting in (2), we get-

S(m) = θ(loglog₂n)

Or

T(n) = θ (loglog2n)

 

To gain better understanding about Master’s Theorem,

Watch this Video Lecture

 

Next Article- Recursion Tree

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.