Propositions-
Before you go through this article, make sure that you have gone through the previous article on Propositions.
We have discussed-
- Proposition is a declarative statement that is either true or false but not both.
- Connectives are used to combine the propositions.

In this article, we will discuss about connectives in propositional logic.
Logical Connectives-
| Connectives are the operators that are used to combine one or more propositions. |
In propositional logic, there are 5 basic connectives-

| Name of Connective | Connective Word | Symbol |
| Negation | Not | ⌉ or ∼ or ‘ or – |
| Conjunction | And | ∧ |
| Disjunction | Or | ∨ |
| Conditional | If-then | → |
| Biconditional | If and only if | ↔ |
1. Negation-
If p is a proposition, then negation of p is a proposition which is-
- True when p is false
- False when p is true.
Truth Table-
| p | ∼p |
| F | T |
| T | F |
Example-
If p : It is raining outside.
Then, Negation of p is-
∼p : It is not raining outside.
2. Conjunction-
If p and q are two propositions, then conjunction of p and q is a proposition which is-
- True when both p and q are true
- False when both p and q are false
Truth Table-
| p | q | p ∧ q |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
Example-
If p and q are two propositions where-
- p : 2 + 4 = 6
- q : It is raining outside.
Then, conjunction of p and q is-
p ∧ q : 2 + 4 = 6 and it is raining outside
3. Disjunction-
If p and q are two propositions, then disjunction of p and q is a proposition which is-
- True when either one of p or q or both are true
- False when both p and q are false
Truth Table-
| p | q | p ∨ q |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
Example-
If p and q are two propositions where-
- p : 2 + 4 = 6
- q : It is raining outside
Then, disjunction of p and q is-
p ∨ q : 2 + 4 = 6 or it is raining outside
4. Conditional-
If p and q are two propositions, then-
- Proposition of the type “If p then q” is called a conditional or implication proposition.
- It is true when both p and q are true or when p is false.
- It is false when p is true and q is false.
Truth Table-
| p | q | p → q |
| F | F | T |
| F | T | T |
| T | F | F |
| T | T | T |
Examples-
- If a = b and b = c then a = c.
- If I will go to Australia, then I will earn more money.
5. Biconditional-
If p and q are two propositions, then-
- Proposition of the type “p if and only if q” is called a biconditional or bi-implication proposition.
- It is true when either both p and q are true or both p and q are false.
- It is false in all other cases.
Truth Table-
| p | q | p ↔ q |
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
Examples-
- He goes to play a match if and only if it does not rain.
- Birds fly if and only if sky is clear.
Important Notes-
Note-01:
- Negation ≡ NOT Gate of digital electronics.
- Conjunction ≡ AND Gate of digital electronics.
- Disjunction ≡ OR Gate of digital electronics.
- Biconditional = EX-NOR Gate of digital electronics.
Note-02:
- Each logical connective has some priority.
- This priority order is important while solving questions.
- The decreasing order of priority is-
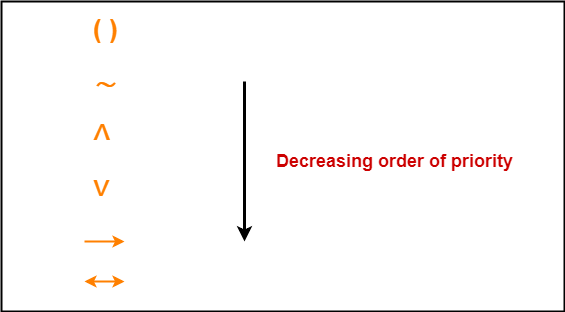
Note-03:
- Negation, Conjunction, Disjunction and Biconditional are both commutative and associative.
- Conditional is neither commutative nor associative.
To gain better understanding about Logical Connectives,
Next Article- Converting English Sentences To Propositional Logic
Get more notes and other study material of Propositional Logic.

