Relationship Between Left Recursion, Left Factoring & Ambiguity-
| There is no relationship between Left Recursion, Left Factoring and Ambiguity of Grammar. |
- All the three concepts are independent and has nothing to do with each other.
- The presence or absence of left recursion does not impact left factoring and ambiguity anyhow.
- The presence or absence of left factoring does not impact left recursion and ambiguity anyhow.
- The presence or absence of ambiguity does not impact left recursion and left factoring anyhow.
The following examples support this fact-
Example-01: Ambiguous Grammar With Left Factoring-
Consider the following grammar-
S → aS / a / ∈
Clearly, this grammar has left factoring.
Now, let us draw parse trees for the string w = a-
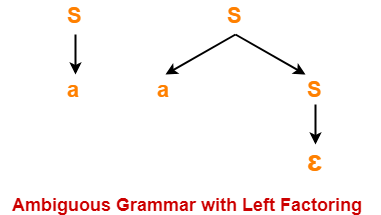
Clearly,
- Two different parse trees exist for the string w = a.
- Therefore, the grammar is ambiguous.
Example-02: Unambiguous Grammar With Left Factoring-
Consider the following grammar-
S → aA / aB
A → a
B → b
Clearly, this grammar has left factoring.
The language generated by this grammar consists of only two strings L(G) = { aa , ab}.
Now, let us draw parse trees for these strings-
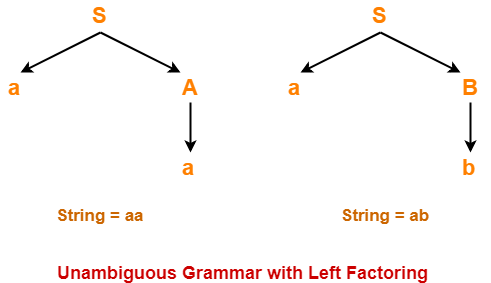
Clearly,
- A unique parse tree exists for both the strings.
- Therefore, the grammar is unambiguous.
Example-03: Ambiguous Grammar With Left Recursion-
Consider the following grammar-
S → SS / ∈
Clearly, this grammar has left recursion.
Now, let us draw parse trees for the string w = ∈-
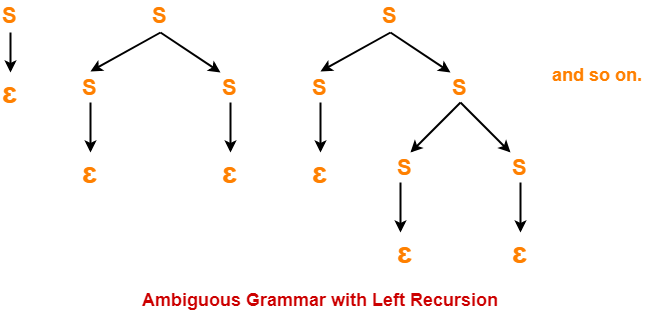
Clearly,
- Infinite parse trees exist for the string w = ∈.
- Therefore, the grammar is ambiguous.
Example-04: Unambiguous Grammar With Left Recursion-
Consider the following grammar-
S → Sa / ∈
Clearly, this grammar has left recursion.
A unique parse tree exists for all the strings that can be generated from the grammar.
Therefore, the grammar is unambiguous.
Example-05: Ambiguous Grammar Without Left Recursion & Without Left Factoring-
Consider the following grammar-
S → aA / Ba
A → a
B → a
Clearly, this grammar has neither left recursion nor left factoring.
Now, let us draw parse trees for the string w = aa-
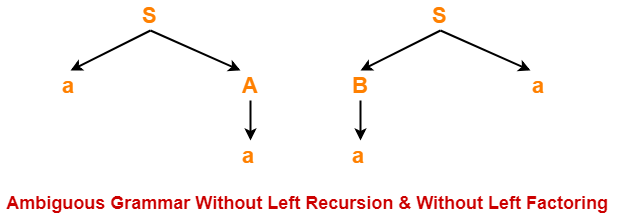
Clearly,
- Two different parse trees exist for the string w = aa.
- Therefore, the grammar is ambiguous.
Example-06: Unambiguous Grammar With Both Left Recursion & Left Factoring-
Consider the following grammar-
S → Sa / ɛ / bB / bD
B → b
D → d
Clearly, this grammar has both left recursion and left factoring.
A unique parse tree exists for all the strings that can be generated from the grammar.
Therefore, the grammar is unambiguous.
To gain better understanding about relationship between left recursion, left factoring and ambiguity-
Download Handwritten Notes Here-
Next Article- Calculating First and Follow
Get more notes and other study material of Compiler Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.


