Language Of Grammar-
| Language of Grammar is the set of all strings that can be generated from that grammar. |
- If the language consists of finite number of strings, then it is called as a Finite language.
- If the language consists of infinite number of strings, then it is called as an Infinite language.
Also Read- Grammar in Automata
Example-01:
Consider a grammar G = (V , T , P , S) where-
- V = { S }
- T = { a , b }
- P = { S → aSbS , S → bSaS , S → ∈ }
- S = { S }
This grammar generates the strings having equal number of a’s and b’s.
So, Language of this grammar is-
| L(G) = { ∈ , ab , ba , aabb , bbaa , abab , baba , …… } |
- This language consists of infinite number of strings.
- Therefore, language of the grammar is infinite.
Example-02:
Consider a grammar G = (V , T , P , S) where-
- V = { S , A , B , C }
- T = { a , b , c }
- P = { S → ABC , A → a , B → b , C → c }
- S = { S }
This grammar generates only one string “abc”.
So, Language of this grammar is-
| L(G) = { abc } |
- This language consists of finite number of strings.
- Therefore, language of the grammar is finite.
Also Read- Deciding Language Is Finite Or Infinite
Important Concept-
- For any given grammar, the language generated by it is always unique.
- For any given language, we may have more than one grammar generating that language.
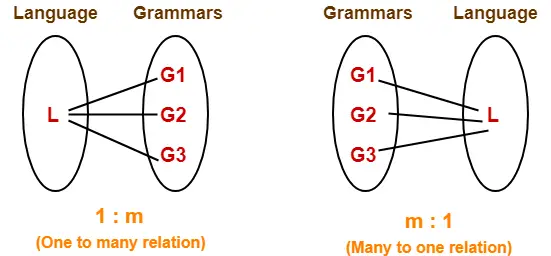
Example-
Consider the following two grammars-
Grammar G1-
S → AB
A → a
B → b
The language generated by this grammar is-
L(G1) = { ab }
Grammar G2-
S → AB
A → ∈
B → ab
The language generated by this grammar is-
L(G2) = { ab }
Here,
- Both the grammars generate a unique language.
- But given a language L(G) = { ab }, we have two different grammars generating that language.
This justifies the above concept.
Next Article- Language Ambiguity
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.

