Construction of DFA | DFA Solved Examples

Construction Of DFA-

 

In this article, we will learn the construction of DFA.

 

Type-01 Problems-

 

In Type-01 problems, we will discuss the construction of DFA for languages consisting of strings ending with a particular substring.

 

Steps To Construct DFA-

 

Following steps are followed to construct a DFA for Type-01 problems-

 

Step-01:

 

• Determine the minimum number of states required in the DFA.
• Draw those states.

 

Use the following rule to determine the minimum number of states-

 

RULE Calculate the length of substring. All strings ending with ‘n’ length substring will always require minimum (n+1) states in the DFA.

 

Step-02:

 

• Decide the strings for which DFA will be constructed.
• The method for deciding the strings has been discussed in this Video.

 

Step-03:

 

• Construct a DFA for the strings decided in Step-02.

 

Remember the following rule while constructing the DFA-

 

RULE While constructing a DFA, Always prefer to use the existing path. Create a new path only when there exists no path to go with.

 

Step-04:

 

• Send all the left possible combinations to the starting state.
• Do not send the left possible combinations over the dead state.

 

PRACTICE PROBLEMS BASED ON CONSTRUCTION OF DFA-

 

Problem-01:

 

Draw a DFA for the language accepting strings ending with ’01’ over input alphabets ∑ = {0, 1}

 

Solution-

 

Regular expression for the given language = (0 + 1)*01

 

Step-01:

 

• All strings of the language ends with substring “01”.
• So, length of substring = 2.

 

Thus, Minimum number of states required in the DFA = 2 + 1 = 3.

It suggests that minimized DFA will have 3 states.

 

Step-02:

 

We will construct DFA for the following strings-

• 01
• 001
• 0101

 

Step-03:

 

The required DFA is-

 

 

Problem-02:

 

Draw a DFA for the language accepting strings ending with ‘abb’ over input alphabets ∑ = {a, b}

 

Solution-

 

Regular expression for the given language = (a + b)*abb

 

Step-01:

 

• All strings of the language ends with substring “abb”.
• So, length of substring = 3.

 

Thus, Minimum number of states required in the DFA = 3 + 1 = 4.

It suggests that minimized DFA will have 4 states.

 

Step-02:

 

We will construct DFA for the following strings-

• abb
• aabb
• ababb
• abbabb

 

Step-03:

 

The required DFA is-

 

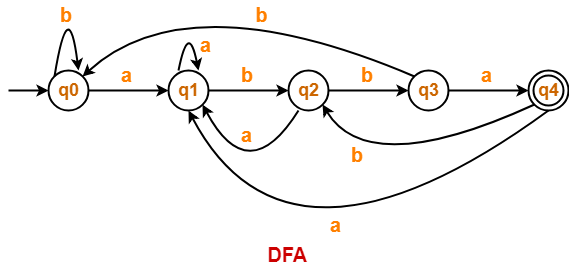
Problem-03:

 

Draw a DFA for the language accepting strings ending with ‘abba’ over input alphabets ∑ = {a, b}

 

Solution-

 

Regular expression for the given language = (a + b)*abba

 

Step-01:

 

• All strings of the language ends with substring “abba”.
• So, length of substring = 4.

 

Thus, Minimum number of states required in the DFA = 4 + 1 = 5.

It suggests that minimized DFA will have 5 states.

 

Step-02:

 

We will construct DFA for the following strings-

• abba
• aabba
• ababba
• abbabba
• abbaabba

 

Step-03:

 

The required DFA is-

 

 

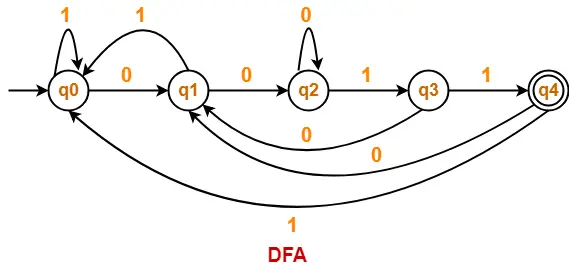
Problem-04:

 

Draw a DFA for the language accepting strings ending with ‘0011’ over input alphabets ∑ = {0, 1}

 

Solution-

 

Regular expression for the given language = (0 + 1)*0011

 

Step-01:

 

• All strings of the language ends with substring “0011”.
• So, length of substring = 4.

 

Thus, Minimum number of states required in the DFA = 4 + 1 = 5.

It suggests that minimized DFA will have 5 states.

 

Step-02:

 

We will construct DFA for the following strings-

• 0011
• 00011
• 000011
• 0010011
• 00110011

 

Step-03:

 

The required DFA is-

 

 

Also Read- Converting DFA to Regular Expression

 

To gain better understanding about Construction of DFA,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Construction of DFA | Type-02 Problems

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.