Heap Data Structure-
Before you go through this article, make sure that you have gone through the previous article on Heap Data Structure.
We have discussed-
- Heap is a specialized data structure with special properties.
- A binary heap is a binary tree that has ordering and structural properties.
- A heap may be a max heap or a min heap.
In this article, we will discuss about heap operations.
Heap Operations-
The most basic and commonly performed operations on a heap are-

- Search Operation
- Insertion Operation
- Deletion Operation
Here, we will discuss how these operations are performed on a max heap.
Max Heap-
- In max heap, every node contains greater or equal value element than its child nodes.
- Thus, root node contains the largest value element.
Example-
The following heap is an example of a max heap-
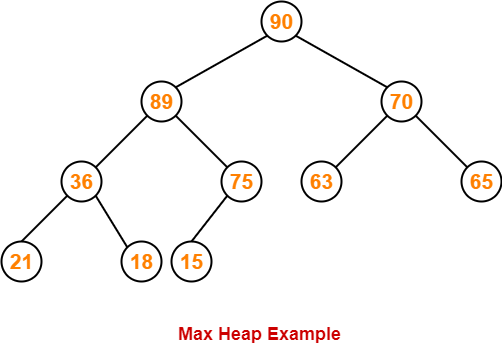
Max Heap Operations-
We will discuss the construction of a max heap and how following operations are performed on a max heap-
- Finding Maximum Operation
- Insertion Operation
- Deletion Operation
Max Heap Construction-
Given an array of elements, the steps involved in constructing a max heap are-
Step-01:
Convert the given array of elements into an almost complete binary tree.
Step-02:
Ensure that the tree is a max heap.
- Check that every non-leaf node contains a greater or equal value element than its child nodes.
- If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
- Start checking from a non-leaf node with the highest index (bottom to top and right to left).
Finding Maximum Operation-
- In max heap, the root node always contains the maximum value element.
- So, we directly display the root node value as maximum value in max heap.
Insertion Operation-
| Insertion Operation is performed to insert an element in the heap tree. |
The steps involved in inserting an element are-
Step-01:
Insert the new element as a next leaf node from left to right.
Step-02:
Ensure that the tree remains a max heap.
- Check that every non-leaf node contains a greater or equal value element than its child nodes.
- If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
- Start checking from a non-leaf node with the highest index (bottom to top and right to left).
Deletion Operation-
| Deletion Operation is performed to delete a particular element from the heap tree. |
When it comes to deleting a node from the heap tree, following two cases are possible-
Case-01: Deletion Of Last Node-
- This case is pretty simple.
- Just remove / disconnect the last leaf node from the heap tree.
Case-02: Deletion Of Some Other Node-
- This case is little bit difficult.
- Deleting a node other than the last node disturbs the heap properties.
The steps involved in deleting such a node are-
Step-01:
- Delete the desired element from the heap tree.
- Pluck the last node and put in place of the deleted node.
Step-02:
Ensure that the tree remains a max heap.
- Check that every non-leaf node contains a greater or equal value element than its child nodes.
- If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
- Start checking from a non-leaf node with the highest index (bottom to top and right to left).
PRACTICE PROBLEMS BASED ON MAX HEAP OPERATIONS-
Problem-01:
Construct a max heap for the given array of elements-
1, 5, 6, 8, 12, 14, 16
Solution-
Step-01:
We convert the given array of elements into an almost complete binary tree-
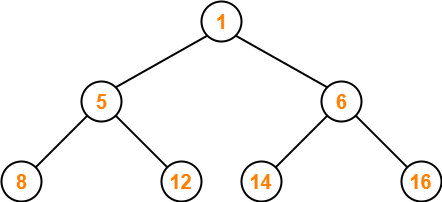
Step-02:
- We ensure that the tree is a max heap.
- Node 6 contains greater element in its right child node.
- So, we swap node 6 and node 16.
The resulting tree is-
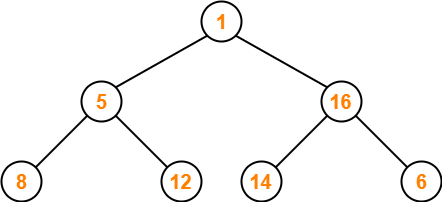
Step-03:
- Node 5 contains greater element in its right child node.
- So, we swap node 5 and node 12.
The resulting tree is-
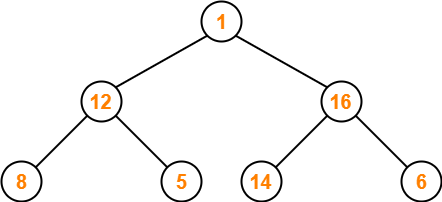
Step-04:
- Node 1 contains greater element in its right child node.
- So, we swap node 1 and node 16.
The resulting tree is-
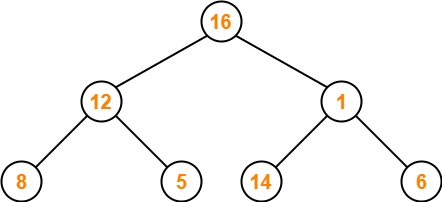
Step-05:
- Node 1 contains greater element in its left child node.
- So, we swap node 1 and node 14.
The resulting tree is-
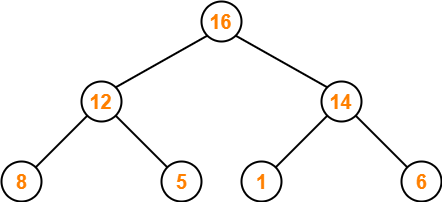
This is the required max heap for the given array of elements.
Problem-02:
Consider the following max heap-
50, 30, 20, 15, 10, 8, 16
Insert a new node with value 60.
Solution-
Step-01:
We convert the given array of elements into a heap tree-
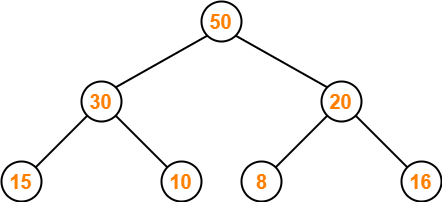
Step-02:
We insert the new element 60 as a next leaf node from left to right.
The resulting tree is-
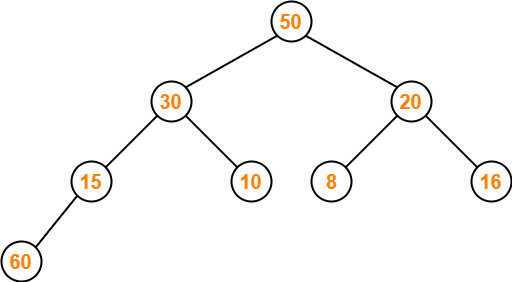
Step-03:
- We ensure that the tree is a max heap.
- Node 15 contains greater element in its left child node.
- So, we swap node 15 and node 60.
The resulting tree is-
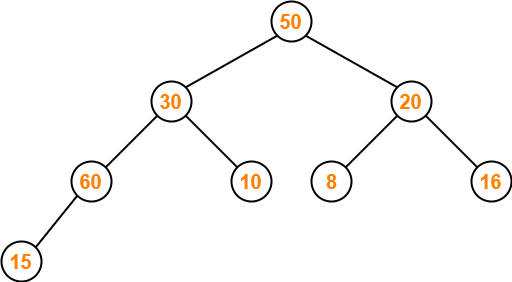
Step-04:
- Node 30 contains greater element in its left child node.
- So, we swap node 30 and node 60.
The resulting tree is-
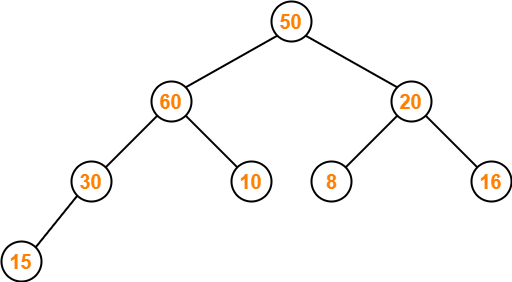
Step-05:
- Node 50 contains greater element in its left child node.
- So, we swap node 50 and node 60.
The resulting tree is-
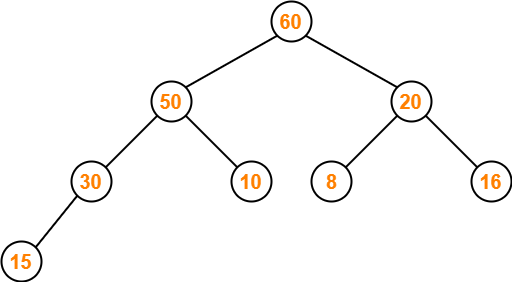
This is the required max heap after inserting the node with value 60.
Problem-03:
Consider the following max heap-
50, 30, 20, 15, 10, 8, 16
Delete a node with value 50.
Solution-
Step-01:
We convert the given array of elements into a heap tree-
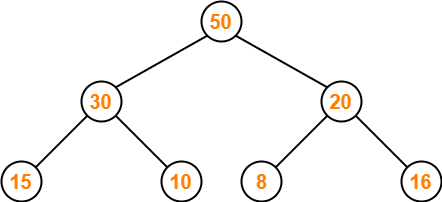
Step-02:
- We delete the element 50 which is present at root node.
- We pluck the last node 16 and put in place of the deleted node.
The resulting tree is-
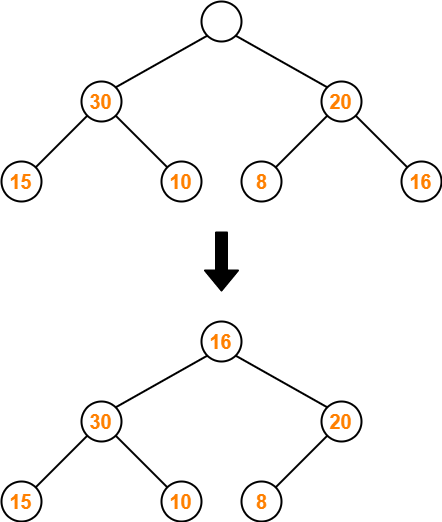
Step-03:
- We ensure that the tree is a max heap.
- Node 16 contains greater element in its left child node.
- So, we swap node 16 and node 30.
The resulting tree is-
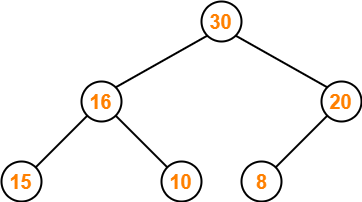
This is the required max heap after deleting the node with value 50.
To gain better understanding about Heap Data Structure,
Next Article- Introduction to Hashing
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.

