Grammar Ambiguity-
Before you go through this article, make sure that you have gone through the previous article on Ambiguous Grammar.
- There exists no algorithm to check whether any given grammar is ambiguous or not.
- This general decision problem is undecidable-
“Whether a grammar is ambiguous or not?”
- This is because it can be shown that this problem is equivalent to Post Correspondence Problem.
General Approach To Check Grammar Ambiguity-
To check whether a given grammar is ambiguous or not, we follow the following steps-
Step-01:
We try finding a string from the Language of Grammar such that for the string there exists more than one-
- parse tree
- or derivation tree
- or syntax tree
- or leftmost derivation
- or rightmost derivation
Step-02:
If there exists at least one such string, then the grammar is ambiguous otherwise unambiguous.
PROBLEMS BASED ON CHECKING WHETHER GRAMMAR IS AMBIGUOUS-
Problem-01:
Check whether the given grammar is ambiguous or not-
S → SS
S → a
S → b
Solution-
Let us consider a string w generated by the given grammar-
w = abba
Now, let us draw parse trees for this string w.
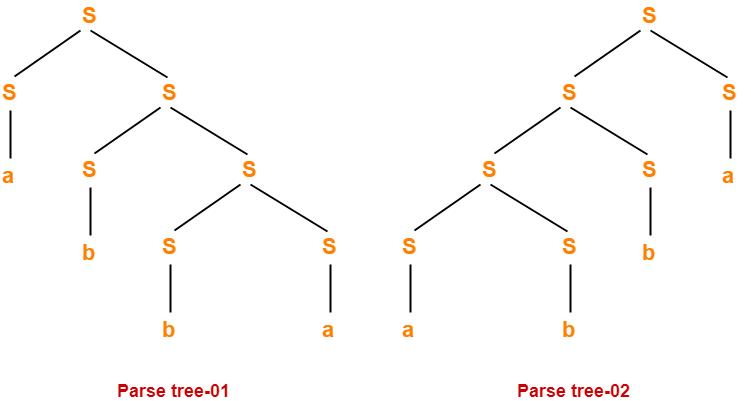
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-02:
Check whether the given grammar is ambiguous or not-
S → A / B
A → aAb / ab
B → abB / ∈
Solution-
Let us consider a string w generated by the given grammar-
w = ab
Now, let us draw parse trees for this string w.
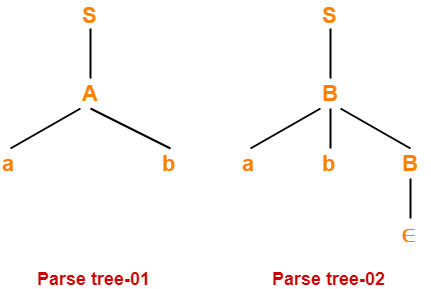
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-03:
Check whether the given grammar is ambiguous or not-
S → AB / C
A → aAb / ab
B → cBd / cd
C → aCd / aDd
D → bDc / bc
Solution-
Let us consider a string w generated by the given grammar-
w = aabbccdd
Now, let us draw parse trees for this string w.
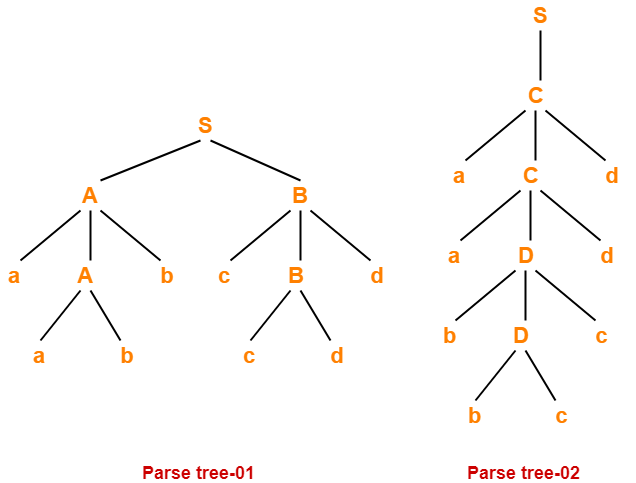
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-04:
Check whether the given grammar is ambiguous or not-
S → AB / aaB
A → a / Aa
B → b
Solution-
Let us consider a string w generated by the given grammar-
w = aab
Now, let us draw parse trees for this string w.
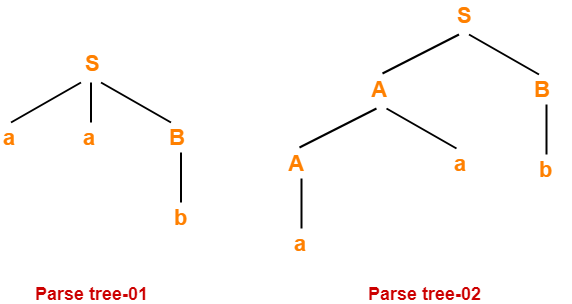
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-05:
Check whether the given grammar is ambiguous or not-
S → a / abSb / aAb
A → bS / aAAb
Solution-
Let us consider a string w generated by the given grammar-
w = abababb
Now, let us draw parse trees for this string w.
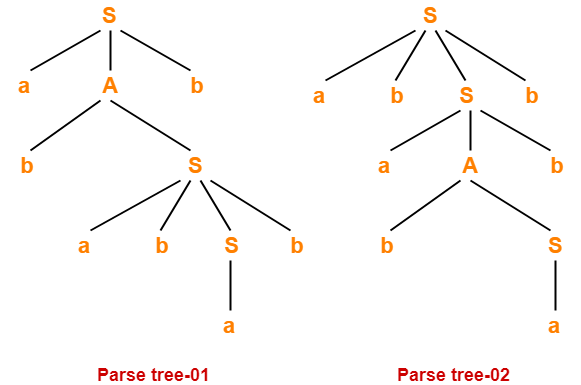
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-06:
Check whether the given grammar is ambiguous or not-
E → E + T / T
T → T x F / F
F → id
Solution-
- There exists no string belonging to the language of grammar which has more than one parse tree.
- Since a unique parse tree exists for all the strings, therefore the given grammar is unambiguous.
Problem-07:
Check whether the given grammar is ambiguous or not-
S → aSbS / bSaS / ∈
Solution-
Let us consider a string w generated by the given grammar-
w = abab
Now, let us draw parse trees for this string w.
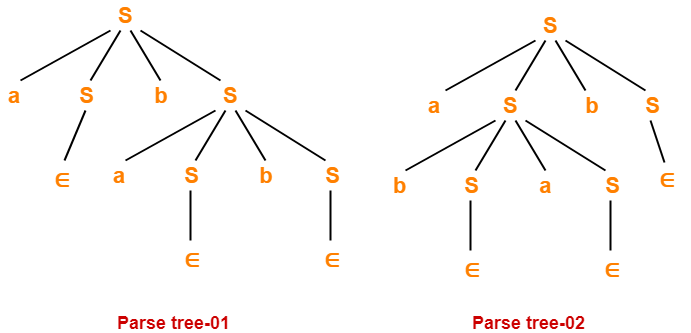
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
Problem-08:
Check whether the given grammar is ambiguous or not-
R → R + R / R . R / R* / a / b
Solution-
Let us consider a string w generated by the given grammar-
w = ab + a
Now, let us draw parse trees for this string w.
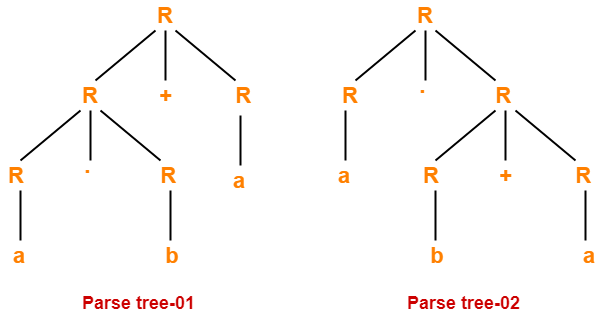
Since two different parse trees exist for string w, therefore the given grammar is ambiguous.
To gain better understanding about Grammar Ambiguity,
Next Article- Converting Ambiguous into Unambiguous Grammar
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.

