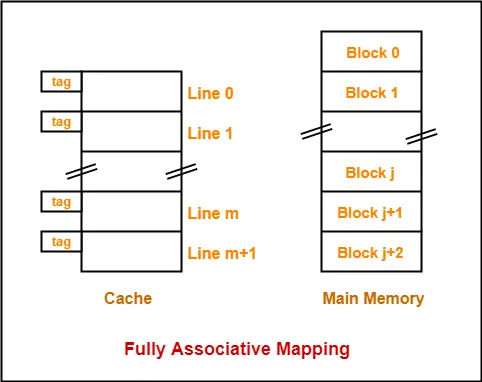
Fully Associative Mapping | Practice Problems

Fully Associative Mapping-

 

Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.

 

In fully associative mapping,

• A block of main memory can be mapped to any freely available cache line.
• This makes fully associative mapping more flexible than direct mapping.
• A replacement algorithm is needed to replace a block if the cache is full.

 

In this article, we will discuss practice problems based on fully associative mapping.

 

Also Read- Practice Problems On Direct Mapping

 

PRACTICE PROBLEMS BASED ON FULLY ASSOCIATIVE MAPPING-

 

Problem-01:

 

Consider a fully associative mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

1. Number of bits in tag
2. Tag directory size

 

Solution-

 

Given-

• Cache memory size = 16 KB
• Block size = Frame size = Line size = 256 bytes
• Main memory size = 128 KB

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

Thus, Number of bits in physical address = 17 bits

 

 

Number of Bits in Block Offset-

 

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

 

 

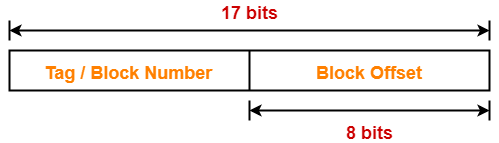
Number of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 17 bits – 8 bits

= 9 bits

Thus, Number of bits in tag = 9 bits

 

 

Number of Lines in Cache-

 

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 2⁶ lines

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁶ x 9 bits

= 576 bits

= 72 bytes

Thus, size of tag directory = 72 bytes

 

Problem-02:

 

Consider a fully associative mapped cache of size 512 KB with block size 1 KB. There are 17 bits in the tag. Find-

1. Size of main memory
2. Tag directory size

 

Solution-

 

Given-

• Cache memory size = 512 KB
• Block size = Frame size = Line size = 1 KB
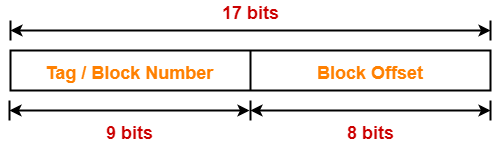
• Number of bits in tag = 17 bits

 

We consider that the memory is byte addressable.

 

Number of Bits in Block Offset-

 

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

 

 

Number of Bits in Physical Address-

 

Number of bits in physical address

= Number of bits in tag + Number of bits in block offset

= 17 bits + 10 bits

= 27 bits

Thus, Number of bits in physical address = 27 bits

 

 

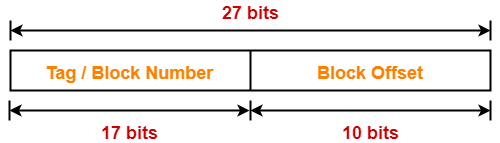
Size of Main Memory-

 

We have,

Number of bits in physical address = 27 bits

Thus, Size of main memory

= 2²⁷ bytes

= 128 MB

 

Number of Lines in Cache-

 

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 512 lines

= 2⁹ lines

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁹ x 17 bits

= 8704 bits

= 1088 bytes

Thus, size of tag directory = 1088 bytes

 

Also Read- Practice Problems On Set Associative Mapping

 

Problem-03:

 

Consider a fully associative mapped cache with block size 4 KB. The size of main memory is 16 GB. Find the number of bits in tag.

 

Solution-

 

Given-

• Block size = Frame size = Line size = 4 KB
• Size of main memory = 16 GB

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

 

 

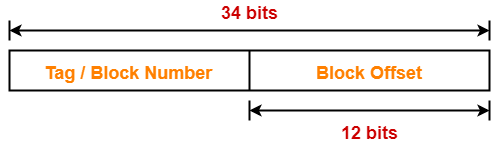
Number of Bits in Block Offset-

 

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

 

 

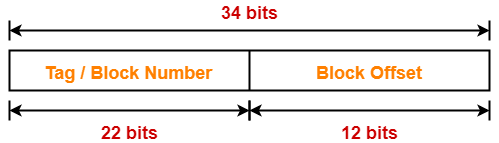
Number of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 34 bits – 12 bits

= 22 bits

Thus, Number of bits in tag = 22 bits

 

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Next Article- Set Associative Mapping | Implementation & Formulas

 

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.