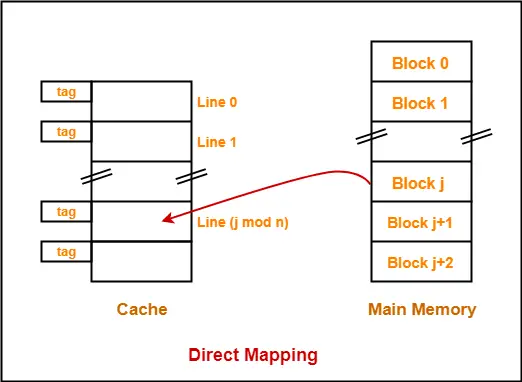
Direct Mapping | Cache | Practice Problems

Direct Mapping-

 

Before you go through this article, make sure that you have gone through the previous article on Direct Mapping.

 

In direct mapping,

• A particular block of main memory can be mapped to one particular cache line only.
• Block ‘j’ of main memory will map to line number (j mod number of cache lines) of the cache.
• There is no need of any replacement algorithm.

 

In this article, we will discuss practice problems based on direct mapping.

 

Also Read- Cache Mapping Techniques

 

PRACTICE PROBLEMS BASED ON DIRECT MAPPING-

 

Problem-01:

 

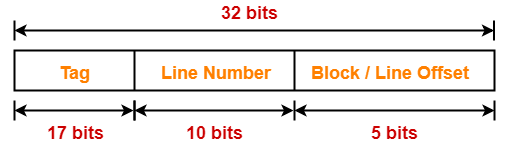
Consider a direct mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

1. Number of bits in tag
2. Tag directory size

 

Solution-

 

Given-

• Cache memory size = 16 KB
• Block size = Frame size = Line size = 256 bytes
• Main memory size = 128 KB

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

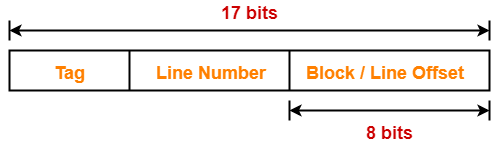
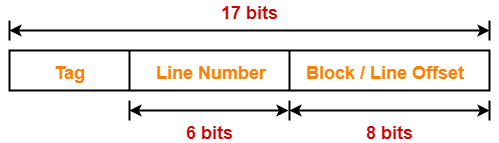
Thus, Number of bits in physical address = 17 bits

 

 

Number of Bits in Block Offset-

 

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

 

 

Number of Bits in Line Number-

 

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 2⁶ lines

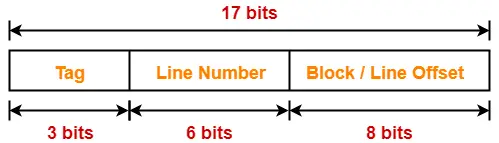
Thus, Number of bits in line number = 6 bits

 

 

Number of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 17 bits – (6 bits + 8 bits)

= 17 bits – 14 bits

= 3 bits

Thus, Number of bits in tag = 3 bits

 

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁶ x 3 bits

= 192 bits

= 24 bytes

Thus, size of tag directory = 24 bytes

 

Problem-02:

 

Consider a direct mapped cache of size 512 KB with block size 1 KB. There are 7 bits in the tag. Find-

1. Size of main memory
2. Tag directory size

 

Solution-

 

Given-

• Cache memory size = 512 KB
• Block size = Frame size = Line size = 1 KB
• Number of bits in tag = 7 bits

 

We consider that the memory is byte addressable.

 

Number of Bits in Block Offset-

 

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

 

 

Number of Bits in Line Number-

 

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 2⁹ lines

Thus, Number of bits in line number = 9 bits

 

 

Number of Bits in Physical Address-

 

Number of bits in physical address

= Number of bits in tag + Number of bits in line number + Number of bits in block offset

= 7 bits + 9 bits + 10 bits

= 26 bits

Thus, Number of bits in physical address = 26 bits

 

Size of Main Memory-

 

We have,

Number of bits in physical address = 26 bits

Thus, Size of main memory

= 2²⁶ bytes

= 64 MB

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁹ x 7 bits

= 3584 bits

= 448 bytes

Thus, size of tag directory = 448 bytes

 

Problem-03:

 

Consider a direct mapped cache with block size 4 KB. The size of main memory is 16 GB and there are 10 bits in the tag. Find-

1. Size of cache memory
2. Tag directory size

 

Solution-

 

Given-

• Block size = Frame size = Line size = 4 KB
• Size of main memory = 16 GB
• Number of bits in tag = 10 bits

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

 

 

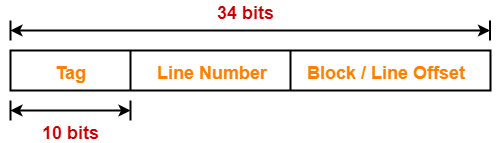
Number of Bits in Block Offset-

 

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

 

 

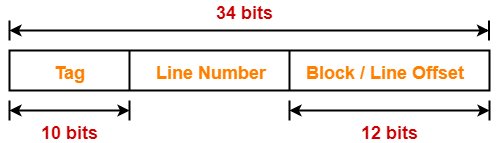
Number of Bits in Line Number-

 

Number of bits in line number

= Number of bits in physical address – (Number of bits in tag + Number of bits in block offset)

= 34 bits – (10 bits + 12 bits)

= 34 bits – 22 bits

= 12 bits

Thus, Number of bits in line number = 12 bits

 

 

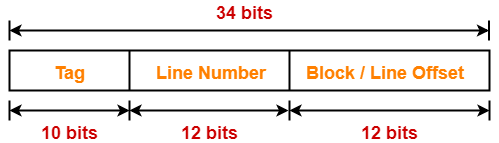
Number of Lines in Cache-

 

We have-

Number of bits in line number = 12 bits

Thus, Total number of lines in cache = 2¹² lines

 

Size of Cache Memory-

 

Size of cache memory

= Total number of lines in cache x Line size

= 2¹² x 4 KB

= 2¹⁴ KB

= 16 MB

Thus, Size of cache memory = 16 MB

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2¹² x 10 bits

= 40960 bits

= 5120 bytes

Thus, size of tag directory = 5120 bytes

 

Also Read- Practice Problems On Set Associative Mapping

 

Problem-04:

 

Consider a direct mapped cache of size 32 KB with block size 32 bytes. The CPU generates 32 bit addresses. The number of bits needed for cache indexing and the number of tag bits are respectively-

1. 10, 17
2. 10, 22
3. 15, 17
4. 5, 17

 

Solution-

 

Given-

• Cache memory size = 32 KB
• Block size = Frame size = Line size = 32 bytes
• Number of bits in physical address = 32 bits

 

Number of Bits in Block Offset-

 

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

 

 

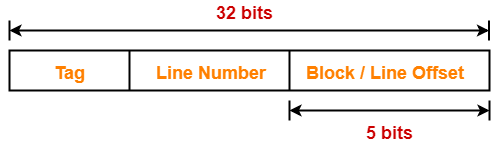
Number of Bits in Line Number-

 

Total number of lines in cache

= Cache size / Line size

= 32 KB / 32 bytes

= 2¹⁰ lines

Thus, Number of bits in line number = 10 bits

 

 

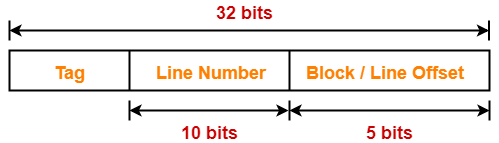
Number of Bits Required For Cache Indexing-

 

Number of bits required for cache indexing

= Number of bits in line number

= 10 bits

 

Number Of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (10 bits + 5 bits)

= 32 bits – 15 bits

= 17 bits

Thus, Number of bits in tag = 17 bits

 

 

Thus, Option (A) is correct.

 

Problem-05:

 

Consider a machine with a byte addressable main memory of 2³² bytes divided into blocks of size 32 bytes. Assume that a direct mapped cache having 512 cache lines is used with this machine. The size of the tag field in bits is ______.

 

Solution-

 

Given-

• Main memory size = 2³² bytes
• Block size = Frame size = Line size = 32 bytes
• Number of lines in cache = 512 lines

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 2³² bytes

Thus, Number of bits in physical address = 32 bits

 

 

Number of Bits in Block Offset-

 

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

 

 

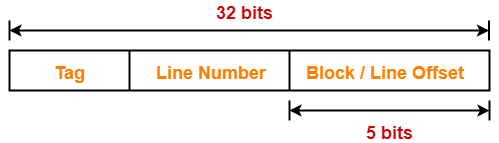
Number of Bits in Line Number-

 

Total number of lines in cache

= 512 lines

= 2⁹ lines

Thus, Number of bits in line number = 9 bits

 

 

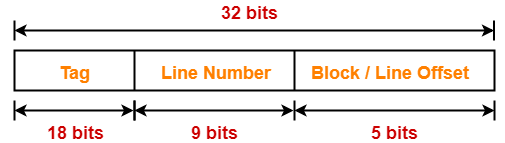
Number Of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (9 bits + 5 bits)

= 32 bits – 14 bits

= 18 bits

Thus, Number of bits in tag = 18 bits

 

 

Problem-06:

 

An 8 KB direct-mapped write back cache is organized as multiple blocks, each of size 32 bytes. The processor generates 32 bit addresses. The cache controller maintains the tag information for each cache block comprising of the following-

• 1 valid bit
• 1 modified bit
• As many bits as the minimum needed to identify the memory block mapped in the cache

What is the total size of memory needed at the cache controller to store meta data (tags) for the cache?

1. 4864 bits
2. 6144 bits
3. 6656 bits
4. 5376 bits

 

Solution-

 

Given-

• Cache memory size = 8 KB
• Block size = Frame size = Line size = 32 bytes
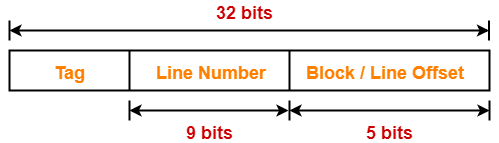
• Number of bits in physical address = 32 bits

 

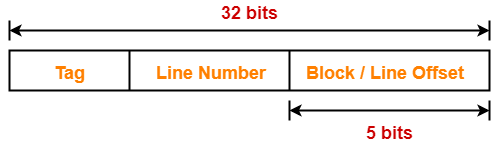
Number of Bits in Block Offset-

 

We have,

Block size

= 32 bytes

= 2⁵ bytes

Thus, Number of bits in block offset = 5 bits

 

 

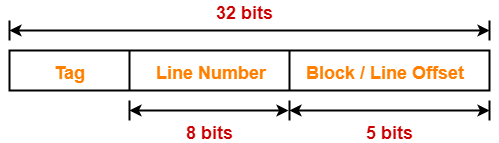
Number of Bits in Line Number-

 

Total number of lines in cache

= Cache memory size / Line size

= 8 KB / 32 bytes

= 2¹³ bytes / 2⁵ bytes

= 2⁸ lines

Thus, Number of bits in line number = 8 bits

 

 

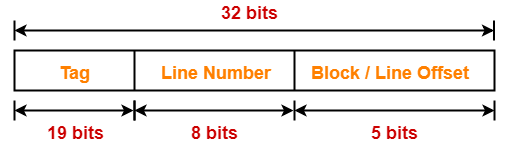
Number Of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)

= 32 bits – (8 bits + 5 bits)

= 32 bits – 13 bits

= 19 bits

Thus, Number of bits in tag = 19 bits

 

 

Memory Size Needed At Cache Controller-

 

Size of memory needed at cache controller

= Number of lines in cache x (1 valid bit + 1 modified bit + 19 bits to identify block)

= 2⁸ x 21 bits

= 5376 bits

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Next Article- Practice Problems On Fully Associative Mapping

 

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.