Depth First Search-
- Depth First Search or DFS is a graph traversal algorithm.
- It is used for traversing or searching a graph in a systematic fashion.
- DFS uses a strategy that searches “deeper” in the graph whenever possible.
- Stack data structure is used in the implementation of depth first search.
DFS Example-
Consider the following graph-
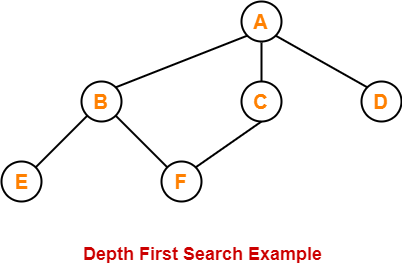
The depth first search traversal order of the above graph is-
A, B, E, F, C, D
Depth First Search Algorithm-
DFS (V,E)
for each vertex u in V[G]
do color[v] ← WHITE
π[v] ← NIL
time ← 0
for each vertex v in V[G]
do if color[v] ← WHITE
then Depth_First_Search(v)
Depth_First_Search (v)
color[v] ← GRAY
time ← time + 1
d[v] ← time
for each vertex u adjacent to v
do if color[u] ← WHITE
π[u] ← v
Depth_First_Search(u)
color[v] ← BLACK
time ← time + 1
f[v] ← time
Explanation-
The above depth first search algorithm is explained in the following steps-
Step-01
Create and maintain 4 variables for each vertex of the graph. For any vertex ‘v’ of the graph, these 4 variables are-
1. color[v]-
2. Π[v]-
This variable represents the predecessor of vertex ‘v’.
3. d[v]-
This variable represents a timestamp when a vertex ‘v’ is discovered.
3. f[v]-
This variable represents a timestamp when the processing of vertex ‘v’ is completed.
Step-02
For each vertex of the graph, initialize the variables as-
Step-03
Repeat the following procedure until all the vertices of the graph become BLACK- Consider any white vertex ‘v’ and call the following Depth_First_Search function on it.
Depth_First_Search (G,v)
1. color[v] = GRAY 2. time = time + 1 3. d[v] = time 4. For each adjacent WHITE vertex ‘u’ of ‘v’, set π[u] = v and call Depth_First_Search (G,u) 5. color[v] = BLACK 6. time = time + 1 7. f[v] = time |
DFS Time Complexity-
The total running time for Depth First Search is θ (V+E).
Types of Edges in DFS-
After a DFS traversal of any graph G, all its edges can be put in one of the following 4 classes-
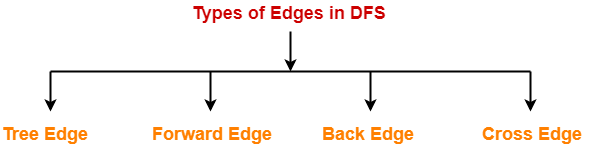
- Tree Edge
- Back Edge
- Forward Edge
- Cross Edge
1. Tree Edge-
- A tree edge is an edge that is included in the DFS tree.
2. Back Edge-
| An edge from a vertex ‘u’ to one of its ancestors ‘v’ is called as a back edge.
A self-loop is considered as a back edge. |
A back edge is discovered when-
- DFS tries to extend the visit from a vertex ‘u’ to vertex ‘v’
- And vertex ‘v’ is found to be an ancestor of vertex ‘u’ and grey at that time.
3. Forward Edge-
| An edge from a vertex ‘u’ to one of its descendants ‘v’ is called as a forward edge. |
A forward edge is discovered when-
- DFS tries to extend the visit from a vertex ‘u’ to a vertex ‘v’
- And finds that color(v) = BLACK and d(v) > d(u).
4. Cross Edge-
| An edge from a vertex ‘u’ to a vertex ‘v’ that is neither its ancestor nor its descendant is called as a cross edge. |
A cross edge is discovered when-
- DFS tries to extend the visit from a vertex ‘u’ to a vertex ‘v’
- And finds that color(v) = BLACK and d(v) < d(u).
PRACTICE PROBLEM BASED ON DEPTH FIRST SEARCH-
Problem-
Compute the DFS tree for the graph given below-
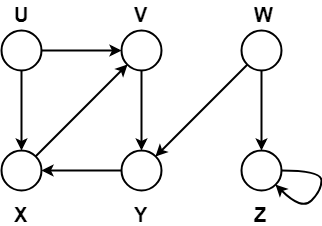
Also, show the discovery and finishing time for each vertex and classify the edges.
Solution-
Initially for all the vertices of the graph, we set the variables as-
- color[v] = WHITE
- π[v] = NIL
- time = 0 (Global)
Let us start processing the graph from vertex U.
Step-01:
- color[U] = GREY
- time = 0 + 1 = 1
- d[U] = 1

Step-02:
- π[V] = U
- color[V] = GREY
- time = 1 + 1 = 2
- d[V] = 2
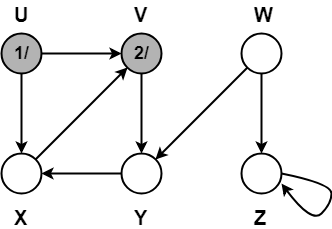
Step-03:
- π[Y] = V
- color[Y] = GREY
- time = 2 + 1 = 3
- d[Y] = 3
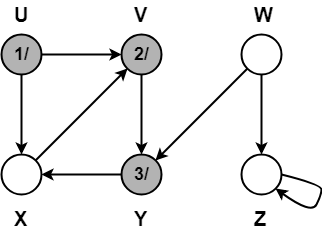
Step-04:
- π[X] = Y
- color[X] = GREY
- time = 3 + 1 = 4
- d[X] = 4
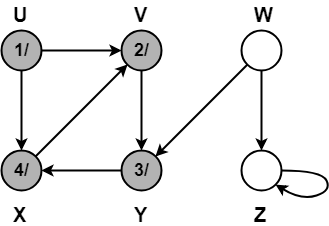
Step-05:
When DFS tries to extend the visit from vertex X to vertex V, it finds-
- Vertex V is an ancestor of vertex X since it has already been discovered
- Vertex V is GREY in color.
Thus, edge XV is a back edge.
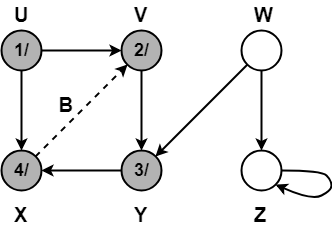
Step-06:
- color[X] = BLACK
- time = 4 + 1 = 5
- f[X] = 5
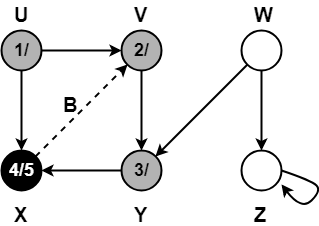
Step-07:
- color[Y] = BLACK
- time = 5 + 1 = 6
- f[Y] = 6
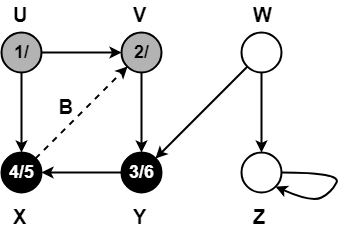
Step-08:
- color[V] = BLACK
- time = 6 + 1 = 7
- f[V] = 7
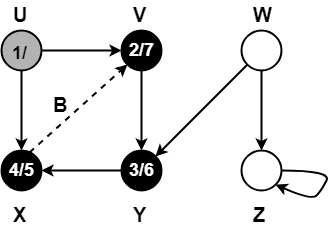
Step-09:
When DFS tries to extend the visit from vertex U to vertex X, it finds-
- Vertex X has already been completely processed i.e. vertex X has finished and is black.
- But vertex U has still not finished.
Alternatively,
When DFS tries to extend the visit from vertex U to vertex X, it finds-
- Color(X) = BLACK
- d(X) > d(U)
Thus, edge UX is a forward edge.
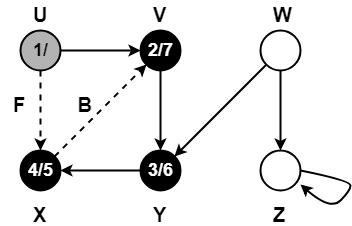
Step-10:
- color[U] = BLACK
- time = 7 + 1 = 8
- f[U] = 8
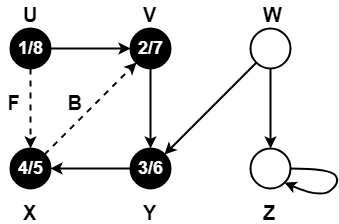
Step-11:
- color[W] = GREY
- time = 8 + 1 = 9
- d[W] = 9
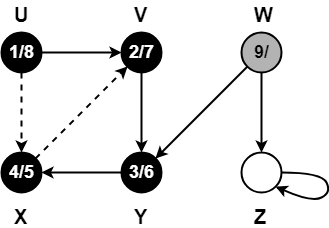
Step-12:
When DFS tries to extend the visit from vertex W to vertex Y, it finds-
- Vertex Y has already been completely processed i.e. vertex Y has finished.
- Vertex Y is neither a descendant nor an ancestor of vertex W.
Alternatively,
When DFS tries to extend the visit from vertex W to vertex Y, it finds-
- Color(Y) = BLACK
- d(Y) < d(W)
Thus, edge WY is a cross edge.
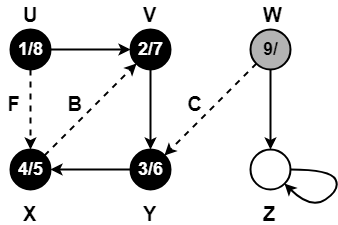
Step-13:
- π[Z] = W
- color[W] = GREY
- time = 9 + 1 = 10
- d[W] = 10
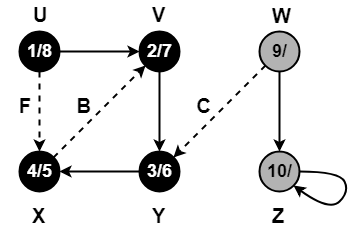
Step-14:
Since, self-loops are considered as back edges.
Therefore, self-loop present on vertex Z is considered as a back edge.
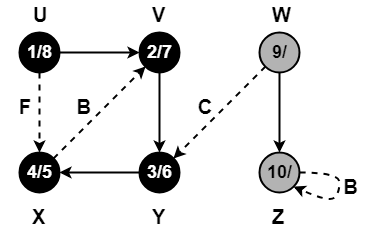
Step-15:
- color[Z] = BLACK
- time = 10 + 1 = 11
- f[Z] = 11
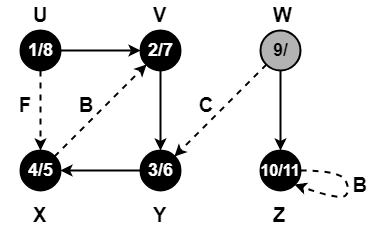
Step-16:
- color[W] = BLACK
- time = 11 + 1 = 12
- f[W] = 12
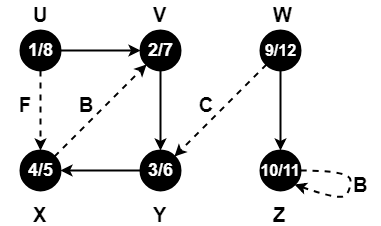
Since all the vertices have turned black, so we stop.
This is how a given graph is traversed using Depth First Search (DFS) technique.
To gain better understanding about Depth First Search Algorithm,
Next Article- Breadth First Search
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.

