CYK Algorithm-
| CYK Algorithm is a membership algorithm of context free grammar. |
- It is used to decide whether a given string belongs to the language of grammar or not.
- It is also known as CKY Algorithm or Cocke-Younger-Kasami Algorithm after its inventors.
Important Notes-
Note-01:
Note-02:
- The worst case running time of CYK Algorithm is Θ (n3.|G|).
- Here, n = Length of parsed string and |G| = Size of the CNF Grammar G.
Algorithm-
Begin
for ( i = 1 to n do )
Vi1 { A | A → a is a production where ith symbol of x is a }
for ( j = 2 to n do )
for ( i = 1 to n - j + 1 do )
Begin
Vij = ϕ
For k = 1 to j - 1 do
Vij = Vij ∪ { A | A → BC is a production where B is in Vik and C is in V(i + k)(j - k) }
End
End
Also Read- Algorithm To Check Whether CFL is Empty
Deciding Membership Using CYK Algorithm-
To decide the membership of any given string, we construct a triangular table where-
- Each row of the table corresponds to one particular length of sub strings.
- Bottom most row corresponds to strings of length-1.
- Second row from bottom corresponds to strings of length-2.
- Third row from bottom corresponds to strings of length-3.
- Top most row from bottom corresponds to the given string of length-n.
Example-
For a given string “x” of length 4 units, triangular table looks like-
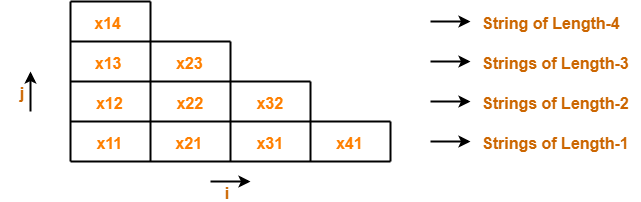
We will fill each box of xij with its Vij.
These notations are discussed below.
Notations Used
Notation-01: xij
xij represents a sub string of “x” starting from location ‘i’ and has length ‘j’.
Example-
Consider x = abcd is a string, then-
Number of sub strings possible = n(n+1)/2 = 4 x (4+1) / 2 = 10
We have-
- x11 = a
- x21 = b
- x31 = c
- x41 = d
- x12 = ab
- x22 = bc
- x32 = cd
- x13 = abc
- x23 = bcd
- x14 = abcd
Notation-02: Vij
Vij represents a set of variables in the grammar which can derive the sub string xij.
If the set of variables consists of the start symbol, then it becomes sure-
- Sub string xij can be derived from the given grammar.
- Sub string xij is a member of the language of the given grammar.
|
Also Read- Algorithm To Check Whether CFL is Finite
PRACTICE PROBLEM BASED ON CYK ALGORITHM-
Problem-
For the given grammar, check the acceptance of string w = baaba using CYK Algorithm-
S → AB / BC
A → BA / a
B → CC / b
C → AB / a
Solution-
First, let us draw the triangular table.
- The given string is x = baaba.
- Length of given string = |x| = 5.
- So, Number of sub strings possible = (5 x 6) / 2 = 15.
So, triangular table looks like-
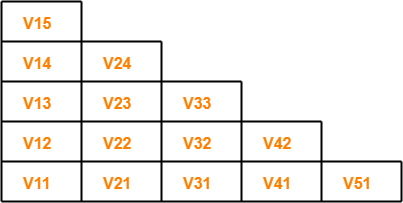
Now, let us find the value of Vij for each cell.
For Row-1:
Finding V11
- V11 represents the set of variables deriving x11.
- x11 = b.
- Only variable B derives string “b” in the given grammar.
- Thus, V11 = { B }
Finding V21
- V21 represents the set of variables deriving x21.
- x21 = a.
- Variables A and C derive string “a” in the given grammar.
- Thus, V21 = { A , C }
Finding V31
- V31 represents the set of variables deriving x31.
- x31 = a.
- Variables A and C derive string “b” in the given grammar.
- Thus, V31 = { A , C }
Finding V41
- V41 represents the set of variables deriving x41.
- x41 = b.
- Only variable B derives string “b” in the given grammar.
- Thus, V41 = { B }
Finding V51
- V51 represents the set of variables deriving x51.
- x51 = a.
- Variables A and C derives string “a” in the given grammar.
- Thus, V51 = { A , C }
For Row-2-
RULE
As per the algorithm, to find the value of Vij from 2nd row on wards,
we use the formula-
Vij = Vik V(i+k)(j-k)
where k varies from 1 to j-1
|
Finding V12
We have i = 1 , j = 2 , k = 1
Substituting values in the formula, we get-
V12 = V11. V21
V12 = { B } { A , C }
V12 = { BA , BC }
∴ V12 = { A , S }
Finding V22
We have i = 2 , j = 2 , k = 1
Substituting values in the formula, we get-
V22 = V21. V31
V22 = { A , C } { A , C }
V22 = { AA , AC , CA , CC }
Since AA , AC and CA do not exist, so we have-
V22 = { CC }
∴ V22 = { B }
Finding V32
We have i = 3 , j = 2 , k = 1
Substituting values in the formula, we get-
V32 = V31. V41
V32 = { A , C } { B }
V32 = { AB , CB }
Since CB does not exist, so we have-
V32 = { AB }
∴ V32 = { S , C }
Finding V42
We have i = 4 , j = 2 , k = 1
Substituting values in the formula, we get-
V42 = V41. V51
V42 = { B } { A , C }
V42 = { BA , BC }
∴ V42 = { A , S }
For Row-3-
Finding V13
We have i = 1 , j = 3 , k = 1 to (3-1) = 1,2
Substituting values in the formula, we get-
V13 = V11. V22 ∪ V12. V31
V13 = { B } { B } ∪ { A , S } { A , C }
V13 = { BB } ∪ { AA , AC , SA , SC }
Since BB , AA , AC , SA and SC do not exist, so we have-
V13 = ϕ ∪ ϕ
∴ V13 = ϕ
Finding V23
We have i = 2 , j = 3 , k = 1 to (3-1) = 1,2
Substituting values in the formula, we get-
V23 = V21. V32 ∪ V22. V41
V23 = { A , C } { S , C } ∪ { B } { B }
V23 = { AS , AC , CS , CC } ∪ { BB }
Since AS , AC , CS and BB do not exist, so we have-
V23 = { CC }
∴ V23 = B
Finding V33
We have i = 3 , j = 3 , k = 1 to (3-1) = 1,2
Substituting values in the formula, we get-
V33 = V31. V42 ∪ V32. V51
V33 = { A , C } { A , S } ∪ { S , C } { A , C }
V33 = { AA , AS , CA , CS } ∪ { SA , SC , CA , CC }
Since AA , AS , CA , CS , SA , SC and CA do not exist, so we have-
V33 = ϕ ∪ { CC }
V33 = ϕ ∪ { B }
∴ V33 = { B }
For Row-4-
Finding V14
We have i = 1 , j = 4 , k = 1 to (4-1) = 1,2,3
Substituting values in the formula, we get-
V14 = V11. V23 ∪ V12. V32 ∪ V13. V41
V14 = { B } { B } ∪ { A , S } { S , C } ∪ { ϕ , B }
V14 = { BB } ∪ { AS , AC , SS , SC } ∪ { B }
Since BB , AS , AC , SS , SC and B do not exist, so we have-
V14 = ϕ ∪ ϕ ∪ ϕ
∴ V14 = ϕ
Finding V24
We have i = 2 , j = 4 , k = 1 to (4-1) = 1,2,3
Substituting values in the formula, we get-
V24 = V21. V33 ∪ V22. V42 ∪ V23. V51
V24 = { A , C } { B } ∪ { B } { A , S } ∪ { B } { A , C }
V24 = { AB , CB } ∪ { BA , BS } ∪ { BA , BC }
Since CB does not exist, so we have-
V24 = { AB } ∪ { BA , BS } ∪ { BA , BC }
V24 = { S , C } ∪ { A } ∪ { A , S }
∴ V24 = { S , C , A }
For Row-5-
Finding V15
We have i = 1 , j = 5 , k = 1 to (5-1) = 1,2,3,4
Substituting values in the formula, we get-
V15 = V11. V24 ∪ V12. V33 ∪ V13. V42 ∪ V14. V51
V15 = { B } { S , C , A } ∪ { A , S } { B } ∪ { ϕ } { A , S } ∪ { ϕ } { A , C }
V15 = { BS , BC , BA } ∪ { AB , SB } ∪ { A , S } ∪ { A , C }
Since BS , SB , A , S and C do not exist, so we have-
V15 = { BC , BA } ∪ { AB } ∪ ϕ ∪ ϕ
V15 = { S , A } ∪ { S , C } ∪ ϕ ∪ ϕ
∴ V15 = { S , A , C }
Now,
- The value of Vij is computed for each cell.
- We observe V15 contains the start symbol S.
- Thus, string x15 = baaba is a member of the language of given grammar.
After filling the triangular table, it looks like-
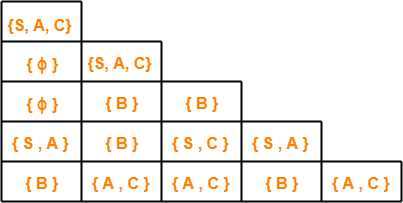
Results From Triangular Table-
The following important results can be made from the above triangular table-
Result-01:
- There exists total 4 distinct sub strings which are members of the language of given grammar.
- These 4 sub strings are ba, ab, aaba, baaba.
- This is because they contain start symbol in their respective cell.
Result-02:
- Strings which can not be derived from any variable are baa, baab.
- This is because they contain ϕ in their respective cell.
Result-03:
- Strings which can be derived from variable B alone are b, aa, aba, aab.
- This is because they contain variable B alone in their respective cell.
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.