Theory of Automata & Computation | Gate Vidyalay

Parse Tree | Derivations | Automata

Theory of Automata & Computation

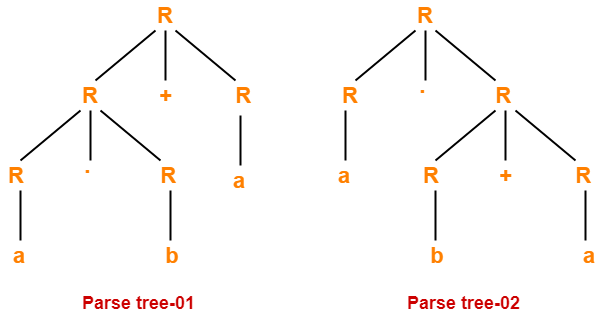
Parse Tree-

The process of deriving a string is called as derivation.
The geometrical representation of a derivation is called as a parse tree or derivation tree.

1. Leftmost Derivation-

The process of deriving a string by expanding the leftmost non-terminal at each step is called as leftmost derivation.
The geometrical representation of leftmost derivation is called as a leftmost derivation tree.

Example-

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

Now, let us derive the string w using leftmost derivation.

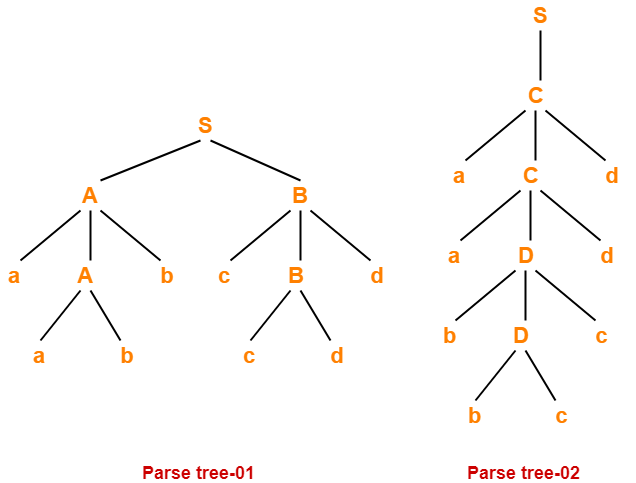
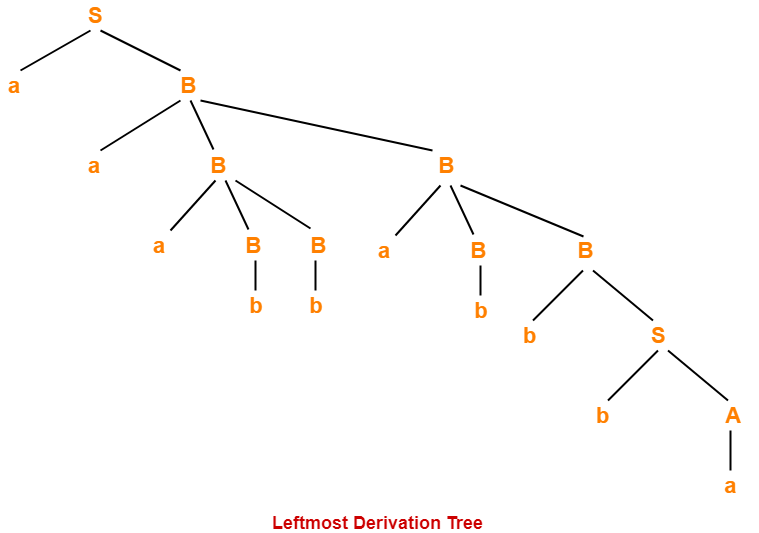
Leftmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaaBBB (Using B → aBB)

→ aaabBB (Using B → b)

→ aaabbB (Using B → b)

→ aaabbaBB (Using B → aBB)

→ aaabbabB (Using B → b)

→ aaabbabbS (Using B → bS)

→ aaabbabbbA (Using S → bA)

→ aaabbabbba (Using A → a)

2. Rightmost Derivation-

The process of deriving a string by expanding the rightmost non-terminal at each step is called as rightmost derivation.
The geometrical representation of rightmost derivation is called as a rightmost derivation tree.

Example-

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

Now, let us derive the string w using rightmost derivation.

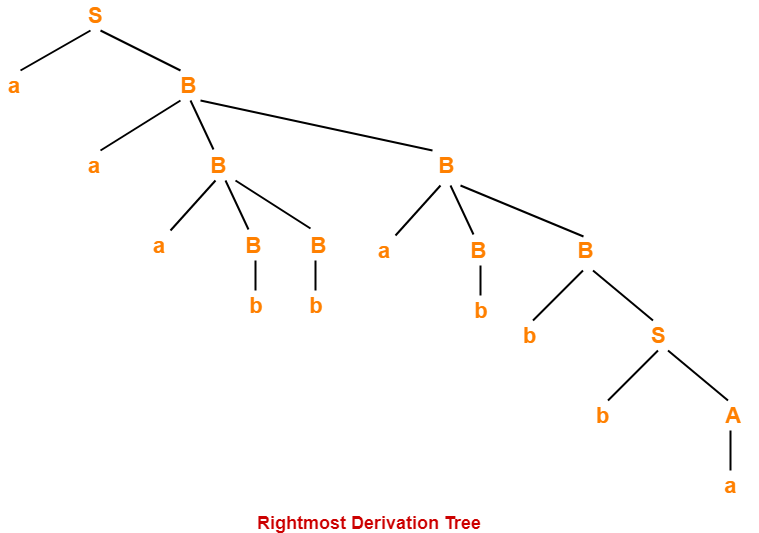
Rightmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaBaBB (Using B → aBB)

→ aaBaBbS (Using B → bS)

→ aaBaBbbA (Using S → bA)

→ aaBaBbba (Using A → a)

→ aaBabbba (Using B → b)

→ aaaBBabbba (Using B → aBB)

→ aaaBbabbba (Using B → b)

→ aaabbabbba (Using B → b)

NOTES

For unambiguous grammars, Leftmost derivation and Rightmost derivation represents the same parse tree.
For ambiguous grammars, Leftmost derivation and Rightmost derivation represents different parse trees.

Here,

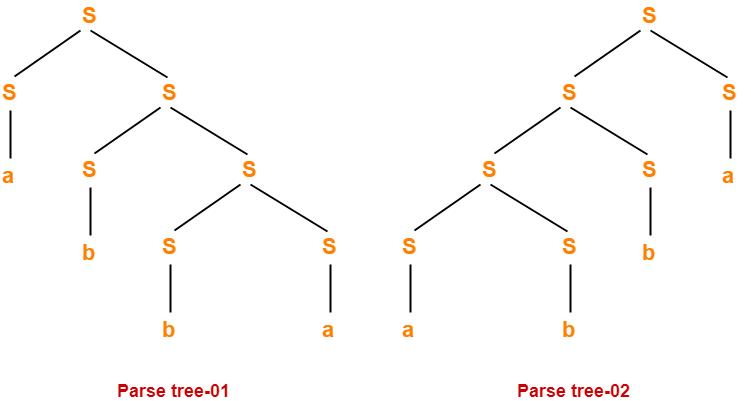
The given grammar was unambiguous.
That is why, leftmost derivation and rightmost derivation represents the same parse tree.

Leftmost Derivation Tree = Rightmost Derivation Tree

Also Read- Ambiguous Grammar

Properties Of Parse Tree-

Root node of a parse tree is the start symbol of the grammar.
Each leaf node of a parse tree represents a terminal symbol.
Each interior node of a parse tree represents a non-terminal symbol.
Parse tree is independent of the order in which the productions are used during derivations.

Yield Of Parse Tree-

Concatenating the leaves of a parse tree from the left produces a string of terminals.
This string of terminals is called as yield of a parse tree.

PRACTICE PROBLEMS BASED ON DERIVATIONS AND PARSE TREE-

Problem-01:

Consider the grammar-

S → bB / aA

A → b / bS / aAA

B → a / aS / bBB

For the string w = bbaababa, find-

Leftmost derivation
Rightmost derivation
Parse Tree

Solution-

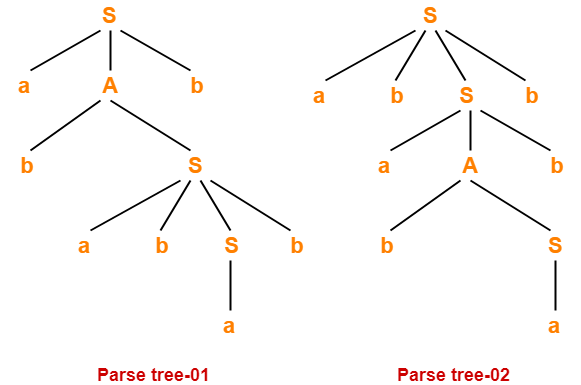
1. Leftmost Derivation-

S → bB

→ bbBB (Using B → bBB)

→ bbaB (Using B → a)

→ bbaaS (Using B → aS)

→ bbaabB (Using S → bB)

→ bbaabaS (Using B → aS)

→ bbaababB (Using S → bB)

→ bbaababa (Using B → a)

2. Rightmost Derivation-

S → bB

→ bbBB (Using B → bBB)

→ bbBaS (Using B → aS)

→ bbBabB (Using S → bB)

→ bbBabaS (Using B → aS)

→ bbBababB (Using S → bB)

→ bbBababa (Using B → a)

→ bbaababa (Using B → a)

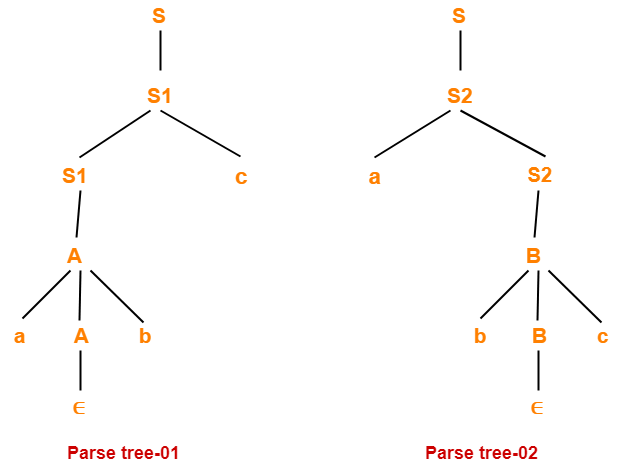
3. Parse Tree-

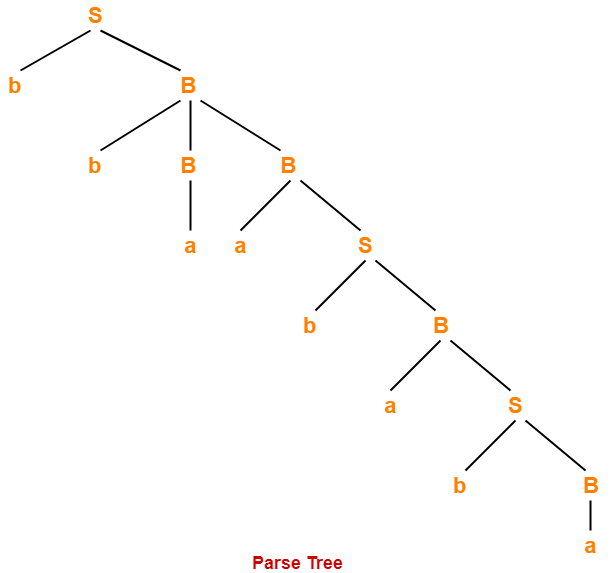
Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
The reason is given grammar is unambiguous.

Problem-02:

Consider the grammar-

S → A1B

A → 0A / ∈

B → 0B / 1B / ∈

For the string w = 00101, find-

Leftmost derivation
Rightmost derivation
Parse Tree

Solution-

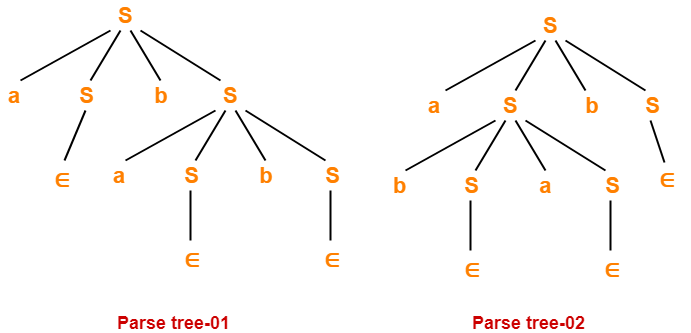
1. Leftmost Derivation-

S → A1B

→ 0A1B (Using A → 0A)

→ 00A1B (Using A → 0A)

→ 001B (Using A → ∈)

→ 0010B (Using B → 0B)

→ 00101B (Using B → 1B)

→ 00101 (Using B → ∈)

2. Rightmost Derivation-

S → A1B

→ A10B (Using B → 0B)

→ A101B (Using B → 1B)

→ A101 (Using B → ∈)

→ 0A101 (Using A → 0A)

→ 00A101 (Using A → 0A)

→ 00101 (Using A → ∈)

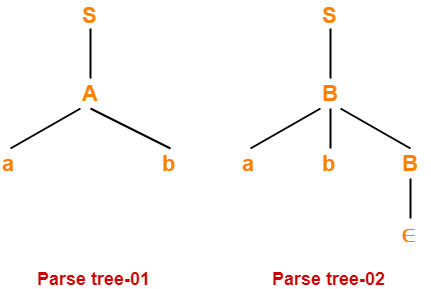
3. Parse Tree-

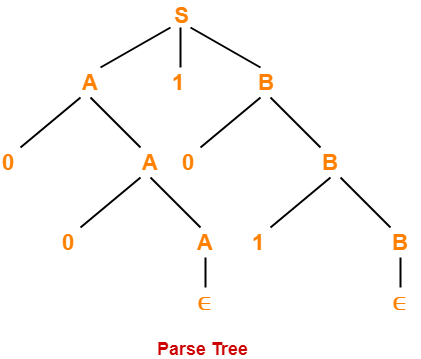
Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
The reason is given grammar is unambiguous.

To gain better understanding about Derivations and Parse Tree,

Watch this Video Lecture

Next Article- Elimination of Left Recursion

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Recursive Grammar | Left Recursive Grammar

Theory of Automata & Computation

Grammar in Automata-

Before you go through this article, make sure that you have gone through the previous article on Types of Grammar in Automata.

On the basis of number of strings, grammars are classified as-

Recursive Grammar
Non-Recursive Grammar

1. Recursive Grammar-

A grammar is said to be recursive if it contains at least one production that has the same variable at both its LHS and RHS.

OR

A grammar is said to be recursive if and only if it generates infinite number of strings.

A recursive grammar may be either-

Left recursive grammar
Right recursive grammar

A) Left Recursive Grammar-

A recursive grammar is said to be left recursive if the leftmost variable of RHS is same as variable of LHS.

OR

A recursive grammar is said to be left recursive if it has Left Recursion.

Example-

S → Sa / b

(Left Recursive Grammar)

B) Right Recursive Grammar-

A recursive grammar is said to be right recursive if the rightmost variable of RHS is same as variable of LHS.

OR

A recursive grammar is said to be right recursive if it has right recursion.

Example-

S → aS / b

(Right Recursive Grammar)

2. Non-Recursive Grammar-

A grammar is said to be non-recursive if it contains no production that has the same variable at both its LHS and RHS.

OR

A grammar is said to be non-recursive if and only if it generates finite number of strings.

NOTE

A non-recursive grammar has neither left recursion nor right recursion.

Example-

S → aA / bB

A → a / b

B → c / d

(Non-Recursive Grammar)

The language generated from this grammar is L = { aa , ab , bc , bd }

Since the grammar generates finite number of strings, therefore it is a non-recursive grammar.

Also Read- Ambiguous Grammar

Important Notes-

Note-01:

The grammar which is either left recursive or right recursive is always unambiguous.

Examples-

S → aS / b (Unambiguous Grammar)
S → Sa / b (Unambiguous Grammar)

Note-02:

The grammar which is both left recursive and right recursive is always ambiguous.

Example-

E → E + E / E – E / E x E / id

(Ambiguous Grammar)

Note-03:

Left recursive grammar is not suitable for Top down parsers.
This is because it makes the parser enter into an infinite loop.
To avoid this situation, it is converted into its equivalent right recursive grammar.
This is done by eliminating left recursion from the left recursive grammar.

Note-04:

The conversion of left recursive grammar into right recursive grammar and vice-versa is decidable.

To gain better understanding about Recursive Grammar,

Watch this Video Lecture

Next Article- Ambiguous Vs Unambiguous Grammar

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Language Ambiguity | Ambiguous Language

Theory of Automata & Computation

Language Of Grammar-

Before you go through this article, make sure that you have gone through the previous article on Language of Grammar.

We have discussed-

Language of grammar is the set of all strings that can be generated from that grammar.
Finite language consists of finite number of strings.
Infinite language consists of infinite number of strings.

In this article, we will discuss about Language Ambiguity.

Language Ambiguity-

If every grammar that generates language L is ambiguous,

then language L is called as Inherently ambiguous language.

OR

A language is inherently ambiguous if all the grammars which generate that language are ambiguous.

Also Read- Ambiguous Grammar

NOTE-

The term “inherently ambiguous language” is used instead of “ambiguous language”.
This is because all the grammars which generate that language are ambiguous.

Important Points-

If a grammar is ambiguous, it does not imply that its language will be ambiguous too.
If a grammar is ambiguous, its language may be unambiguous.
If a grammar is ambiguous, its language will be unambiguous when there exists at least one unambiguous grammar which generates that language.

Example Of Not An Inherently Ambiguous Language-

Consider the following language-

L = aⁿ , n>=0

This language consists of strings having any number of a’s.
Few grammars which generate this language are-

Grammar-01:

S → aS / ∈

(Unambiguous Grammar)

Grammar-02:

S → aS / a / ∈

(Ambiguous Grammar)

Grammar-03:

S → aS / Sa / ∈

(Ambiguous Grammar)

Grammar-04:

S → aS / a / Sa / ∈

(Ambiguous Grammar)

All the above grammars generate the same language L = aⁿ , n>=0.
Grammar-01 is unambiguous.
Since there exists at least one unambiguous grammar which generates language L.
Therefore, L is not an inherently ambiguous language.

Example Of An Inherently Ambiguous Language-

Consider the following language-

L = { aⁿbⁿc^m } ∪ { aⁿb^mc^m }

There exists only one grammar which generates this language L.

The grammar is-

S → S₁ / S₂

S₁ → S₁C / A

A → aAb / ∈

S₂ → aS₂ / B

B → bBc / ∈

This grammar is ambiguous in nature.

This is because following two parse trees exist for string w = abc-

Also Read- Checking Grammar Ambiguity

There exists no language that generates this language L and is unambiguous.
Therefore, L is an inherently ambiguous language.

Next Article- Context Free Grammar

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Grammar Ambiguity | Check Ambiguous Grammar

Theory of Automata & Computation

Grammar Ambiguity-

Before you go through this article, make sure that you have gone through the previous article on Ambiguous Grammar.

There exists no algorithm to check whether any given grammar is ambiguous or not.
This general decision problem is undecidable-

“Whether a grammar is ambiguous or not?”

This is because it can be shown that this problem is equivalent to Post Correspondence Problem.

General Approach To Check Grammar Ambiguity-

To check whether a given grammar is ambiguous or not, we follow the following steps-

Step-01:

We try finding a string from the Language of Grammar such that for the string there exists more than one-

parse tree
or derivation tree
or syntax tree
or leftmost derivation
or rightmost derivation

Step-02:

If there exists at least one such string, then the grammar is ambiguous otherwise unambiguous.

PROBLEMS BASED ON CHECKING WHETHER GRAMMAR IS AMBIGUOUS-

Problem-01:

Check whether the given grammar is ambiguous or not-

S → SS

S → a

S → b

Solution-

Let us consider a string w generated by the given grammar-

w = abba

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-02:

Check whether the given grammar is ambiguous or not-

S → A / B

A → aAb / ab

B → abB / ∈

Solution-

Let us consider a string w generated by the given grammar-

w = ab

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-03:

Check whether the given grammar is ambiguous or not-

S → AB / C

A → aAb / ab

B → cBd / cd

C → aCd / aDd

D → bDc / bc

Solution-

Let us consider a string w generated by the given grammar-

w = aabbccdd

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-04:

Check whether the given grammar is ambiguous or not-

S → AB / aaB

A → a / Aa

B → b

Solution-

Let us consider a string w generated by the given grammar-

w = aab

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-05:

Check whether the given grammar is ambiguous or not-

S → a / abSb / aAb

A → bS / aAAb

Solution-

Let us consider a string w generated by the given grammar-

w = abababb

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-06:

Check whether the given grammar is ambiguous or not-

E → E + T / T

T → T x F / F

F → id

Solution-

There exists no string belonging to the language of grammar which has more than one parse tree.
Since a unique parse tree exists for all the strings, therefore the given grammar is unambiguous.

Problem-07:

Check whether the given grammar is ambiguous or not-

S → aSbS / bSaS / ∈

Solution-

Let us consider a string w generated by the given grammar-

w = abab

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

Problem-08:

Check whether the given grammar is ambiguous or not-

R → R + R / R . R / R* / a / b

Solution-

Let us consider a string w generated by the given grammar-

w = ab + a

Now, let us draw parse trees for this string w.

Since two different parse trees exist for string w, therefore the given grammar is ambiguous.

To gain better understanding about Grammar Ambiguity,

Watch this Video Lecture

Next Article- Converting Ambiguous into Unambiguous Grammar

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Difference between Ambiguous and Unambiguous Grammar

Theory of Automata & Computation

Difference Between Ambiguous and Unambiguous Grammar-

Before you go through this article, make sure that you have gone through the previous article on Ambiguous Grammar.

Some of the important differences between ambiguous grammar and unambiguous grammar are-

Ambiguous Grammar	Unambiguous Grammar
A grammar is said to be ambiguous if for at least one string generated by it, it produces more than one- parse tree or derivation tree or syntax tree or leftmost derivation or rightmost derivation	A grammar is said to be unambiguous if for all the strings generated by it, it produces exactly one- parse tree or derivation tree or syntax tree or leftmost derivation or rightmost derivation
For ambiguous grammar, leftmost derivation and rightmost derivation represents different parse trees.	For unambiguous grammar, leftmost derivation and rightmost derivation represents the same parse tree.
Ambiguous grammar contains less number of non-terminals.	Unambiguous grammar contains more number of non-terminals.
For ambiguous grammar, length of parse tree is less.	For unambiguous grammar, length of parse tree is large.
Ambiguous grammar is faster than unambiguous grammar in the derivation of a tree. (Reason is above 2 points)	Unambiguous grammar is slower than ambiguous grammar in the derivation of a tree.
Example- E → E + E / E x E / id (Ambiguous Grammar)	Example- E → E + T / T T → T x F / F F → id (Unambiguous Grammar)

Next Article- Algorithm To Check Grammar Ambiguity

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Category: Theory of Automata & Computation

Parse Tree-

1. Leftmost Derivation-

Example-

Leftmost Derivation-

2. Rightmost Derivation-

Example-

Rightmost Derivation-

NOTES

Properties Of Parse Tree-

Yield Of Parse Tree-

PRACTICE PROBLEMS BASED ON DERIVATIONS AND PARSE TREE-

Problem-01:

Solution-

1. Leftmost Derivation-

2. Rightmost Derivation-

3. Parse Tree-

Problem-02:

Solution-

1. Leftmost Derivation-

2. Rightmost Derivation-

3. Parse Tree-

Grammar in Automata-

1. Recursive Grammar-

A) Left Recursive Grammar-

Example-

B) Right Recursive Grammar-

Example-

2. Non-Recursive Grammar-

NOTE

Example-

Important Notes-

Note-01:

Note-02:

Note-03:

Note-04:

Language Of Grammar-

Language Ambiguity-

NOTE-

Important Points-

Example Of Not An Inherently Ambiguous Language-

Grammar-01:

Grammar-02:

Grammar-03:

Grammar-04:

Example Of An Inherently Ambiguous Language-

Grammar Ambiguity-

General Approach To Check Grammar Ambiguity-

Step-01:

Step-02:

PROBLEMS BASED ON CHECKING WHETHER GRAMMAR IS AMBIGUOUS-

Problem-01:

Solution-

Problem-02:

Solution-

Problem-03:

Solution-

Problem-04:

Solution-

Problem-05:

Solution-

Problem-06:

Solution-

Problem-07:

Solution-

Problem-08:

Solution-

Difference Between Ambiguous and Unambiguous Grammar-