Theory of Automata & Computation | Gate Vidyalay

Category: Theory of Automata & Computation

Evaluating Expressions Based On Given Grammar

Theory of Automata & Computation

Evaluating Expressions Based On Given Grammar-

There are two methods for evaluating the expressions based on given grammar-

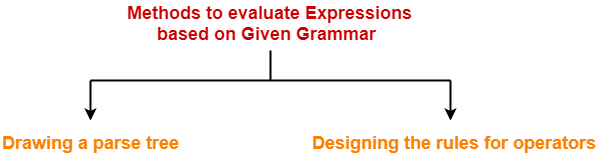
Drawing a parse tree
Designing the rules for operators

Method-01: Drawing Parse Tree-

In this method, following steps are followed-

We draw a Parse Tree for the given expression.
We evaluate the parse tree to get the required value of the expression.

Drawback-

Drawing a parse tree for large expressions is cumbersome and time taking.
So, this method becomes difficult to follow when the expression is large.

Method-02: Designing Rules For Operators-

In this method, following steps are followed-

We decide the priority and associativity of operators in the grammar.
We parenthesize the given expression.
We evaluate the expression to get the required value.

Advantage-

This method is easy to follow whether the expression is small or large.
So, this method is preferred.

Rules For Deciding Priority Of Operators-

For the given unambiguous grammar,

The priority of operators is decided by checking the level at which the production is present.
The higher the level of production, the lower the priority of operator contained in it.
The lower the level of production, the higher the priority of operator contained in it.

Also Read- Converting Ambiguous into Unambiguous Grammar

Example-

Consider the grammar-

E → E x F / F + E / F

F → F – T / T

T → id

Here,

id has the highest priority.

(since T → id is present at the bottom most level)

x and + operators have the least priority.

(since E → E x F / F + E are present at the top most level)

x and + operators have the same priority.

(since E → E x F / F + E are present at the same level)

– operator has higher priority than x and + but lesser priority than id.

(since F → F – T is present at the middle level)

So, the priority order is-

id > – > ( x , + )

Rules For Deciding Associativity Of Operators-

For the given unambiguous grammar,

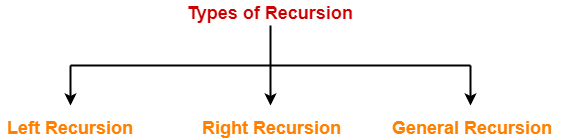
The associativity of operators is decided by checking the Type Of Recursion in the production.
If the production has left recursion, then the operator is left associative.
If the production has right recursion, then the operator is right associative.
If the production has both left and right recursion, then the operator is neither left associative nor right associative.

Example-

Consider the grammar-

E → E x F / F + E / F

F → F – F / T

T → id

Here,

x operator is left associative.

(since E → E x F has left recursion in it)

+ operator is right associative.

(since E → F + E has right recursion in it)

F – F is neither left associative nor right associative.

(since F → F – F has both left and right recursion in it)

PRACTICE PROBLEMS BASED ON EVALUATING EXPRESSIONS FOR GRAMMAR-

Problem-01:

Consider the given grammar-

E → E + T / T

T → F x T / F

F → id

Evaluate the following expression in accordance with the given grammar-

2 + 3 x 5 x 6 + 2

Solution-

Method-01:

Let us draw a parse tree for the given expression.
Evaluating the parse tree will return the required value of the expression.

The parse tree for the given expression is-

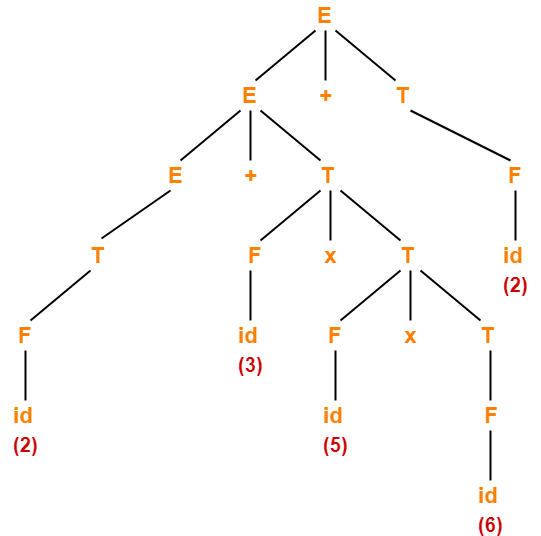
On evaluating this parse tree, we get the value = 94.

Method-02:

The priority order and associativity of operators on the basis of given grammar is-

id > x > +

where-

x operator is right associative.
+ operator is left associative.

Now, we parenthesize the given expression based on the precedence and associativity of operators as-

( 2 + ( 3 x ( 5 x 6 ) ) ) + 2

Now, we evaluate the parenthesized expression as-

= ( 2 + ( 3 x ( 5 x 6 ) ) ) + 2

= ( 2 + ( 3 x 30 ) ) + 2

= ( 2 + 90 ) + 2

= 92 + 2

= 94

Problem-02:

Consider the given grammar-

E → E + T / E – T / T

T → T x F / T ÷ F / F

F → G ↑ F / G

G → id

Evaluate the following expression in accordance with the given grammar-

2 x 1 + 4 ↑ 2 ↑ 1 x 1 + 3

Solution-

Method-01:

Let us draw a parse tree for the given expression.
Evaluating the parse tree will return the required value of the expression.

The parse tree for the given expression is-

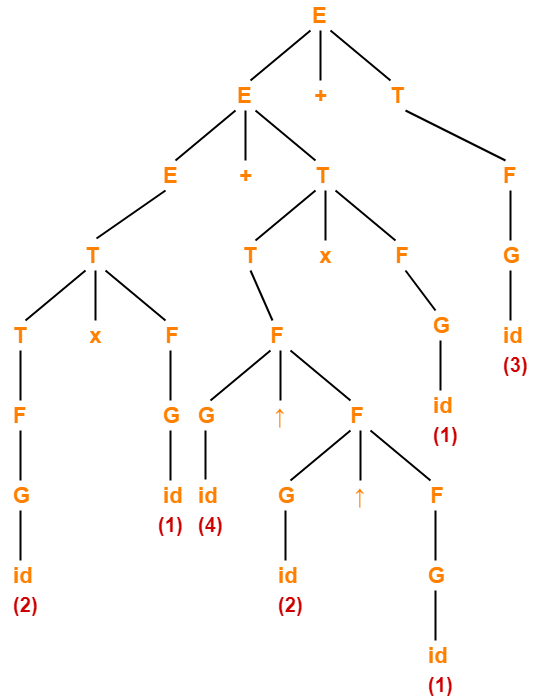
On evaluating this parse tree, we get the value = 21.

Method-02:

The priority order and associativity of operators on the basis of given grammar is-

id > ↑ > ( x , ÷ ) > ( + , – )

where-

+ , – , x , ÷ operators are left associative.
↑ operator is right associative

Now, we parenthesize the given expression based on the precedence and associativity of operators as-

( ( 2 x 1 ) + ( ( 4 ↑ ( 2 ↑ 1 ) ) x 1 ) ) + 3

Now, we evaluate the parenthesized expression as-

= ( ( 2 x 1 ) + ( ( 4 ↑ ( 2 ↑ 1 ) ) x 1 ) ) + 3

= ( ( 2 x 1 ) + ( ( 4 ↑ 2 ) x 1 ) ) + 3

= ( ( 2 x 1 ) + ( 16 x 1 ) ) + 3

= ( 2 + ( 16 x 1 ) ) + 3

= ( 2 + 16 ) + 3

= 18 + 3

= 21

Problem-03:

Consider the given grammar-

E → E + T / E – T / T

T → T x F / T ÷ F / F

F → F ↑ G / G

G → id

Evaluate the following expression in accordance with the given grammar-

2 ↑ 1 ↑ 4 + 3 x 5 x 6 ↑ 1 + 2 ↑ 3

Solution-

The priority order and associativity of operators on the basis of given grammar is-

id > ↑ > ( x , ÷ ) > ( + , – )

where + , – , x , ÷, ↑ operators are left associative.

Now, we parenthesize the given expression based on the precedence and associativity of operators as-

( ( ( 2 ↑ 1 ) ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )

Now, we evaluate the parenthesized expression as-

= ( ( ( 2 ↑ 1 ) ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )

= ( ( 2 ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )

= ( 16 + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )

= ( 16 + ( ( 3 x 5 ) x 6 ) ) + ( 2 ↑ 3 )

= ( 16 + ( ( 3 x 5 ) x 6 ) ) + 8

= ( 16 + ( 15 x 6 ) ) + 8

= ( 16 + 90 ) + 8

= 106 + 8

= 114

Problem-04:

Consider the given grammar-

E → E ↑ T / T

T → T + F / F

F → G – F / G

G → id

Evaluate the following expression in accordance with the given grammar-

2 ↑ 1 ↑ 3 + 5 – 6 – 8 – 5 + 10 + 11 ↑ 2

Solution-

The priority order and associativity of operators on the basis of given grammar is-

id > – > + > ↑

where-

+ , ↑ operators are left associative.
– is right associative.

Now, we parenthesize the given expression based on the precedence and associativity of operators as-

( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – ( 8 – 5 ) ) ) ) + 10 ) + 11 ) ) ↑ 2

Now, we evaluate the parenthesized expression as-

= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – ( 8 – 5 ) ) ) ) + 10 ) + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – 3 ) ) ) + 10 ) + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – 3 ) ) + 10 ) + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + 2 ) + 10 ) + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ ( ( 5 + 10 ) + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ ( 15 + 11 ) ) ↑ 2

= ( ( 2 ↑ 1 ) ↑ 26 ) ↑ 2

= ( 2 ↑ 26 ) ↑ 2

= (2²⁶) ↑ 2

= (2²⁶)²

Problem-05:

Consider the given priority order of operators-

id > ( x , ÷ ) > ( + , – )

Given all the operators are left associative, construct the corresponding grammar.

Solution-

We apply the rules learnt above in reverse direction to obtain the required grammar.

The corresponding grammar is-

E → E + T / E – T / T

T → T x F / T ÷ F / F

F → id

Problem-06:

Consider the given priority order of operators-

id > ↑ > ( x , ÷ ) > ( + , – )

Given all the operators are left associative, construct the corresponding grammar.

Solution-

The corresponding grammar is-

E → E + T / E – T / T

T → T x F / T ÷ F / F

F → G ↑ F / G

G → id

Next Article- Important Points For Exams

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Chomsky Normal Form | Normal Forms in Automata

Theory of Automata & Computation

Normal Forms-

Normalization is performed in order to standardize the grammar.

By reducing the grammar, the grammar gets minimized but does not gets standardized.
This is because the RHS of productions have no specific format.
In order to standardize the grammar, normalization is performed using normal forms.

Types of Normal Forms-

The most frequently used normal forms are-

Chomsky Normal Form (CNF)
Greibach Normal Form (GNF)

In this article, we will discuss about Chomsky Normal Form.

Chomsky Normal Form-

A context free grammar is said to be in chomsky normal form (CNF) if all its productions are of the form-

A → BC or A → a

where A, B, C are non-terminals and a is a terminal.

From here, we infer-

To be in CNF, all the productions must derive either two non-terminals or a single terminal.
CNF restricts the number of symbols on the right side of a production to be two.
The two symbols must be non-terminals or a single terminal.

Example-

S → AB

A → a

B → b

This context free grammar is in chomsky normal form.

Steps-

The following steps are followed to standardize the grammar using CNF-

Rule-01:

Reduce the grammar completely by-

Eliminating ∈ productions
Eliminating unit productions
Eliminating useless productions

Also Watch- How To Reduce Grammar?

Rule-02:

Replace each production of the form A → B₁B₂B₃….B_n where n > 2 with A → B₁C where C → B₂B₃….B_n.

Repeat this step for all the productions having more than two variables on RHS.

Rule-03:

Replace each production of the form A → aB with A → XB and X → a.

Repeat this step for all the productions having the form A → aB.

PRACTICE PROBLEMS BASED ON CHOMSKY NORMAL FORM-

Problem-01:

Convert the given grammar to CNF-

S → aAD

A → aB / bAB

B → b

D → d

Solution-

Step-01:

The given grammar is already completely reduced.

Step-02:

The productions already in chomsky normal form are-

B → b ………..(1)

D → d ………..(2)

These productions will remain as they are.

The productions not in chomsky normal form are-

S → aAD ………..(3)

A → aB / bAB ………..(4)

We will convert these productions in chomsky normal form.

Step-03:

Replace the terminal symbols a and b by new variables C_a and C_b.

This is done by introducing the following two new productions in the grammar-

C_a → a ………..(5)

C_b → b ………..(6)

Now, the productions (3) and (4) modifies to-

S → C_aAD ………..(7)

A → C_aB / C_bAB ………..(8)

Step-04:

Replace AD and AB by new variables C_AD and C_AB respectively.

This is done by introducing the following two new productions in the grammar-

C_AD → AD ………..(9)

C_AB → AB ………..(10)

Now, the productions (7) and (8) modifies to-

S → C_aC_AD ………..(11)

A → C_aB / C_bC_AB ………..(12)

Step-05:

From (1), (2), (5), (6), (9), (10), (11) and (12), the resultant grammar is-

S → C_aC_AD

A → C_aB / C_bC_AB

B → b

D → d

C_a → a

C_b → b

C_AD → AD

C_AB → AB

This grammar is in chomsky normal form.

Problem-02:

Convert the given grammar to CNF-

S → 1A / 0B

A → 1AA / 0S / 0

B → 0BB / 1S / 1

Solution-

Step-01:

The given grammar is already completely reduced.

Step-02:

The productions already in chomsky normal form are-

A → 0 ………..(1)

B → 1 ………..(2)

These productions will remain as they are.

The productions not in chomsky normal form are-

S → 1A / 0B ………..(3)

A → 1AA / 0S ………..(4)

B → 0BB / 1S ………..(5)

We will convert these productions in chomsky normal form.

Step-03:

Replace the terminal symbols 0 and 1 by new variables C and D.

This is done by introducing the following two new productions in the grammar-

C → 0 ………..(6)

D → 1 ………..(7)

Now, the productions (3), (4) and (5) modifies to-

S → DA / CB ………..(8)

A → DAA / CS ………..(9)

B → CBB / DS ………..(10)

Step-04:

Out of (8), (9) and (10), the productions already in Chomsky Normal Form are-

S → DA / CB ………..(11)

A → CS ………..(12)

B → DS ………..(13)

These productions will remain as they are.

The productions not in chomsky normal form are-

A → DAA ………..(14)

B → CBB ………..(15)

We will convert these productions in Chomsky Normal Form.

Step-05:

Replace AA and BB by new variables E and F respectively.

This is done by introducing the following two new productions in the grammar-

E → AA ………..(16)

F → BB ………..(17)

Now, the productions (14) and (15) modifies to-

A → DE ………..(18)

B → CF ………..(19)

Step-06:

From (1), (2), (6), (7), (11), (12), (13), (16), (17), (18) and (19), the resultant grammar is-

S → DA / CB

A → CS / DE / 0

B → DS / CF / 1

C → 0

D → 1

E → AA

F → BB

This grammar is in chomsky normal form.

To gain better understanding about Chomsky Normal Form,

Watch this Video Lecture

Next Article- Algorithm To Decide Whether CFL Is Empty

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Minimization of DFA | Minimize DFA | Examples

Theory of Automata & Computation

Minimization of DFA-

The process of reducing a given DFA to its minimal form is called as minimization of DFA.

It contains the minimum number of states.
The DFA in its minimal form is called as a Minimal DFA.

How To Minimize DFA?

The two popular methods for minimizing a DFA are-

In this article, we will discuss Minimization of DFA Using Equivalence Theorem.

Minimization of DFA Using Equivalence Theorem-

Step-01:

Eliminate all the dead states and inaccessible states from the given DFA (if any).

Dead State

All those non-final states which transit to itself for all input symbols in ∑ are called as dead states.

Inaccessible State

All those states which can never be reached from the initial state are called as inaccessible states.

Step-02:

Draw a state transition table for the given DFA.
Transition table shows the transition of all states on all input symbols in Σ.

Step-03:

Now, start applying equivalence theorem.

Take a counter variable k and initialize it with value 0.
Divide Q (set of states) into two sets such that one set contains all the non-final states and other set contains all the final states.
This partition is called P₀.

Step-04:

Increment k by 1.
Find P_k by partitioning the different sets of P_k-1 .
In each set of P_k-1 , consider all the possible pair of states within each set and if the two states are distinguishable, partition the set into different sets in P_k.

Two states q₁ and q₂ are distinguishable in partition P_k for any input symbol ‘a’,

if δ (q₁, a) and δ (q₂, a) are in different sets in partition P_k-1.

Step-05:

Repeat step-04 until no change in partition occurs.
In other words, when you find P_k = P_k-1, stop.

Step-06:

All those states which belong to the same set are equivalent.
The equivalent states are merged to form a single state in the minimal DFA.

Number of states in Minimal DFA

= Number of sets in P_k

PRACTICE PROBLEMS BASED ON MINIMIZATION OF DFA-

Problem-01:

Minimize the given DFA-

Solution-

Step-01:

The given DFA contains no dead states and inaccessible states.

Step-02:

Draw a state transition table-

	a	b
→q0	q1	q2
q1	q1	q3
q2	q1	q2
q3	q1	*q4
*q4	q1	q2

Step-03:

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ , q₃ } { q₄ }

P₁ = { q₀ , q₁ , q₂ } { q₃ } { q₄ }

P₂ = { q₀ , q₂ } { q₁ } { q₃ } { q₄ }

P₃ = { q₀ , q₂ } { q₁ } { q₃ } { q₄ }

Since P₃ = P₂, so we stop.

From P₃, we infer that states q₀ and q₂ are equivalent and can be merged together.

So, Our minimal DFA is-

Problem-02:

Minimize the given DFA-

Solution-

Step-01:

State q₃ is inaccessible from the initial state.
So, we eliminate it and its associated edges from the DFA.

The resulting DFA is-

Step-02:

Draw a state transition table-

	a	b
→q0	*q1	q0
*q1	*q2	*q1
*q2	*q1	*q2

Step-03:

Now using Equivalence Theorem, we have-

P₀ = { q₀ } { q₁ , q₂ }

P₁ = { q₀ } { q₁ , q₂ }

Since P₁ = P₀, so we stop.

From P₁, we infer that states q₁ and q₂ are equivalent and can be merged together.

So, Our minimal DFA is-

Problem-03:

Minimize the given DFA-

Solution-

Step-01:

The given DFA contains no dead states and inaccessible states.

Step-02:

Draw a state transition table-

	0	1
→q0	q1	q3
q1	q2	*q4
q2	q1	*q4
q3	q2	*q4
*q4	*q4	*q4

Step-03:

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ , q₃ } { q₄ }

P₁ = { q₀ } { q₁ , q₂ , q₃ } { q₄ }

P₂ = { q₀ } { q₁ , q₂ , q₃ } { q₄ }

Since P₂ = P₁, so we stop.

From P₂, we infer that states q₁ , q₂ and q₃ are equivalent and can be merged together.

So, Our minimal DFA is-

Problem-04:

Minimize the given DFA-

Solution-

Step-01:

State q₅ is inaccessible from the initial state.
So, we eliminate it and its associated edges from the DFA.

The resulting DFA is-

Step-02:

Draw a state transition table-

	0	1
→q0	q1	q2
q1	q2	*q3
q2	q2	*q4
*q3	*q3	*q3
*q4	*q4	*q4

Step-03:

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ } { q₃ , q₄ }

P₁ = { q₀ } { q₁ , q₂ } { q₃ , q₄ }

P₂ = { q₀ } { q₁ , q₂ } { q₃ , q₄ }

Since P₂ = P₁, so we stop.

From P₂, we infer-

States q₁ and q₂ are equivalent and can be merged together.
States q₃ and q₄ are equivalent and can be merged together.

So, Our minimal DFA is-

Also Read- Construction of DFA

To gain better understanding about Minimization of DFA,

Watch this Video Lecture

Next Article- Converting DFA to Regular Expression

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

DFA to Regular Expression | Examples

Theory of Automata & Computation

DFA to Regular Expression-

The two popular methods for converting a DFA to its regular expression are-

Arden’s Method
State Elimination Method

In this article, we will discuss State Elimination Method.

State Elimination Method-

This method involves the following steps in finding the regular expression for any given DFA-

Step-01:

Thumb Rule

The initial state of the DFA must not have any incoming edge.

If there exists any incoming edge to the initial state, then create a new initial state having no incoming edge to it.

Example-

Step-02:

Thumb Rule

There must exist only one final state in the DFA.

If there exists multiple final states in the DFA, then convert all the final states into non-final states and create a new single final state.

Example-

Step-03:

Thumb Rule

The final state of the DFA must not have any outgoing edge.

If there exists any outgoing edge from the final state, then create a new final state having no outgoing edge from it.

Example-

Step-04:

Eliminate all the intermediate states one by one.
These states may be eliminated in any order.

In the end,

Only an initial state going to the final state will be left.
The cost of this transition is the required regular expression.

NOTE

The state elimination method can be applied to any finite automata.

(NFA, ∈-NFA, DFA etc)

Also Read- Construction of DFA

PRACTICE PROBLEMS BASED ON CONVERTING DFA TO REGULAR EXPRESSION-

Problem-01:

Find regular expression for the following DFA-

Solution-

Step-01:

Initial state A has an incoming edge.
So, we create a new initial state q_i.

The resulting DFA is-

Step-02:

Final state B has an outgoing edge.
So, we create a new final state q_f^.

The resulting DFA is-

Step-03:

Now, we start eliminating the intermediate states.

First, let us eliminate state A.

There is a path going from state q_i to state B via state A.
So, after eliminating state A, we put a direct path from state q_i to state B having cost ∈.0 = 0
There is a loop on state B using state A.
So, after eliminating state A, we put a direct loop on state B having cost 1.0 = 10.

Eliminating state A, we get-

Step-04:

Now, let us eliminate state B.

There is a path going from state q_i to state q_f via state B.
So, after eliminating state B, we put a direct path from state q_i to state q_f having cost 0.(10)*.∈ = 0(10)*

Eliminating state B, we get-

From here,

Regular Expression = 0(10)*

NOTE-

In the above question,

If we first eliminate state B and then state A, then regular expression would be = (01)*0.
This is also the same and correct.

Problem-02:

Find regular expression for the following DFA-

Solution-

Step-01:

There exist multiple final states.
So, we convert them into a single final state.

The resulting DFA is-

Step-02:

Now, we start eliminating the intermediate states.

First, let us eliminate state q₄.

There is a path going from state q₂ to state q_f via state q₄.
So, after eliminating state q₄ , we put a direct path from state q₂ to state q_f having cost b.∈ = b.

Step-03:

Now, let us eliminate state q₃.

There is a path going from state q₂ to state q_f via state q₃.
So, after eliminating state q₃ , we put a direct path from state q₂ to state q_f having cost c.∈ = c.

Step-04:

Now, let us eliminate state q₅.

There is a path going from state q₂ to state q_f via state q₅.
So, after eliminating state q₅ , we put a direct path from state q₂ to state q_f having cost d.∈ = d.

Step-05:

Now, let us eliminate state q₂.

There is a path going from state q₁ to state q_f via state q₂.
So, after eliminating state q₂ , we put a direct path from state q₁ to state q_f having cost a.(b+c+d).

From here,

Regular Expression = a(b+c+d)

Problem-03:

Find regular expression for the following DFA-

Solution-

Step-01:

Initial state q₁ has an incoming edge.
So, we create a new initial state q_i.

The resulting DFA is-

Step-02:

Final state q₂ has an outgoing edge.
So, we create a new final state q_f.

The resulting DFA is-

Step-03:

Now, we start eliminating the intermediate states.

First, let us eliminate state q₁.

There is a path going from state q_i to state q₂ via state q₁ .
So, after eliminating state q₁, we put a direct path from state q_i to state q₂ having cost ∈.c*.a = c*a
There is a loop on state q₂ using state q₁ .
So, after eliminating state q₁ , we put a direct loop on state q₂ having cost b.c*.a = bc*a

Eliminating state q₁, we get-

Step-04:

Now, let us eliminate state q₂.

There is a path going from state q_i to state q_f via state q₂ .
So, after eliminating state q₂, we put a direct path from state q_i to state q_f having cost c*a(d+bc*a)*∈ = c*a(d+bc*a)*

Eliminating state q₂, we get-

From here,

Regular Expression = c*a(d+bc*a)*

Problem-04:

Find regular expression for the following DFA-

Solution-

Step-01:

State D is a dead state as it does not reach to any final state.
So, we eliminate state D and its associated edges.

The resulting DFA is-

Step-02:

Initial state A has an incoming edge (self loop).
So, we create a new initial state q_i.

The resulting DFA is-

Step-03:

There exist multiple final states.
So, we convert them into a single final state.

The resulting DFA is-

Step-04:

Now, we start eliminating the intermediate states.

First, let us eliminate state C.

There is a path going from state B to state q_f via state C.
So, after eliminating state C, we put a direct path from state B to state q_f having cost b.b*.∈ = bb*

Eliminating state C, we get-

Step-05:

Now, let us eliminate state B.

There is a path going from state A to state q_f via state B.
So, after eliminating state B, we put a direct path from state A to state q_f having cost a.a*.(bb*+∈) = aa*(bb*+∈)

Eliminating state B, we get-

Step-06:

Now, let us eliminate state A.

There is a path going from state q_i to state q_f via state A.
So, after eliminating state A, we put a direct path from state q_i to state q_f having cost ∈.b*.(aa*(bb*+∈)+∈) = b*(aa*(bb*+∈)+∈)

Eliminating state A, we get-

From here,

Regular Expression = b*(aa*(bb*+∈)+∈)

We know, bb* + ∈ = b*

So, we can also write-

Regular Expression = b*(aa*b*+∈)

Problem-05:

Find regular expression for the following DFA-

Solution-

Step-01:

Since initial state A has an incoming edge, so we create a new initial state q_i.
Since final state A has an outgoing edge, so we create a new final state q_f.

The resulting DFA is-

Step-02:

Now, we start eliminating the intermediate states.

First, let us eliminate state B.

There is a path going from state C to state A via state B.
So, after eliminating state B, we put a direct path from state C to state A having cost b.b = bb.
There is a loop on state A using state B.
So, after eliminating state B, we put a direct loop on state A having cost a.b = ab.

Eliminating state B, we get-

Step-03:

Now, let us eliminate state C.

There is a loop on state A using state C.
So, after eliminating state C, we put a direct loop on state A having cost b.(a+bb) = b(a+bb)

Eliminating state C, we get-

Step-04:

Now, let us eliminate state A.

There is a path going from state q_i to state q_f via state A.
So, after eliminating state A, we put a direct path from state q_i to state q_f having cost ∈.(ab + b(a+bb))*∈ = (ab + b(a+bb))*

Eliminating state A, we get-

From here,

Regular Expression = (ab + b(a+bb))*

Problem-06:

Find regular expression for the following DFA-

Solution-

State B is a dead state as it does not reach to the final state.
So, we eliminate state B and its associated edges.

The resulting DFA is-

From here,

Regular Expression = a

Problem-07:

Find regular expression for the following DFA-

Solution-

Step-01:

There exist multiple final states.
So, we create a new single final state.

The resulting DFA is-

Step-02:

Now, we start eliminating the intermediate states.

First, let us eliminate state B.

There is a path going from state A to state q_f via state B.
So, after eliminating state B, we put a direct path from state A to state q_f having cost a.a*.∈ = aa*.

Eliminating state B, we get-

Step-03:

Now, let us eliminate state C.

There is a path going from state A to state q_f via state C.
So, after eliminating state C, we put a direct path from state A to state q_f having cost b.a*.∈ = ba*.

Eliminating state C, we get-

From here,

Regular Expression = aa* + ba*

Also Read- Minimization of DFA

To gain better understanding about Converting DFA to Regular Expression,

Watch this Video Lecture

Next Article- Arden’s Theorem

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Left Recursion | Left Recursion Elimination

Theory of Automata & Computation

Recursion-

Recursion can be classified into following three types-

Left Recursion
Right Recursion
General Recursion

1. Left Recursion-

A production of grammar is said to have left recursion if the leftmost variable of its RHS is same as variable of its LHS.
A grammar containing a production having left recursion is called as Left Recursive Grammar.

Example-

S → Sa / ∈

(Left Recursive Grammar)

Left recursion is considered to be a problematic situation for Top down parsers.
Therefore, left recursion has to be eliminated from the grammar.

Elimination of Left Recursion

Left recursion is eliminated by converting the grammar into a right recursive grammar.

If we have the left-recursive pair of productions-

A → Aα / β

(Left Recursive Grammar)

where β does not begin with an A.

Then, we can eliminate left recursion by replacing the pair of productions with-

A → βA’

A’ → αA’ / ∈

(Right Recursive Grammar)

This right recursive grammar functions same as left recursive grammar.

2. Right Recursion-

A production of grammar is said to have right recursion if the rightmost variable of its RHS is same as variable of its LHS.
A grammar containing a production having right recursion is called as Right Recursive Grammar.

Example-

S → aS / ∈

(Right Recursive Grammar)

Right recursion does not create any problem for the Top down parsers.
Therefore, there is no need of eliminating right recursion from the grammar.

Also Read- Types of Recursive Grammar

3. General Recursion-

The recursion which is neither left recursion nor right recursion is called as general recursion.

Example-

S → aSb / ∈

PRACTICE PROBLEMS BASED ON LEFT RECURSION ELIMINATION-

Problem-01:

Consider the following grammar and eliminate left recursion-

A → ABd / Aa / a

B → Be / b

Solution-

The grammar after eliminating left recursion is-

A → aA’

A’ → BdA’ / aA’ / ∈

B → bB’

B’ → eB’ / ∈

Problem-02:

Consider the following grammar and eliminate left recursion-

E → E + E / E x E / a

Solution-

The grammar after eliminating left recursion is-

E → aA

A → +EA / xEA / ∈

Problem-03:

Consider the following grammar and eliminate left recursion-

E → E + T / T

T → T x F / F

F → id

Solution-

The grammar after eliminating left recursion is-

E → TE’

E’ → +TE’ / ∈

T → FT’

T’ → xFT’ / ∈

F → id

Problem-04:

Consider the following grammar and eliminate left recursion-

S → (L) / a

L → L , S / S

Solution-

The grammar after eliminating left recursion is-

S → (L) / a

L → SL’

L’ → ,SL’ / ∈

Problem-05:

Consider the following grammar and eliminate left recursion-

S → S0S1S / 01

Solution-

The grammar after eliminating left recursion is-

S → 01A

A → 0S1SA / ∈

Problem-06:

Consider the following grammar and eliminate left recursion-

S → A

A → Ad / Ae / aB / ac

B → bBc / f

Solution-

The grammar after eliminating left recursion is-

S → A

A → aBA’ / acA’

A’ → dA’ / eA’ / ∈

B → bBc / f

Problem-07:

Consider the following grammar and eliminate left recursion-

A → AAα / β

Solution-

The grammar after eliminating left recursion is-

A → βA’

A’ → AαA’ / ∈

Problem-08:

Consider the following grammar and eliminate left recursion-

A → Ba / Aa / c

B → Bb / Ab / d

Solution-

This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from A → Ba / Aa / c

Eliminating left recursion from here, we get-

A → BaA’ / cA’

A’ → aA’ / ∈

Now, given grammar becomes-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / Ab / d

Step-02:

Substituting the productions of A in B → Ab, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / BaA’b / cA’b / d

Step-03:

Now, eliminating left recursion from the productions of B, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → cA’bB’ / dB’

B’ → bB’ / aA’bB’ / ∈

This is the final grammar after eliminating left recursion.

Problem-09:

Consider the following grammar and eliminate left recursion-

X → XSb / Sa / b

S → Sb / Xa / a

Solution-

This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from X → XSb / Sa / b

Eliminating left recursion from here, we get-

X → SaX’ / bX’

X’ → SbX’ / ∈

Now, given grammar becomes-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / Xa / a

Step-02:

Substituting the productions of X in S → Xa, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / SaX’a / bX’a / a

Step-03:

Now, eliminating left recursion from the productions of S, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → bX’aS’ / aS’

S’ → bS’ / aX’aS’ / ∈

This is the final grammar after eliminating left recursion.

Problem-10:

Consider the following grammar and eliminate left recursion-

S → Aa / b

A → Ac / Sd / ∈

Solution-

This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from S → Aa / b

This is already free from left recursion.

Step-02:

Substituting the productions of S in A → Sd, we get the following grammar-

S → Aa / b

A → Ac / Aad / bd / ∈

Step-03:

Now, eliminating left recursion from the productions of A, we get the following grammar-

S → Aa / b

A → bdA’ / A’

A’ → cA’ / adA’ / ∈

This is the final grammar after eliminating left recursion.

Also Read- Left Factoring

To gain better understanding about Left Recursion Elimination,

Watch this Video Lecture

Next Article- Types of Grammars

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

← Older Posts

Newer Posts →