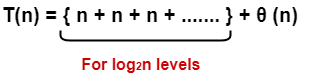Searching-
- Searching is a process of finding a particular element among several given elements.
- The search is successful if the required element is found.
- Otherwise, the search is unsuccessful.
Searching Algorithms-
Searching Algorithms are a family of algorithms used for the purpose of searching.
The searching of an element in the given array may be carried out in the following two ways-

- Linear Search
- Binary Search
In this article, we will discuss about Binary Search Algorithm.
Binary Search-
- Binary Search is one of the fastest searching algorithms.
- It is used for finding the location of an element in a linear array.
- It works on the principle of divide and conquer technique.
Binary Search Algorithm can be applied only on Sorted arrays.
So, the elements must be arranged in-
- Either ascending order if the elements are numbers.
- Or dictionary order if the elements are strings.
To apply binary search on an unsorted array,
- First, sort the array using some sorting technique.
- Then, use binary search algorithm.
Also Read- Linear Search
Binary Search Algorithm-
Consider-
- There is a linear array ‘a’ of size ‘n’.
- Binary search algorithm is being used to search an element ‘item’ in this linear array.
- If search ends in success, it sets loc to the index of the element otherwise it sets loc to -1.
- Variables beg and end keeps track of the index of the first and last element of the array or sub array in which the element is being searched at that instant.
- Variable mid keeps track of the index of the middle element of that array or sub array in which the element is being searched at that instant.
Then, Binary Search Algorithm is as follows-
Begin
Set beg = 0
Set end = n-1
Set mid = (beg + end) / 2
while ( (beg <= end) and (a[mid] ≠ item) ) do
if (item < a[mid]) then
Set end = mid - 1
else
Set beg = mid + 1
endif
Set mid = (beg + end) / 2
endwhile
if (beg > end) then
Set loc = -1
else
Set loc = mid
endif
End
Explanation
Binary Search Algorithm searches an element by comparing it with the middle most element of the array. Then, following three cases are possible-
Case-01
If the element being searched is found to be the middle most element, its index is returned.
Case-02
If the element being searched is found to be greater than the middle most element, then its search is further continued in the right sub array of the middle most element.
Case-03
If the element being searched is found to be smaller than the middle most element, then its search is further continued in the left sub array of the middle most element.
This iteration keeps on repeating on the sub arrays until the desired element is found or size of the sub array reduces to zero. |
Time Complexity Analysis-
Binary Search time complexity analysis is done below-
- In each iteration or in each recursive call, the search gets reduced to half of the array.
- So for n elements in the array, there are log2n iterations or recursive calls.
Thus, we have-
| Time Complexity of Binary Search Algorithm is O(log2n).
Here, n is the number of elements in the sorted linear array. |
This time complexity of binary search remains unchanged irrespective of the element position even if it is not present in the array.
Binary Search Example-
Consider-
- We are given the following sorted linear array.
- Element 15 has to be searched in it using Binary Search Algorithm.

Binary Search Algorithm works in the following steps-
Step-01:
- To begin with, we take beg=0 and end=6.
- We compute location of the middle element as-
mid
= (beg + end) / 2
= (0 + 6) / 2
= 3
- Here, a[mid] = a[3] = 20 ≠ 15 and beg < end.
- So, we start next iteration.
Step-02:
- Since a[mid] = 20 > 15, so we take end = mid – 1 = 3 – 1 = 2 whereas beg remains unchanged.
- We compute location of the middle element as-
mid
= (beg + end) / 2
= (0 + 2) / 2
= 1
- Here, a[mid] = a[1] = 10 ≠ 15 and beg < end.
- So, we start next iteration.
Step-03:
- Since a[mid] = 10 < 15, so we take beg = mid + 1 = 1 + 1 = 2 whereas end remains unchanged.
- We compute location of the middle element as-
mid
= (beg + end) / 2
= (2 + 2) / 2
= 2
- Here, a[mid] = a[2] = 15 which matches to the element being searched.
- So, our search terminates in success and index 2 is returned.
Binary Search Algorithm Advantages-
The advantages of binary search algorithm are-
- It eliminates half of the list from further searching by using the result of each comparison.
- It indicates whether the element being searched is before or after the current position in the list.
- This information is used to narrow the search.
- For large lists of data, it works significantly better than linear search.
Binary Search Algorithm Disadvantages-
The disadvantages of binary search algorithm are-
- It employs recursive approach which requires more stack space.
- Programming binary search algorithm is error prone and difficult.
- The interaction of binary search with memory hierarchy i.e. caching is poor.
(because of its random access nature)
Important Note-
For in-memory searching, if the interval to be searched is small,
- Linear search may exhibit better performance than binary search.
- This is because it exhibits better locality of reference.
To gain better understanding about Binary Search Algorithm,
Next Article- Selection Sort
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.