Category: Database Management System

Determine Decomposition Is Lossless Or Lossy

Database Management System

Decomposition in DBMS-

 

Before you go through this article, make sure that you have gone through the previous article on Decomposition in DBMS.

 

We have discussed-

  • Decomposition is a process of dividing a single relation into two or more sub relations.
  • Decomposition of a relation can be completed in the following two ways-

 

 

  1. Lossless Join Decomposition
  2. Lossy Join Decomposition

 

In this article, we will learn how to determine whether the decomposition is lossless or lossy.

 

Determining Whether Decomposition Is Lossless Or Lossy-

 

Consider a relation R is decomposed into two sub relations R1 and R2.

Then,

  • If all the following conditions satisfy, then the decomposition is lossless.
  • If any of these conditions fail, then the decomposition is lossy.

 

Condition-01:

 

Union of both the sub relations must contain all the attributes that are present in the original relation R.

Thus,

R1 ∪ R2 = R

 

Condition-02:

 

  • Intersection of both the sub relations must not be null.
  • In other words, there must be some common attribute which is present in both the sub relations.

Thus,

R1 ∩ R2 ≠ ∅

 

Condition-03:

 

Intersection of both the sub relations must be a super key of either R1 or R2 or both.

Thus,

R1 ∩ R2 = Super key of R1 or R2

 

PRACTICE PROBLEMS BASED ON DETERMINING WHETHER DECOMPOSITION IS LOSSLESS OR LOSSY-

 

Problem-01:

 

Consider a relation schema R ( A , B , C , D ) with the functional dependencies A → B and C → D. Determine whether the decomposition of R into R1 ( A , B ) and R2 ( C , D ) is lossless or lossy.

 

Solution-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R.

So, we have-

 R1 ( A , B ) ∪ R2 ( C , D )

= R ( A , B , C , D )

Clearly, union of the sub relations contain all the attributes of relation R.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

R1 ( A , B ) ∩ R2 ( C , D )

= Φ

Clearly, intersection of the sub relations is null.

So, condition-02 fails.

Thus, we conclude that the decomposition is lossy.

 

Problem-02:

 

Consider a relation schema R ( A , B , C , D ) with the following functional dependencies-

A → B

B → C

C → D

D → B

Determine whether the decomposition of R into R1 ( A , B ) , R2 ( B , C ) and R3 ( B , D ) is lossless or lossy.

 

Solution-

 

Strategy to Solve

 

When a given relation is decomposed into more than two sub relations, then-

  • Consider any one possible ways in which the relation might have been decomposed into those sub relations.
  • First, divide the given relation into two sub relations.
  • Then, divide the sub relations according to the sub relations given in the question.

As a thumb rule, remember-

Any relation can be decomposed only into two sub relations at a time.

 

Consider the original relation R was decomposed into the given sub relations as shown-

 

 

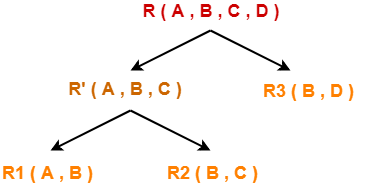
Decomposition of R(A, B, C, D) into R'(A, B, C) and R3(B, D)-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R.

So, we have-

 R‘ ( A , B , C ) ∪ R3 ( B , D )

= R ( A , B , C , D )

Clearly, union of the sub relations contain all the attributes of relation R.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

 R‘ ( A , B , C ) ∩ R3 ( B , D )

= B

Clearly, intersection of the sub relations is not null.

Thus, condition-02 satisfies.

 

Condition-03:

 

According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.

So, we have-

 R‘ ( A , B , C ) ∩ R3 ( B , D )

= B

Now, the closure of attribute B is-

B+ = { B , C , D }

Now, we see-

  • Attribute ‘B’ can not determine attribute ‘A’ of sub relation R’.
  • Thus, it is not a super key of the sub relation R’.
  • Attribute ‘B’ can determine all the attributes of sub relation R3.
  • Thus, it is a super key of the sub relation R3.

 

Clearly, intersection of the sub relations is a super key of one of the sub relations.

So, condition-03 satisfies.

Thus, we conclude that the decomposition is lossless.

 

Decomposition of R'(A, B, C) into R1(A, B) and R2(B, C)-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R’.

So, we have-

 R1 ( A , B ) ∪ R2 ( B , C )

= R’ ( A , B , C )

Clearly, union of the sub relations contain all the attributes of relation R’.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

 R1 ( A , B ) ∩ R2 ( B , C )

= B

Clearly, intersection of the sub relations is not null.

Thus, condition-02 satisfies.

 

Condition-03:

 

According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.

So, we have-

 R1 ( A , B ) ∩ R2 ( B , C )

= B

Now, the closure of attribute B is-

B+ = { B , C , D }

Now, we see-

  • Attribute ‘B’ can not determine attribute ‘A’ of sub relation R1.
  • Thus, it is not a super key of the sub relation R1.
  • Attribute ‘B’ can determine all the attributes of sub relation R2.
  • Thus, it is a super key of the sub relation R2.

 

Clearly, intersection of the sub relations is a super key of one of the sub relations.

So, condition-03 satisfies.

Thus, we conclude that the decomposition is lossless.

 

Conclusion-

Overall decomposition of relation R into sub relations R1, R2 and R3 is lossless.

 

Next Article- Introduction to Normal Forms

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Closure in DBMS | Steps to Find Closure

Database Management System

Closure of an Attribute Set-

 

  • The set of all those attributes which can be functionally determined from an attribute set is called as a closure of that attribute set.
  • Closure of attribute set {X} is denoted as {X}+.

 

Steps to Find Closure of an Attribute Set-

 

Following steps are followed to find the closure of an attribute set-

 

Step-01:

 

Add the attributes contained in the attribute set for which closure is being calculated to the result set.

 

Step-02:

 

Recursively add the attributes to the result set which can be functionally determined from the attributes already contained in the result set.

 

Example-

 

Consider a relation R ( A , B , C , D , E , F , G ) with the functional dependencies-

A → BC

BC → DE

D → F

CF → G

 

Now, let us find the closure of some attributes and attribute sets-

 

Closure of attribute A-

 

A+   = { A }

= { A , B , C }                          ( Using A → BC )

= { A , B , C , D , E }               ( Using BC → DE )

= { A , B , C , D , E , F }          ( Using D → F )

= { A , B , C , D , E , F , G }    ( Using CF → G )

Thus,

A+ = { A , B , C , D , E , F , G }

 

Closure of attribute D-

 

D+   = { D }

= { D , F }   ( Using D → F )

We can not determine any other attribute using attributes D and F contained in the result set.

Thus,

D+ = { D , F }

 

Closure of attribute set {B, C}-

 

{ B , C }+= { B , C }

= { B , C , D , E }               ( Using BC → DE )

= { B , C , D , E , F }          ( Using D → F )

= { B , C , D , E , F , G }    ( Using CF → G )

Thus,

{ B , C }+ = { B , C , D , E , F , G }

 

Finding the Keys Using Closure-

 

Super Key-

 

  • If the closure result of an attribute set contains all the attributes of the relation, then that attribute set is called as a super key of that relation.
  • Thus, we can say-

“The closure of a super key is the entire relation schema.”

 

Example-

 

In the above example,

  • The closure of attribute A is the entire relation schema.
  • Thus, attribute A is a super key for that relation.

 

Candidate Key-

 

  • If there exists no subset of an attribute set whose closure contains all the attributes of the relation, then that attribute set is called as a candidate key of that relation.

 

Example-

 

In the above example,

  • No subset of attribute A contains all the attributes of the relation.
  • Thus, attribute A is also a candidate key for that relation.

 

Also Read- How To Find Candidate Keys?

 

PRACTICE PROBLEM BASED ON FINDING CLOSURE OF AN ATTRIBUTE SET-

 

Problem-

 

Consider the given functional dependencies-

AB → CD

AF → D

DE → F

C → G

F → E

G → A

 

Which of the following options is false?

(A) { CF }+ = { A , C , D , E , F , G }

(B) { BG }+ = { A , B , C , D , G }

(C) { AF }+ = { A , C , D , E , F , G }

(D) { AB }+ = { A , C , D , F ,G }

 

Solution-

 

Let us check each option one by one-

 

Option-(A):

 

{ CF }+  = { C , F }

      = { C , F , G }                     ( Using C → G )

      = { C , E , F , G }               ( Using F → E )

      = { A , C , E , E , F }          ( Using G → A )

      = { A , C , D , E , F , G }    ( Using AF → D )

 

Since, our obtained result set is same as the given result set, so, it means it is correctly given.

 

Option-(B):

 

{ BG }+  = { B , G }

      = { A , B , G }                   ( Using G → A )

      = { A , B , C , D , G }        ( Using AB → CD )

 

Since, our obtained result set is same as the given result set, so, it means it is correctly given.

 

Option-(C):

 

{ AF }+  = { A , F }

      = { A , D , F }               ( Using AF → D )

      = { A , D , E , F }          ( Using F → E )

 

Since, our obtained result set is different from the given result set, so,it means it is not correctly given.

 

Option-(D):

 

{ AB }+  = { A , B }

      = { A , B , C , D }            ( Using AB → CD )

      = { A , B , C , D , G }      ( Using C → G )

 

Since, our obtained result set is different from the given result set, so,it means it is not correctly given.

Thus,

Option (C) and Option (D) are correct.

 

Next Article- 10 Different Kinds of Keys in DBMS

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Decomposition in DBMS | Lossless | Lossy

Database Management System

Decomposition of a Relation-

 

The process of breaking up or dividing a single relation into two or more sub relations is called as decomposition of a relation.

 

Properties of Decomposition-

 

The following two properties must be followed when decomposing a given relation-

 

1. Lossless decomposition-

 

Lossless decomposition ensures-

  • No information is lost from the original relation during decomposition.
  • When the sub relations are joined back, the same relation is obtained that was decomposed.

Every decomposition must always be lossless.

 

2. Dependency Preservation-

 

Dependency preservation ensures-

  • None of the functional dependencies that holds on the original relation are lost.
  • The sub relations still hold or satisfy the functional dependencies of the original relation.

 

Types of Decomposition-

 

Decomposition of a relation can be completed in the following two ways-

 

 

1. Lossless Join Decomposition-

 

  • Consider there is a relation R which is decomposed into sub relations R1 , R2 , …. , Rn.
  • This decomposition is called lossless join decomposition when the join of the sub relations results in the same relation R that was decomposed.
  • For lossless join decomposition, we always have-

 

R1 ⋈ R2 ⋈ R3 ……. ⋈ Rn = R 

where ⋈ is a natural join operator

 

Example-

 

Consider the following relation R( A , B , C )-

 

A B C
1 2 1
2 5 3
3 3 3

R( A , B , C )

 

Consider this relation is decomposed into two sub relations R1( A , B ) and R2( B , C )-

 

 

The two sub relations are-

 

A B
1 2
2 5
3 3

R1( A , B )

 

B C
2 1
5 3
3 3

R2( B , C )

 

Now, let us check whether this decomposition is lossless or not.

For lossless decomposition, we must have-

R1 ⋈ R2 = R

 

Now, if we perform the natural join ( ⋈ ) of the sub relations R1 and R2 , we get-

 

A B C
1 2 1
2 5 3
3 3 3

 

This relation is same as the original relation R.

Thus, we conclude that the above decomposition is lossless join decomposition.

 

NOTE-

 

  • Lossless join decomposition is also known as non-additive join decomposition.
  • This is because the resultant relation after joining the sub relations is same as the decomposed relation.
  • No extraneous tuples appear after joining of the sub-relations.

 

2. Lossy Join Decomposition-

 

  • Consider there is a relation R which is decomposed into sub relations R1 , R2 , …. , Rn.
  • This decomposition is called lossy join decomposition when the join of the sub relations does not result in the same relation R that was decomposed.
  • The natural join of the sub relations is always found to have some extraneous tuples.
  • For lossy join decomposition, we always have-

 

R1 ⋈ R2 ⋈ R3 ……. ⋈ Rn ⊃ R 

where ⋈ is a natural join operator

 

Example-

 

Consider the following relation R( A , B , C )-

 

A B C
1 2 1
2 5 3
3 3 3

R( A , B , C )

 

Consider this relation is decomposed into two sub relations as R1( A , C ) and R2( B , C )-

 

 

The two sub relations are-

 

A C
1 1
2 3
3 3

R1( A , B )

 

B C
2 1
5 3
3 3

R2( B , C )

 

Now, let us check whether this decomposition is lossy or not.

For lossy decomposition, we must have-

R1 ⋈ R2 ⊃ R

 

Now, if we perform the natural join ( ⋈ ) of the sub relations R1 and R2 we get-

 

A B C
1 2 1
2 5 3
2 3 3
3 5 3
3 3 3

 

This relation is not same as the original relation R and contains some extraneous tuples.

Clearly, R1 ⋈ R2 ⊃ R.

Thus, we conclude that the above decomposition is lossy join decomposition.

 

NOTE-

 

  • Lossy join decomposition is also known as careless decomposition.
  • This is because extraneous tuples get introduced in the natural join of the sub-relations.
  • Extraneous tuples make the identification of the original tuples difficult.

 

Next Article- Rules to Determine Lossless and Lossy Decomposition

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Equivalence of Two Sets of Functional Dependencies

Database Management System

Equivalence of Two Sets of Functional Dependencies-

 

Before you go through this article, make sure that you have gone through the previous article on Functional Dependency.

 

In DBMS,

  • Two different sets of functional dependencies for a given relation may or may not be equivalent.
  • If F and G are the two sets of functional dependencies, then following 3 cases are possible-

 

Case-01: F covers G (F ⊇ G)

Case-02: G covers F (G ⊇ F)

Case-03: Both F and G cover each other (F = G)

 

Case-01: Determining Whether F Covers G-

 

Following steps are followed to determine whether F covers G or not-

 

Step-01:

 

  • Take the functional dependencies of set G into consideration.
  • For each functional dependency X → Y, find the closure of X using the functional dependencies of set G.

 

Step-02:

 

  • Take the functional dependencies of set G into consideration.
  • For each functional dependency X → Y, find the closure of X using the functional dependencies of set F.

 

Step-03:

 

  • Compare the results of Step-01 and Step-02.
  • If the functional dependencies of set F has determined all those attributes that were determined by the functional dependencies of set G, then it means F covers G.
  • Thus, we conclude F covers G (F ⊇ G) otherwise not.

 

Case-02: Determining Whether G Covers F-

 

Following steps are followed to determine whether G covers F or not-

 

Step-01:

 

  • Take the functional dependencies of set F into consideration.
  • For each functional dependency X → Y, find the closure of X using the functional dependencies of set F.

 

Step-02:

 

  • Take the functional dependencies of set F into consideration.
  • For each functional dependency X → Y, find the closure of X using the functional dependencies of set G.

 

Step-03:

 

  • Compare the results of Step-01 and Step-02.
  • If the functional dependencies of set G has determined all those attributes that were determined by the functional dependencies of set F, then it means G covers F.
  • Thus, we conclude G covers F (G ⊇ F) otherwise not.

 

Case-03: Determining Whether Both F and G Cover Each Other-

 

  • If F covers G and G covers F, then both F and G cover each other.
  • Thus, if both the above cases hold true, we conclude both F and G cover each other (F = G).

 

PRACTICE PROBLEM BASED ON EQUIVALENCE OF FUNCTIONAL DEPENDENCIES-

 

Problem-

 

A relation R (A , C , D , E , H) is having two functional dependencies sets F and G as shown-

 

Set F-

A → C

AC → D

E → AD

E → H

 

Set G-

A → CD

E → AH

 

Which of the following holds true?

(A) G ⊇ F

(B) F ⊇ G

(C) F = G

(D) All of the above

 

Solution-

 

Determining whether F covers G-

 

Step-01:

 

  • (A)+ = { A , C , D }               // closure of left side of A → CD using set G
  • (E)+ = { A , C , D , E , H }    // closure of left side of E → AH using set G

 

Step-02:

 

  • (A)+ = { A , C , D }               // closure of left side of A → CD using set F
  • (E)+ = { A , C , D , E , H }    // closure of left side of E → AH using set F

 

Step-03:

 

Comparing the results of Step-01 and Step-02, we find-

  • Functional dependencies of set F can determine all the attributes which have been determined by the functional dependencies of set G.
  • Thus, we conclude F covers G i.e. F ⊇ G.

 

Determining whether G covers F-

 

Step-01:

 

  • (A)+ = { A , C , D }               // closure of left side of A → C using set F
  • (AC)+ = { A , C , D }            // closure of left side of AC → D using set F
  • (E)+ = { A , C , D , E , H }    // closure of left side of E → AD and E → H using set F

 

Step-02:

 

  • (A)+ = { A , C , D }                // closure of left side of A → C using set G
  • (AC)+ = { A , C , D }             // closure of left side of AC → D using set G
  • (E)+ = { A , C , D , E , H }    // closure of left side of E → AD and E → H using set G

 

Step-03:

 

Comparing the results of Step-01 and Step-02, we find-

  • Functional dependencies of set G can determine all the attributes which have been determined by the functional dependencies of set F.
  • Thus, we conclude G covers F i.e. G ⊇ F.

 

Determining whether both F and G cover each other-

 

  • From Step-01, we conclude F covers G.
  • From Step-02, we conclude G covers F.
  • Thus, we conclude both F and G cover each other i.e. F = G.

 

Thus, Option (D) is correct.

 

Next Article- Canonical Cover in DBMS

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Normalization in DBMS | Normal Forms

Database Management System

Normalization in DBMS-

 

In DBMS, database normalization is a process of making the database consistent by-

  • Reducing the redundancies
  • Ensuring the integrity of data through lossless decomposition

Normalization is done through normal forms.

 

Normal Forms-

 

The standard normal forms used are-

 

 

  1. First Normal Form (1NF)
  2. Second Normal Form (2NF)
  3. Third Normal Form (3NF)
  4. Boyce-Codd Normal Form (BCNF)

 

There exists several other normal forms even after BCNF but generally we normalize till BCNF only.

 

First Normal Form-

 

A given relation is called in First Normal Form (1NF) if each cell of the table contains only an atomic value.

OR

A given relation is called in First Normal Form (1NF) if the attribute of every tuple is either single valued or a null value.

 

Example-

 

The following relation is not in 1NF-

 

Student_id Name Subjects
100 Akshay Computer Networks, Designing
101 Aman Database Management System
102 Anjali Automata, Compiler Design

Relation is not in 1NF

 

However,

  • This relation can be brought into 1NF.
  • This can be done by rewriting the relation such that each cell of the table contains only one value.

 

Student_id Name Subjects
100 Akshay Computer Networks
100 Akshay Designing
101 Aman Database Management System
102 Anjali Automata
102 Anjali Compiler Design

Relation is in 1NF

 

This relation is in First Normal Form (1NF).

 

NOTE-

 

  • By default, every relation is in 1NF.
  • This is because formal definition of a relation states that value of all the attributes must be atomic.

 

Second Normal Form-

 

A given relation is called in Second Normal Form (2NF) if and only if-

  1. Relation already exists in 1NF.
  2. No partial dependency exists in the relation.

 

Also Read- Functional Dependency in DBMS

 

Partial Dependency

 

A partial dependency is a dependency where few attributes of the candidate key determines non-prime attribute(s).

OR

A partial dependency is a dependency where a portion of the candidate key or incomplete candidate key determines non-prime attribute(s).

 

In other words,

A → B is called a partial dependency if and only if-

  1. A is a subset of some candidate key
  2. B is a non-prime attribute.

If any one condition fails, then it will not be a partial dependency.

 

NOTE-

 

  • To avoid partial dependency, incomplete candidate key must not determine any non-prime attribute.
  • However, incomplete candidate key can determine prime attributes.

 

Also Read- How To Find Candidate Keys?

 

Example-

 

Consider a relation- R ( V , W , X , Y , Z ) with functional dependencies-

VW → XY

Y → V

WX → YZ

 

The possible candidate keys for this relation are-

VW , WX , WY

 

From here,

  • Prime attributes = { V , W , X , Y }
  • Non-prime attributes = { Z }

 

Now, if we observe the given dependencies-

  • There is no partial dependency.
  • This is because there exists no dependency where incomplete candidate key determines any non-prime attribute.

 

Thus, we conclude that the given relation is in 2NF.

 

Third Normal Form-

 

A given relation is called in Third Normal Form (3NF) if and only if-

  1. Relation already exists in 2NF.
  2. No transitive dependency exists for non-prime attributes.

 

Transitive Dependency

 

A → B is called a transitive dependency if and only if-

  1. A is not a super key.
  2. B is a non-prime attribute.

If any one condition fails, then it is not a transitive dependency.

 

NOTE-

 

  • Transitive dependency must not exist for non-prime attributes.
  • However, transitive dependency can exist for prime attributes.

 

OR

 

A relation is called in Third Normal Form (3NF) if and only if-

Any one condition holds for each non-trivial functional dependency A → B

  1. A is a super key
  2. B is a prime attribute

 

Example-

 

Consider a relation- R ( A , B , C , D , E ) with functional dependencies-

A → BC

CD → E

B → D

E → A

 

The possible candidate keys for this relation are-

A , E , CD , BC

 

From here,

  • Prime attributes = { A , B , C , D , E }
  • There are no non-prime attributes

 

Now,

  • It is clear that there are no non-prime attributes in the relation.
  • In other words, all the attributes of relation are prime attributes.
  • Thus, all the attributes on RHS of each functional dependency are prime attributes.

 

Thus, we conclude that the given relation is in 3NF.

 

Boyce-Codd Normal Form-

 

A given relation is called in BCNF if and only if-

  1. Relation already exists in 3NF.
  2. For each non-trivial functional dependency A → B, A is a super key of the relation.

 

Example-

 

Consider a relation- R ( A , B , C ) with the functional dependencies-

A → B

B → C

C → A

 

The possible candidate keys for this relation are-

A , B , C

 

Now, we can observe that RHS of each given functional dependency is a candidate key.

Thus, we conclude that the given relation is in BCNF.

 

Next Article- Important Points About Normal Forms

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.