Category: Data Structures

Hashing in Data Structure | Hash Functions

Data Structures

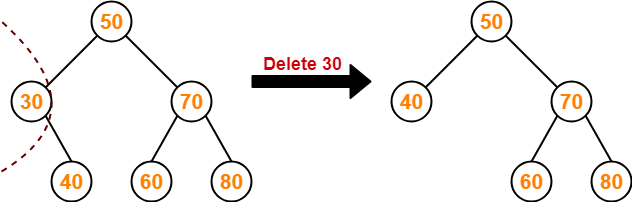
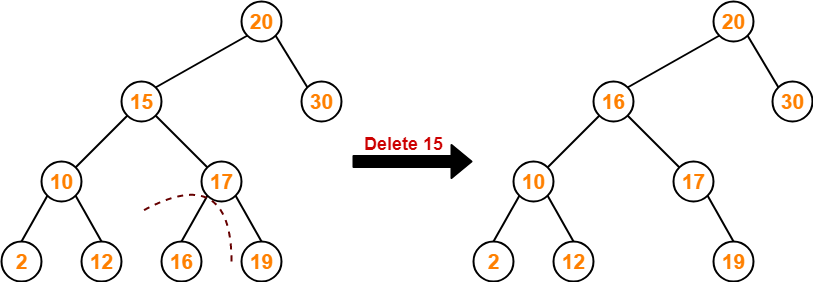
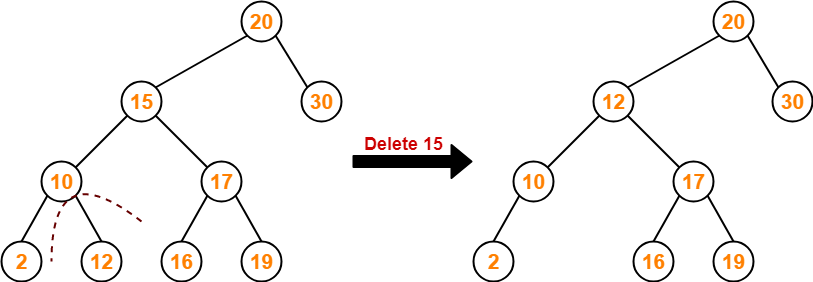
Searching Techniques-

 

In data structures,

  • There are several searching techniques like linear search, binary search, search trees etc.
  • In these techniques, time taken to search any particular element depends on the total number of elements.

 

Example-

 

  • Linear Search takes O(n) time to perform the search in unsorted arrays consisting of n elements.
  • Binary Search takes O(logn) time to perform the search in sorted arrays consisting of n elements.
  • It takes O(logn) time to perform the search in Binary Search Tree consisting of n elements.

 

Drawback-

 

The main drawback of these techniques is-

  • As the number of elements increases, time taken to perform the search also increases.
  • This becomes problematic when total number of elements become too large.

 

Hashing in Data Structure-

 

In data structures,

  • Hashing is a well-known technique to search any particular element among several elements.
  • It minimizes the number of comparisons while performing the search.

 

Advantage-

 

Unlike other searching techniques,

  • Hashing is extremely efficient.
  • The time taken by it to perform the search does not depend upon the total number of elements.
  • It completes the search with constant time complexity O(1).

 

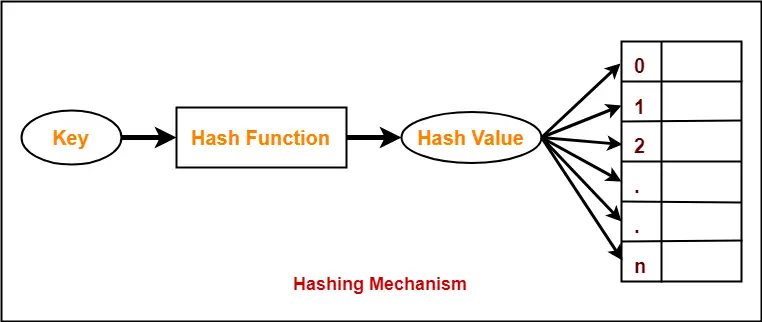
Hashing Mechanism-

 

In hashing,

  • An array data structure called as Hash table is used to store the data items.
  • Based on the hash key value, data items are inserted into the hash table.

 

Hash Key Value-

 

  • Hash key value is a special value that serves as an index for a data item.
  • It indicates where the data item should be be stored in the hash table.
  • Hash key value is generated using a hash function.

 

 

Hash Function-

 

Hash function is a function that maps any big number or string to a small integer value.

 

  • Hash function takes the data item as an input and returns a small integer value as an output.
  • The small integer value is called as a hash value.
  • Hash value of the data item is then used as an index for storing it into the hash table.

 

Types of Hash Functions-

 

There are various types of hash functions available such as-

  1. Mid Square Hash Function
  2. Division Hash Function
  3. Folding Hash Function etc

 

It depends on the user which hash function he wants to use.

 

Properties of Hash Function-

 

The properties of a good hash function are-

  • It is efficiently computable.
  • It minimizes the number of collisions.
  • It distributes the keys uniformly over the table.

 

To gain better understanding about Hashing in Data Structures,

Watch this Video Lecture

 

Next Article- Collision in Hashing

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Tree Insertion | BST Deletion

Data Structures

Binary Search Tree-

 

Before you go through this article, make sure that you have gone through the previous article on Binary Search Trees.

 

Binary search tree (BST) is a special kind of binary tree where each node contains-

  • Only larger values in its right subtree.
  • Only smaller values in its left subtree.

 

In this article, we will discuss about Binary Search Tree Operations.

 

Binary Search Tree Operations-

 

Commonly performed operations on binary search tree are-

 

 

  1. Search Operation
  2. Insertion Operation
  3. Deletion Operation

 

1. Search Operation-

 

Search Operation is performed to search a particular element in the Binary Search Tree.

 

Rules-

 

For searching a given key in the BST,

  • Compare the key with the value of root node.
  • If the key is present at the root node, then return the root node.
  • If the key is greater than the root node value, then recur for the root node’s right subtree.
  • If the key is smaller than the root node value, then recur for the root node’s left subtree.

 

Example-

 

Consider key = 45 has to be searched in the given BST-

 

 

  • We start our search from the root node 25.
  • As 45 > 25, so we search in 25’s right subtree.
  • As 45 < 50, so we search in 50’s left subtree.
  • As 45 > 35, so we search in 35’s right subtree.
  • As 45 > 44, so we search in 44’s right subtree but 44 has no subtrees.
  • So, we conclude that 45 is not present in the above BST.

 

2. Insertion Operation-

 

Insertion Operation is performed to insert an element in the Binary Search Tree.

 

Rules-

 

The insertion of a new key always takes place as the child of some leaf node.

For finding out the suitable leaf node,

  • Search the key to be inserted from the root node till some leaf node is reached.
  • Once a leaf node is reached, insert the key as child of that leaf node.

 

Example-

 

Consider the following example where key = 40 is inserted in the given BST-

 

 

  • We start searching for value 40 from the root node 100.
  • As 40 < 100, so we search in 100’s left subtree.
  • As 40 > 20, so we search in 20’s right subtree.
  • As 40 > 30, so we add 40 to 30’s right subtree.

 

3. Deletion Operation-

 

Deletion Operation is performed to delete a particular element from the Binary Search Tree.

 

When it comes to deleting a node from the binary search tree, following three cases are possible-

 

Case-01: Deletion Of A Node Having No Child (Leaf Node)-

 

Just remove / disconnect the leaf node that is to deleted from the tree.

 

Example-

 

Consider the following example where node with value = 20 is deleted from the BST-

 

 

Case-02: Deletion Of A Node Having Only One Child-

 

Just make the child of the deleting node, the child of its grandparent.

 

Example-

 

Consider the following example where node with value = 30 is deleted from the BST-

 

 

Case-02: Deletion Of A Node Having Two Children-

 

A node with two children may be deleted from the BST in the following two ways-

 

Method-01:

 

  • Visit to the right subtree of the deleting node.
  • Pluck the least value element called as inorder successor.
  • Replace the deleting element with its inorder successor.

 

Example-

 

Consider the following example where node with value = 15 is deleted from the BST-

 

 

Method-02:

 

  • Visit to the left subtree of the deleting node.
  • Pluck the greatest value element called as inorder predecessor.
  • Replace the deleting element with its inorder predecessor.

 

Example-

 

Consider the following example where node with value = 15 is deleted from the BST-

 

 

To gain better understanding about BST Operations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Time Complexity of BST Operations

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.