Data Structures | Gate Vidyalay

Category: Data Structures

AVL Tree | AVL Tree Example | AVL Tree Rotation

Data Structures

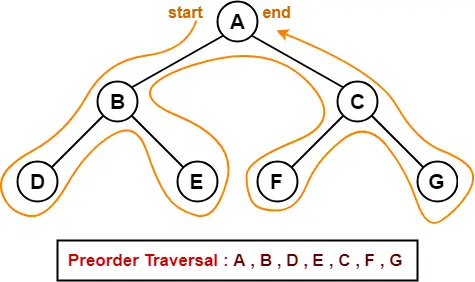
AVL Tree-

AVL trees are special kind of binary search trees.
In AVL trees, height of left subtree and right subtree of every node differs by at most one.
AVL trees are also called as self-balancing binary search trees.

Also Read- Binary Search Trees

Example-

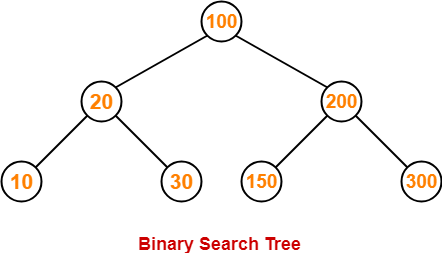
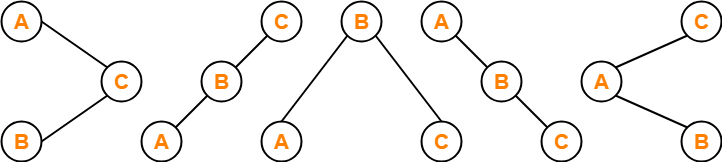
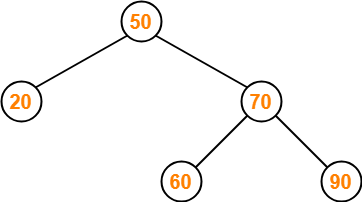
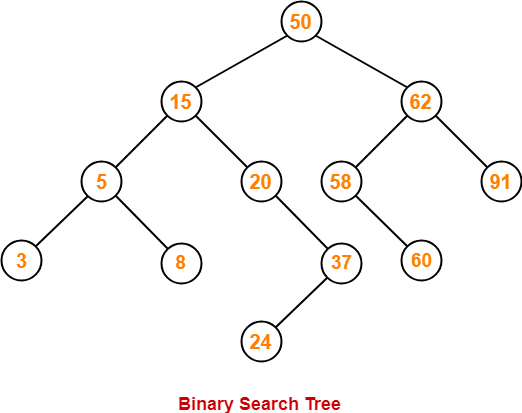
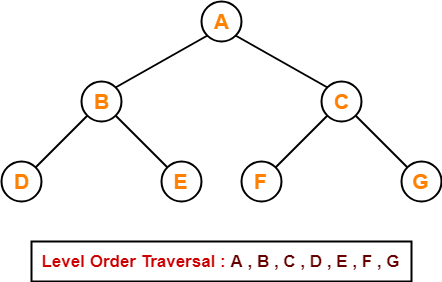
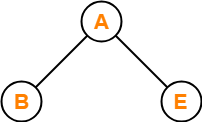
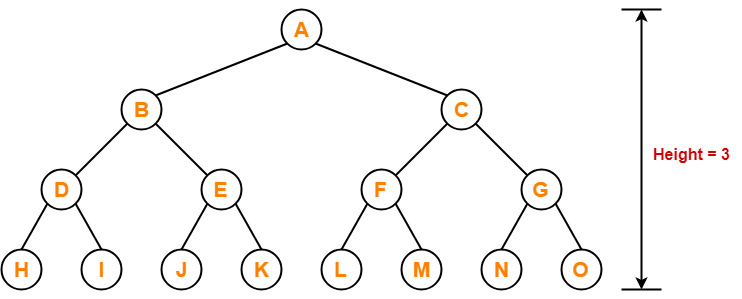
Following tree is an example of AVL tree-

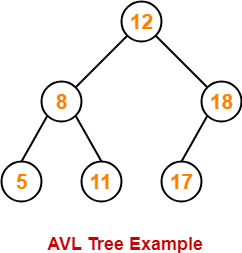
This tree is an AVL tree because-

It is a binary search tree.
The difference between height of left subtree and right subtree of every node is at most one.

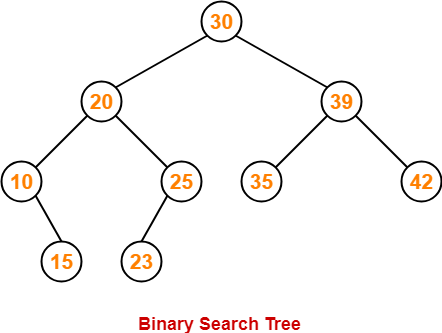
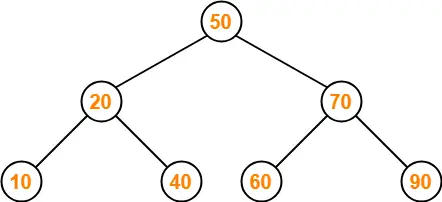
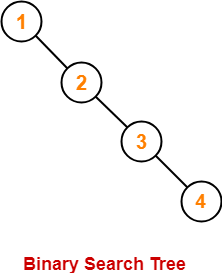
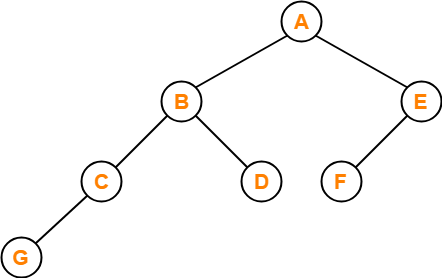
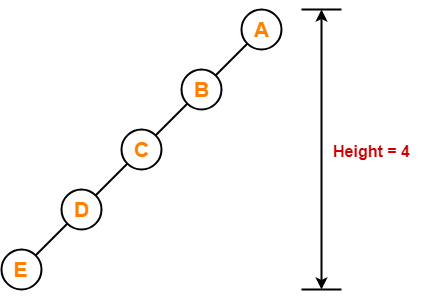
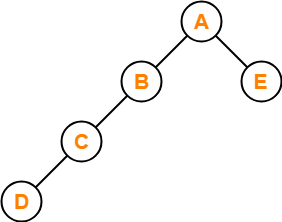
Following tree is not an example of AVL Tree-

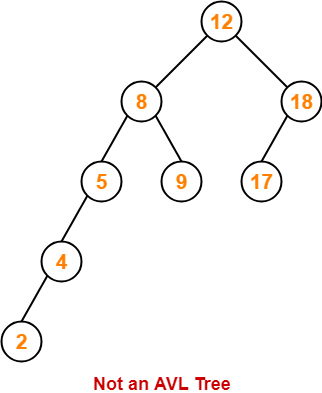
This tree is not an AVL tree because-

The difference between height of left subtree and right subtree of root node = 4 – 2 = 2.
This difference is greater than one.

Balance Factor-

In AVL tree,

Balance factor is defined for every node.
Balance factor of a node = Height of its left subtree – Height of its right subtree

In AVL tree,

Balance factor of every node is either 0 or 1 or -1.

AVL Tree Operations-

Like BST Operations, commonly performed operations on AVL tree are-

Search Operation
Insertion Operation
Deletion Operation

Also Read- Insertion in AVL Tree

After performing any operation on AVL tree, the balance factor of each node is checked.

There are following two cases possible-

Case-01:

After the operation, the balance factor of each node is either 0 or 1 or -1.
In this case, the AVL tree is considered to be balanced.
The operation is concluded.

Case-02:

After the operation, the balance factor of at least one node is not 0 or 1 or -1.
In this case, the AVL tree is considered to be imbalanced.
Rotations are then performed to balance the tree.

AVL Tree Rotations-

Rotation is the process of moving the nodes to make tree balanced.

Kinds of Rotations-

There are 4 kinds of rotations possible in AVL Trees-

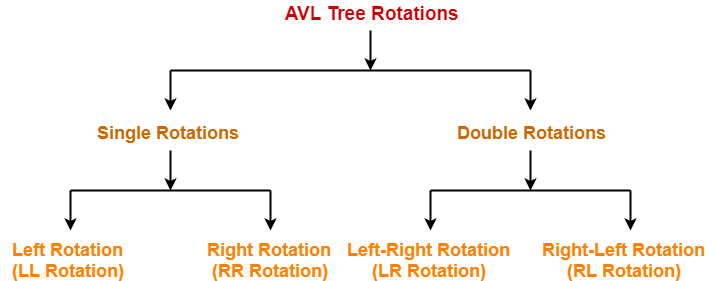
Left Rotation (LL Rotation)
Right Rotation (RR Rotation)
Left-Right Rotation (LR Rotation)
Right-Left Rotation (RL Rotation)

Cases Of Imbalance And Their Balancing Using Rotation Operations-

Case-01:

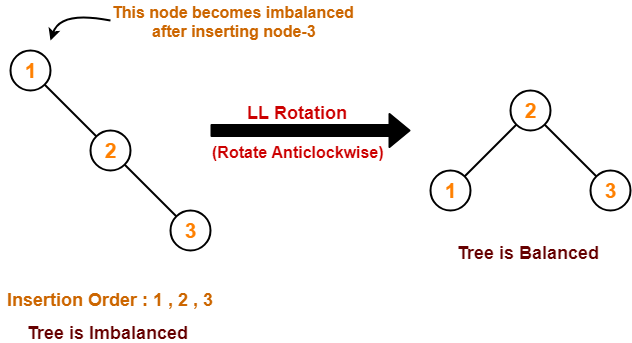
Case-02:

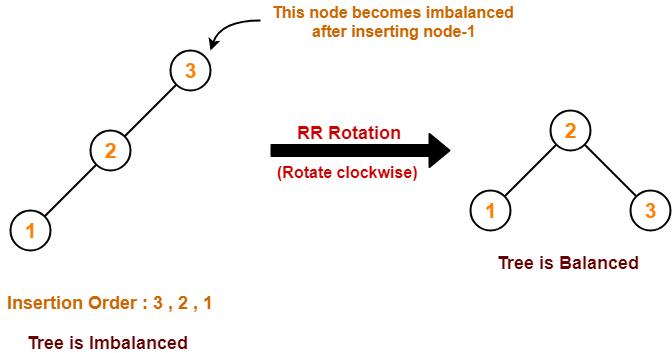
Case-03:

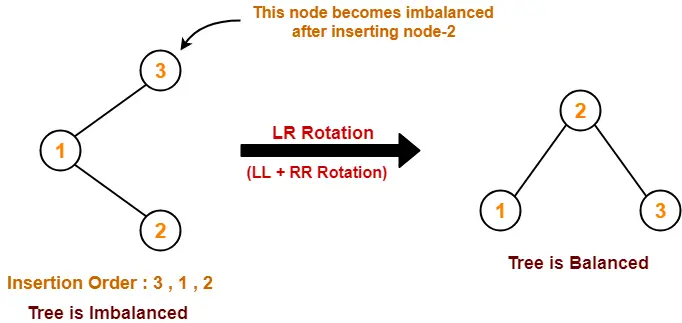
Case-04:

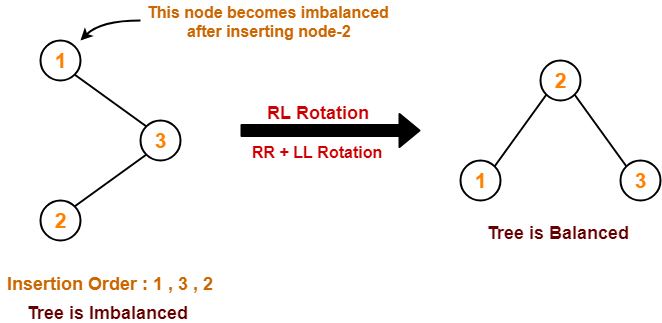
To gain better understanding about AVL Trees and Rotations,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- AVL Tree Properties

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Tree Traversal | BST Traversal

Data Structures

Binary Search Tree-

Before you go through this article, make sure that you have gone through the previous article on Binary Search Trees.

Binary search tree (BST) is a special kind of binary tree where each node contains-

Only larger values in its right subtree.
Only smaller values in its left subtree.

In this article, we will discuss about Binary Search Tree Traversal.

BST Traversal-

A binary search tree is traversed in exactly the same way a binary tree is traversed.
In other words, BST traversal is same as binary tree traversal.

Read More- Binary Tree Traversal

Example-

Consider the following binary search tree-

Now, let us write the traversal sequences for this binary search tree-

Preorder Traversal-

100 , 20 , 10 , 30 , 200 , 150 , 300

Inorder Traversal-

10 , 20 , 30 , 100 , 150 , 200 , 300

Postorder Traversal-

10 , 30 , 20 , 150 , 300 , 200 , 100

Important Notes-

Note-01:

Inorder traversal of a binary search tree always yields all the nodes in increasing order.

Note-02:

Unlike Binary Trees,

A binary search tree can be constructed using only preorder or only postorder traversal result.
This is because inorder traversal can be obtained by sorting the given result in increasing order.

To gain better understanding about Binary Search Tree Traversal,

Watch this Video Lecture

PRACTICE PROBLEMS BASED ON BST TRAVERSAL-

Problem-01:

Suppose the numbers 7 , 5 , 1 , 8 , 3 , 6 , 0 , 9 , 4 , 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the usual ordering on natural numbers.

What is the inorder traversal sequence of the resultant tree?

7 , 5 , 1 , 0 , 3 , 2 , 4 , 6 , 8 , 9
0 , 2 , 4 , 3 , 1 , 6 , 5 , 9 , 8 , 7
0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9
9 , 8 , 6 , 4 , 2 , 3 , 0 , 1 , 5 , 7

Solution-

This given problem may be solved in the following two ways-

Method-01:

We construct a binary search tree for the given elements.
We write the inorder traversal sequence from the binary search tree so obtained.

Following these steps, we have-

Thus, Option (C) is correct.

Method-02:

We know, inorder traversal of a binary search tree always yields all the nodes in increasing order.

Using this result,

We arrange all the given elements in increasing order.
Then, we report the sequence so obtained as inorder traversal sequence.

Inorder Traversal :

0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9

Thus, Option (C) is correct.

Problem-02:

The preorder traversal sequence of a binary search tree is-

30 , 20 , 10 , 15 , 25 , 23 , 39 , 35 , 42

What one of the following is the postorder traversal sequence of the same tree?

10 , 20 , 15 , 23 , 25 , 35 , 42 , 39 , 30
15 , 10 , 25 , 23 , 20 , 42 , 35 , 39 , 30
15 , 20 , 10 , 23 , 25 , 42 , 35 , 39 , 30
15 , 10 , 23 , 25 , 20 , 35 , 42 , 39 , 30

Solution-

In this question,

We are provided with the preorder traversal sequence.
We write the inorder traversal sequence by arranging all the numbers in ascending order.

Then-

Postorder Traversal : 30 , 20 , 10 , 15 , 25 , 23 , 39 , 35 , 42
Inorder Traversal : 10 , 15 , 20 , 23 , 25 , 30 , 35 , 39 , 42

Now,

We draw a binary search tree using these traversal results.
The binary search tree so obtained is as shown-

Now, we write the postorder traversal sequence-

Postorder Traversal :

15 , 10 , 23 , 25, 20, 35, 42, 39, 30

Thus, Option (D) is correct.

To watch video solutions and practice more problems,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Binary Search Tree Operations

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Tree | Example | Construction

Data Structures

Binary Tree-

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

We have discussed-

Binary tree is a special tree data structure.
In a binary tree, each node can have at most 2 children.
In a binary tree, nodes may be arranged in any random order.

In this article, we will discuss about Binary Search Trees.

Binary Search Tree-

Binary Search Tree is a special kind of binary tree in which nodes are arranged in a specific order.

In a binary search tree (BST), each node contains-

Only smaller values in its left sub tree
Only larger values in its right sub tree

Example-

Number of Binary Search Trees-

Example-

Number of distinct binary search trees possible with 3 distinct keys

= ^2×3C₃ / 3+1

= ⁶C₃ / 4

= 5

If three distinct keys are A, B and C, then 5 distinct binary search trees are-

Binary Search Tree Construction-

Let us understand the construction of a binary search tree using the following example-

Example-

Construct a Binary Search Tree (BST) for the following sequence of numbers-

50, 70, 60, 20, 90, 10, 40, 100

When elements are given in a sequence,

Always consider the first element as the root node.
Consider the given elements and insert them in the BST one by one.

The binary search tree will be constructed as explained below-

Insert 50-

Insert 70-

As 70 > 50, so insert 70 to the right of 50.

Insert 60-

As 60 > 50, so insert 60 to the right of 50.
As 60 < 70, so insert 60 to the left of 70.

Insert 20-

As 20 < 50, so insert 20 to the left of 50.

Insert 90-

As 90 > 50, so insert 90 to the right of 50.
As 90 > 70, so insert 90 to the right of 70.

Insert 10-

As 10 < 50, so insert 10 to the left of 50.
As 10 < 20, so insert 10 to the left of 20.

Insert 40-

As 40 < 50, so insert 40 to the left of 50.
As 40 > 20, so insert 40 to the right of 20.

Insert 100-

As 100 > 50, so insert 100 to the right of 50.
As 100 > 70, so insert 100 to the right of 70.
As 100 > 90, so insert 100 to the right of 90.

This is the required Binary Search Tree.

To gain better understanding about Binary Search Trees,

Watch this Video Lecture

PRACTICE PROBLEMS BASED ON BINARY SEARCH TREES-

Problem-01:

A binary search tree is generated by inserting in order of the following integers-

50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24

The number of nodes in the left subtree and right subtree of the root respectively is _____.

(4, 7)
(7, 4)
(8, 3)
(3, 8)

Solution-

Using the above discussed steps, we will construct the binary search tree.

The resultant binary search tree will be-

Clearly,

Number of nodes in the left subtree of the root = 7
Number of nodes in the right subtree of the root = 4

Thus, Option (B) is correct.

Problem-02:

How many distinct binary search trees can be constructed out of 4 distinct keys?

Solution-

Number of distinct binary search trees possible with 4 distinct keys

= ²ⁿC_n / n+1

= ^2×4C₄ / 4+1

= ⁸C₄ / 5

= 14

Thus, Option (B) is correct.

Problem-03:

The numbers 1, 2, …, n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be-

p
p+1
n-p
n-p+1

Solution-

Let n = 4 and p = 3.

Then, given options reduce to-

Our binary search tree will be as shown-

Clearly, first inserted number = 1.

Thus, Option (C) is correct.

Problem-04:

We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with given set so that it becomes a binary search tree?

0
1
n!
C(2n, n) / n+1

Solution-

Option (B) is correct.

To watch video solutions and practice more problems,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Binary Search Tree Traversal

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Tree Traversal | Binary Tree Traversal

Data Structures

Binary Tree-

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

We have discussed-

Binary tree is a special tree data structure.
In a binary tree, each node can have at most 2 children.

In this article, we will discuss about Binary Tree Traversal.

Tree Traversal-

Tree Traversal refers to the process of visiting each node in a tree data structure exactly once.

Various tree traversal techniques are-

Depth First Traversal-

Following three traversal techniques fall under Depth First Traversal-

Preorder Traversal
Inorder Traversal
Postorder Traversal

1. Preorder Traversal-

Algorithm-

Visit the root
Traverse the left sub tree i.e. call Preorder (left sub tree)
Traverse the right sub tree i.e. call Preorder (right sub tree)

Root → Left → Right

Example-

Consider the following example-

Preorder Traversal Shortcut

Traverse the entire tree starting from the root node keeping yourself to the left.

Applications-

Preorder traversal is used to get prefix expression of an expression tree.
Preorder traversal is used to create a copy of the tree.

2. Inorder Traversal-

Algorithm-

Traverse the left sub tree i.e. call Inorder (left sub tree)
Visit the root
Traverse the right sub tree i.e. call Inorder (right sub tree)

Left → Root → Right

Example-

Consider the following example-

Inorder Traversal Shortcut

Keep a plane mirror horizontally at the bottom of the tree and take the projection of all the nodes.

Application-

Inorder traversal is used to get infix expression of an expression tree.

3. Postorder Traversal-

Algorithm-

Traverse the left sub tree i.e. call Postorder (left sub tree)
Traverse the right sub tree i.e. call Postorder (right sub tree)
Visit the root

Left → Right → Root

Example-

Consider the following example-

Postorder Traversal Shortcut

Pluck all the leftmost leaf nodes one by one.

Applications-

Postorder traversal is used to get postfix expression of an expression tree.
Postorder traversal is used to delete the tree.
This is because it deletes the children first and then it deletes the parent.

Breadth First Traversal-

Breadth First Traversal of a tree prints all the nodes of a tree level by level.
Breadth First Traversal is also called as Level Order Traversal.

Example-

Application-

Level order traversal is used to print the data in the same order as stored in the array representation of a complete binary tree.

To gain better understanding about Tree Traversal,

Watch this Video Lecture

Also Read- Binary Tree Properties

PRACTICE PROBLEMS BASED ON TREE TRAVERSAL-

Problem-01:

If the binary tree in figure is traversed in inorder, then the order in which the nodes will be visited is ____?

Solution-

The inorder traversal will be performed as-

Problem-02:

Which of the following sequences denotes the postorder traversal sequence of the tree shown in figure?

FEGCBDBA
GCBDAFE
GCDBFEA
FDEGCBA

Solution-

Perform the postorder traversal by plucking all the leftmost leaf nodes one by one.

Then,

Postorder Traversal : G , C , D , B , F , E , A

Thus, Option (C) is correct.

Problem-03:

Let LASTPOST, LASTIN, LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal respectively of a complete binary tree. Which of the following is always true?

LASTIN = LASTPOST
LASTIN = LASTPRE
LASTPRE = LASTPOST
None of these

Solution-

Consider the following complete binary tree-

Preorder Traversal : B , A , E

Inorder Traversal : B , A , E

Postorder Traversal : B , E , A

Clearly, LASTIN = LASTPRE.

Thus, Option (B) is correct.

Problem-04:

Which of the following binary trees has its inorder and preorder traversals as BCAD and ABCD respectively-

Solution-

Option (D) is correct.

To watch video solutions and practice more problems,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Binary Search Trees

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Tree | Binary Tree Properties

Data Structures

Binary Tree-

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

We have discussed-

Binary tree is a special tree data structure.
In a binary tree, each node can have at most 2 children.
There are following types of binary trees-

In this article, we will discuss properties of binary trees.

Binary Tree Properties-

Important properties of binary trees are-

Property-01:

Minimum number of nodes in a binary tree of height H

= H + 1

Example-

To construct a binary tree of height = 4, we need at least 4 + 1 = 5 nodes.

Property-02:

Maximum number of nodes in a binary tree of height H

= 2^H+1 – 1

Example-

Maximum number of nodes in a binary tree of height 3

= 2³⁺¹ – 1

= 16 – 1

= 15 nodes

Thus, in a binary tree of height = 3, maximum number of nodes that can be inserted = 15.

We can not insert more number of nodes in this binary tree.

Property-03:

Total Number of leaf nodes in a Binary Tree

= Total Number of nodes with 2 children + 1

Example-

Consider the following binary tree-

Here,

Number of leaf nodes = 3
Number of nodes with 2 children = 2

Clearly, number of leaf nodes is one greater than number of nodes with 2 children.

This verifies the above relation.

NOTE

It is interesting to note that-

Number of leaf nodes in any binary tree depends only on the number of nodes with 2 children.

Property-04:

Maximum number of nodes at any level ‘L’ in a binary tree

= 2^L

Example-

Maximum number of nodes at level-2 in a binary tree

= 2²

= 4

Thus, in a binary tree, maximum number of nodes that can be present at level-2 = 4.

To gain better understanding about Binary Tree Properties,

Watch this Video Lecture

PRACTICE PROBLEMS BASED ON BINARY TREE PROPERTIES-

Problem-01:

A binary tree T has n leaf nodes. The number of nodes of degree-2 in T is ______?

log₂n
n-1
n
2ⁿ

Solution-

Using property-3, we have-

Number of degree-2 nodes

= Number of leaf nodes – 1

= n – 1

Thus, Option (B) is correct.

Problem-02:

In a binary tree, for every node the difference between the number of nodes in the left and right subtrees is at most 2. If the height of the tree is h > 0, then the minimum number of nodes in the tree is ______?

2^h-1
2^h-1 + 1
2^h – 1
2^h

Solution-

Let us assume any random value of h. Let h = 3.

Then the given options reduce to-

Now, consider the following binary tree with height h = 3-

This binary tree satisfies the question constraints.
It is constructed using minimum number of nodes.

Thus, Option (B) is correct.

Problem-03:

In a binary tree, the number of internal nodes of degree-1 is 5 and the number of internal nodes of degree-2 is 10. The number of leaf nodes in the binary tree is ______?

Solution-

Using property-3, we have-

Number of leaf nodes in a binary tree

= Number of degree-2 nodes + 1

= 10 + 1

= 11

Thus, Option (B) is correct.

Problem-04:

The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is ______?