Category: Data Structures

Heap Operations | Max Heap Operations | Examples

Data Structures

Heap Data Structure-

 

Before you go through this article, make sure that you have gone through the previous article on Heap Data Structure.

 

We have discussed-

  • Heap is a specialized data structure with special properties.
  • A binary heap is a binary tree that has ordering and structural properties.
  • A heap may be a max heap or a min heap.

 

In this article, we will discuss about heap operations.

 

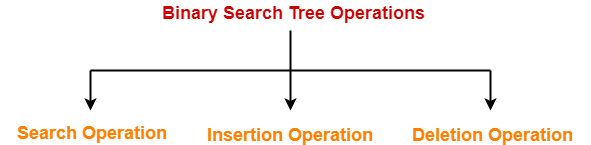
Heap Operations-

 

The most basic and commonly performed operations on a heap are-

 

 

  1. Search Operation
  2. Insertion Operation
  3. Deletion Operation

 

Here, we will discuss how these operations are performed on a max heap.

 

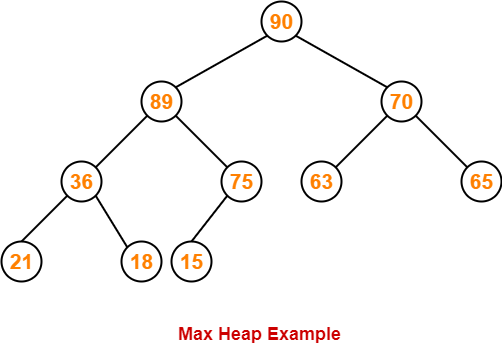
Max Heap-

 

  • In max heap, every node contains greater or equal value element than its child nodes.
  • Thus, root node contains the largest value element.

 

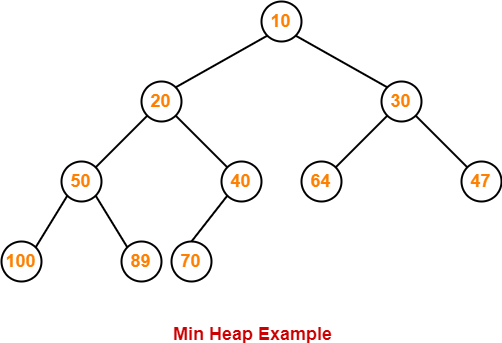
Example-

 

The following heap is an example of a max heap-

 

 

Max Heap Operations-

 

We will discuss the construction of a max heap and how following operations are performed on a max heap-

  • Finding Maximum Operation
  • Insertion Operation
  • Deletion Operation

 

Max Heap Construction-

 

Given an array of elements, the steps involved in constructing a max heap are-

 

Step-01:

 

Convert the given array of elements into an almost complete binary tree.

 

Step-02:

 

Ensure that the tree is a max heap.

  • Check that every non-leaf node contains a greater or equal value element than its child nodes.
  • If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
  • Start checking from a non-leaf node with the highest index (bottom to top and right to left).

 

Finding Maximum Operation-

 

  • In max heap, the root node always contains the maximum value element.
  • So, we directly display the root node value as maximum value in max heap.

 

Insertion Operation-

 

Insertion Operation is performed to insert an element in the heap tree.

 

The steps involved in inserting an element are-

 

Step-01:

 

Insert the new element as a next leaf node from left to right.

 

Step-02:

 

Ensure that the tree remains a max heap.

  • Check that every non-leaf node contains a greater or equal value element than its child nodes.
  • If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
  • Start checking from a non-leaf node with the highest index (bottom to top and right to left).

 

Deletion Operation-

 

Deletion Operation is performed to delete a particular element from the heap tree.

 

When it comes to deleting a node from the heap tree, following two cases are possible-

 

Case-01: Deletion Of Last Node-

 

  • This case is pretty simple.
  • Just remove / disconnect the last leaf node from the heap tree.

 

Case-02: Deletion Of Some Other Node-

 

  • This case is little bit difficult.
  • Deleting a node other than the last node disturbs the heap properties.

 

The steps involved in deleting such a node are-

 

Step-01:

 

  • Delete the desired element from the heap tree.
  • Pluck the last node and put in place of the deleted node.

 

Step-02:

 

Ensure that the tree remains a max heap.

  • Check that every non-leaf node contains a greater or equal value element than its child nodes.
  • If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
  • Start checking from a non-leaf node with the highest index (bottom to top and right to left).

 

PRACTICE PROBLEMS BASED ON MAX HEAP OPERATIONS-

 

Problem-01:

 

Construct a max heap for the given array of elements-

1, 5, 6, 8, 12, 14, 16

 

Solution-

 

Step-01:

 

We convert the given array of elements into an almost complete binary tree-

 

 

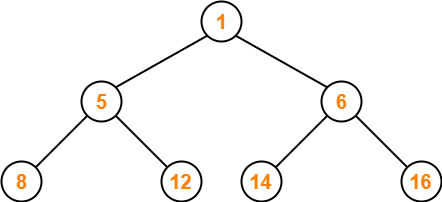
Step-02:

 

  • We ensure that the tree is a max heap.
  • Node 6 contains greater element in its right child node.
  • So, we swap node 6 and node 16.

 

The resulting tree is-

 

 

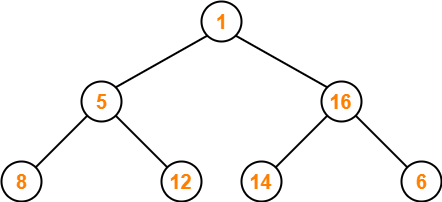
Step-03:

 

  • Node 5 contains greater element in its right child node.
  • So, we swap node 5 and node 12.

 

The resulting tree is-

 

 

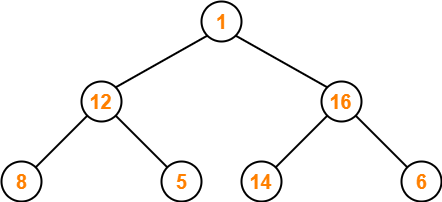
Step-04:

 

  • Node 1 contains greater element in its right child node.
  • So, we swap node 1 and node 16.

 

The resulting tree is-

 

 

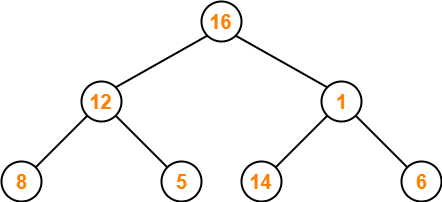
Step-05:

 

  • Node 1 contains greater element in its left child node.
  • So, we swap node 1 and node 14.

 

The resulting tree is-

 

 

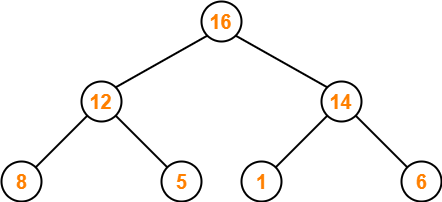
This is the required max heap for the given array of elements.

 

Problem-02:

 

Consider the following max heap-

50, 30, 20, 15, 10, 8, 16

Insert a new node with value 60.

 

Solution-

 

Step-01:

 

We convert the given array of elements into a heap tree-

 

 

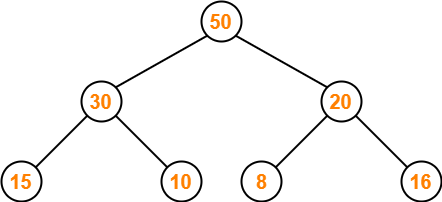
Step-02:

 

We insert the new element 60 as a next leaf node from left to right.

The resulting tree is-

 

 

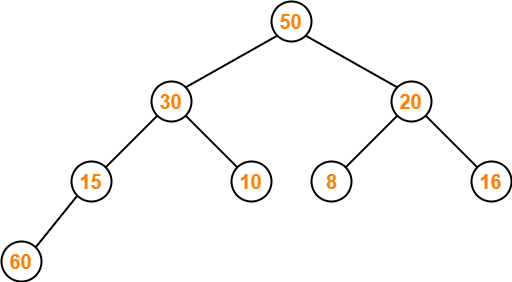
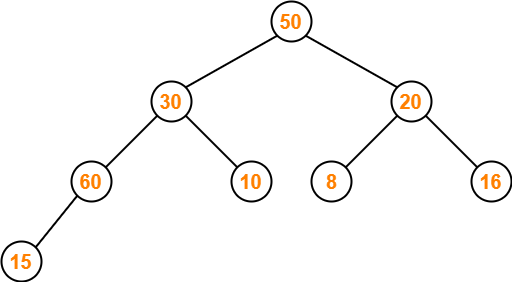
Step-03:

 

  • We ensure that the tree is a max heap.
  • Node 15 contains greater element in its left child node.
  • So, we swap node 15 and node 60.

 

The resulting tree is-

 

 

Step-04:

 

  • Node 30 contains greater element in its left child node.
  • So, we swap node 30 and node 60.

 

The resulting tree is-

 

 

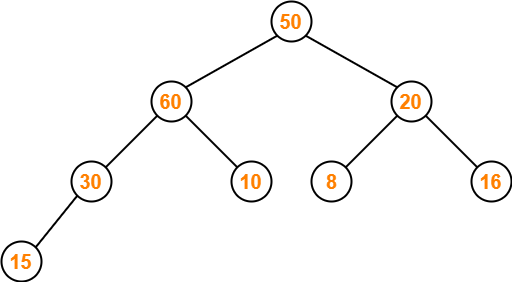
Step-05:

 

  • Node 50 contains greater element in its left child node.
  • So, we swap node 50 and node 60.

 

The resulting tree is-

 

 

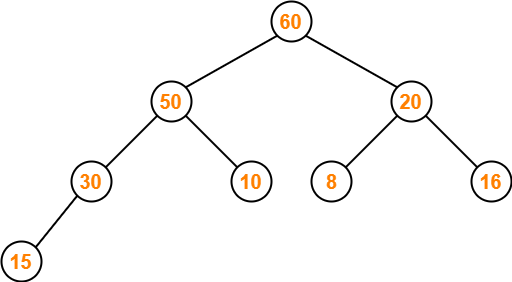
This is the required max heap after inserting the node with value 60.

 

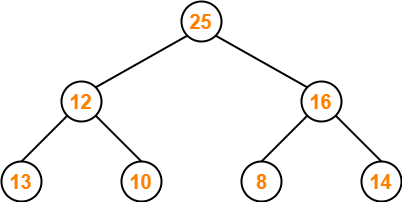
Problem-03:

 

Consider the following max heap-

50, 30, 20, 15, 10, 8, 16

Delete a node with value 50.

 

Solution-

 

Step-01:

 

We convert the given array of elements into a heap tree-

 

 

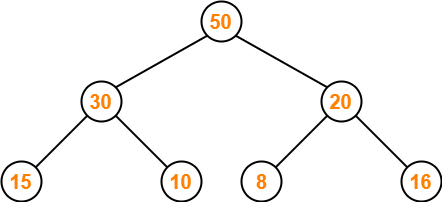
Step-02:

 

  • We delete the element 50 which is present at root node.
  • We pluck the last node 16 and put in place of the deleted node.

 

The resulting tree is-

 

 

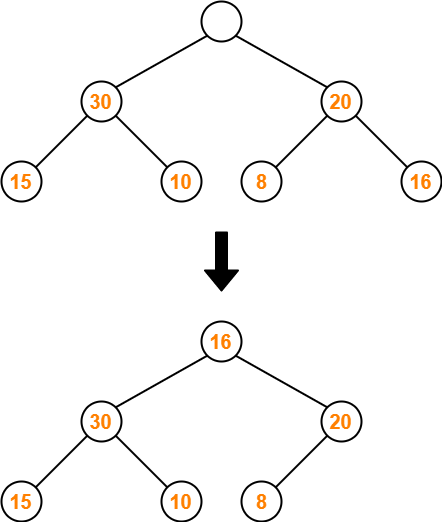
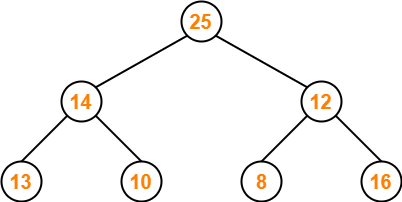
Step-03:

 

  • We ensure that the tree is a max heap.
  • Node 16 contains greater element in its left child node.
  • So, we swap node 16 and node 30.

 

The resulting tree is-

 

 

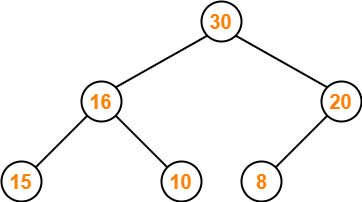
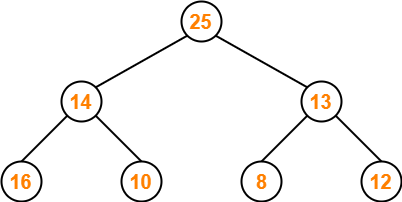
This is the required max heap after deleting the node with value 50.

 

To gain better understanding about Heap Data Structure,

Watch this Video Lecture

 

Next Article- Introduction to Hashing

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Heap Data Structure | Binary Heap | Examples

Data Structures

Heap Data Structure-

 

In data structures,

  • Heap is a specialized data structure.
  • It has special characteristics.
  • A heap may be implemented using a n-ary tree.

 

In this article, we will discuss implementation of heap using a binary tree.

 

Binary Heap-

 

A binary heap is a Binary Tree with the following two properties-

 

 

  • Ordering Property
  • Structural Property

 

1. Ordering Property-

 

By this property,

  • Elements in the heap tree are arranged in specific order.
  • This gives rise to two types of heaps- min heap and max heap.

 

2. Structural Property-

 

By this property,

  • Binary heap is an almost complete binary tree.
  • It has all its levels completely filled except possibly the last level.
  • The last level is strictly filled from left to right.

 

Types of Binary Heap-

 

Depending on the arrangement of elements, a binary heap may be of following two types-

 

 

  1. Max Heap
  2. Min Heap

 

1. Max Heap-

 

  • Max Heap conforms to the above properties of heap.
  • In max heap, every node contains greater or equal value element than its child nodes.
  • Thus, root node contains the largest value element.

 

Example-

 

Consider the following example of max heap-

 

 

This is max heap because-

  • Every node contains greater or equal value element than its child nodes.
  • It is an almost complete binary tree with its last level strictly filled from left to right.

 

2. Min Heap-

 

  • Min Heap conforms to the above properties of heap.
  • In min heap, every node contains lesser value element than its child nodes.
  • Thus, root node contains the smallest value element.

 

Example-

 

Consider the following example of min heap-

 

 

This is min heap because-

  • Every node contains lesser value element than its child nodes.
  • It is an almost complete binary tree with its last level strictly filled from left to right.

 

Array Representation of Binary Heap-

 

A binary heap is typically represented as an array.

 

 

For a node present at index ‘i’ of the array Arr-

 

If indexing starts with 0,

  • Its parent node will be present at array location = Arr [ i/2 ]
  • Its left child node will be present at array location = Arr [ 2i+1 ]
  • Its right child node will be present at array location = Arr [ 2i+2 ]

 

If indexing starts with 1,

  • Its parent node will be present at array location = Arr [ ⌊i/2⌋ ]
  • Its left child node will be present at array location = Arr [ 2i ]
  • Its right child node will be present at array location = Arr [ 2i+1 ]

 

Important Notes-

 

Note-01:

 

  • Level order traversal technique may be used to achieve the array representation of a heap tree.
  • Array representation of a heap never contains any empty indices in between.
  • However, array representation of a binary tree may contain some empty indices in between.

 

Note-02:

 

Given an array representation of a binary heap,

  • If all the elements are in descending order, then heap is definitely a max heap.
  • If all the elements are not in descending order, then it may or may not be a max heap.
  • If all the elements are in ascending order, then heap is definitely a min heap.
  • If all the elements are not in ascending order, then it may or may not be a min heap.

 

Note-03:

 

  • In max heap, every node contains greater or equal value element than all its descendants.
  • In min heap, every node contains smaller value element that all its descendants.

 

PRACTICE PROBLEMS BASED ON HEAP DATA STRUCTURE-

 

Problems-

 

Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap? (GATE CS 2009)

  1. 25, 14, 16, 13, 10, 8, 12
  2. 25, 12, 16, 13, 10, 8, 14
  3. 25, 14, 12, 13, 10, 8, 16
  4. 25, 14, 13, 16, 10, 8, 12

 

Solutions-

 

Part-01: 25, 14, 16, 13, 10, 8, 12-

 

The given array representation may be converted into the following structure-

 

 

Clearly,

  • It is a complete binary tree.
  • Every node contains a greater value element than its child nodes.

 

Thus, the given array represents a max heap.

 

Part-02: 25, 12, 16, 13, 10, 8, 14-

 

The given array representation may be converted into the following structure-

 

 

Clearly,

  • It is a complete binary tree.
  • Every node does not contain a greater value element than its child nodes. (Node 12)
  • So, it is not a max heap.
  • Every node does not contain a smaller value element than its child nodes.
  • So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

Part-03: 25, 14, 12, 13, 10, 8, 16-

 

The given array representation may be converted into the following structure-

 

 

Clearly,

  • It is a complete binary tree.
  • Every node does not contain a greater value element than its child nodes. (Node 12)
  • So, it is not a max heap.
  • Every node does not contain a smaller value element than its child nodes.
  • So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

Part-04: 25, 14, 13, 16, 10, 8, 12-

 

The given array representation may be converted into the following structure-

 

 

Clearly,

  • It is a complete binary tree.
  • Every node does not contain a greater value element than its child nodes. (Node 14)
  • So, it is not a max heap.
  • Every node does not contain a smaller value element than its child nodes.
  • So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

To gain better understanding about Heap Data Structure,

Watch this Video Lecture

 

Next Article- Heap Operations

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

AVL Tree Properties | Problems on AVL Tree

Data Structures

AVL Tree-

 

Before you go through this article, make sure that you have gone through the previous article on AVL Trees.

 

We have discussed-

  • AVL trees are self-balancing binary search trees.
  • In AVL trees, balancing factor of each node is either 0 or 1 or -1.

 

In this article, we will discuss AVL Tree Properties.

 

AVL Tree Properties-

 

Important properties of AVL tree are-

 

Property-01:

 

Maximum possible number of nodes in AVL tree of height H

= 2H+1 – 1

 

Example-

 

Maximum possible number of nodes in AVL tree of height-3

= 23+1 – 1

= 16 – 1

= 15

Thus, in AVL tree of height-3, maximum number of nodes that can be inserted = 15.

 

 

We can not insert more number of nodes in this AVL tree.

 

Property-02:

 

Minimum number of nodes in AVL Tree of height H is given by a recursive relation-

N(H) = N(H-1) + N(H-2) + 1

 

Base conditions for this recursive relation are-

  • N(0) = 1
  • N(1) = 2

 

Example-

 

Minimum possible number of nodes in AVL tree of height-3 = 7

 

 

(For explanation, Refer problem-01)

 

Property-03:

 

Minimum possible height of AVL Tree using N nodes

= ⌊log2N⌋

 

Example-

 

Minimum possible height of AVL Tree using 8 nodes

= ⌊log28⌋

= ⌊log223⌋

= ⌊3log22⌋

= ⌊3⌋

= 3

 

Property-04:

 

Maximum height of AVL Tree using N nodes is calculated using recursive relation-

N(H) = N(H-1) + N(H-2) + 1

 

Base conditions for this recursive relation are-

  • N(0) = 1
  • N(1) = 2

 

NOTE-

 

  • If there are n nodes in AVL Tree, its maximum height can not exceed 1.44log2n.
  • In other words, Worst case height of AVL Tree with n nodes = 1.44log2n.

 

PRACTICE PROBLEMS BASED ON AVL TREE PROPERTIES-

 

Problem-01:

 

Find the minimum number of nodes required to construct AVL Tree of height = 3.

 

Solution-

 

We know, minimum number of nodes in AVL tree of height H is given by a recursive relation-

 

N(H) = N(H-1) + N(H-2) + 1

 

where N(0) = 1 and N(1) = 2

 

Step-01:

 

Substituting H = 3 in the recursive relation, we get-

N(3) = N(3-1) + N(3-2) + 1

N(3) = N(2) + N(1) + 1

N(3) = N(2) + 2 + 1                (Using base condition)

N(3) = N(2) + 3                      …………(1)

 

To solve this recursive relation, we need the value of N(2).

 

Step-02:

 

Substituting H = 2 in the recursive relation, we get-

N(2) = N(2-1) + N(2-2) + 1

N(2) = N(1) + N(0) + 1

N(2) = 2 + 1 + 1                 (Using base conditions)

∴ N(2) = 4                          …………(2)

 

Step-03:

 

Using (2) in (1), we get-

N(3) = 4 + 3

∴ N(3) = 7

Thus, minimum number of nodes required to construct AVL tree of height-3 = 7.

 

Problem-02:

 

Find the minimum number of nodes required to construct AVL Tree of height = 4.

 

Solution-

 

We know, minimum number of nodes in AVL tree of height H is given by a recursive relation-

 

N(H) = N(H-1) + N(H-2) + 1

 

where N(0) = 1 and N(1) = 2

 

Step-01:

 

Substituting H = 4 in the recursive relation, we get-

N(4) = N(4-1) + N(4-2) + 1

N(4) = N(3) + N(2) + 1               …………(1)

 

To solve this recursive relation, we need the value of N(2) and N(3).

 

Step-02:

 

Substituting H = 2 in the recursive relation, we get-

N(2) = N(2-1) + N(2-2) + 1

N(2) = N(1) + N(0) + 1

N(2) = 2 + 1 + 1                 (Using base conditions)

∴ N(2) = 4                          …………(2)

 

Step-03:

 

Substituting H = 3 in the recursive relation, we get-

N(3) = N(3-1) + N(3-2) + 1

N(3) = N(2) + N(1) + 1

N(3) = 4 + 2 + 1                 (Using (2) and base condition)

∴ N(3) = 7                          …………(3)

 

Step-04:

 

Using (2) and (3) in (1), we get-

N(4) = 7 + 4 + 1

∴ N(4) = 12

Thus, minimum number of nodes required to construct AVL tree of height-4 = 12.

 

Problem-03:

 

What is the maximum height of any AVL tree with 10 nodes?

 

Solution-

 

For calculating the maximum height of AVL tree with n nodes, we use a recursive relation-

 

N(H) = N(H-1) + N(H-2) + 1

 

Step-01:

 

Substituting H = 2 in the recursive relation, we get-

N(2) = N(2-1) + N(2-2) + 1

N(2) = N(1) + N(0) + 1

N(2) = 2 + 1 + 1                (Using base conditions)

∴ N(2) = 4                          …………(1)

 

So, minimum number of nodes required to construct AVL tree of height-2 = 4.

 

Step-02:

 

Substituting H = 3 in the recursive relation, we get-

N(3) = N(3-1) + N(3-2) + 1

N(3) = N(2) + N(1) + 1

N(3) = 4 + 2 + 1                (Using (1) and base condition)

∴ N(3) = 7                          …………(2)

 

So, minimum number of nodes required to construct AVL tree of height-3 = 7.

 

Step-03:

 

Substituting H = 4 in the recursive relation, we get-

N(4) = N(4-1) + N(4-2) + 1

N(4) = N(3) + N(2) + 1

N(4) = 7 + 4 + 1                (Using (1) and (2))

∴ N(4) = 12

 

So, minimum number of nodes required to construct AVL tree of height-4 = 12.

 

But given number of nodes = 10 which is less than 12.

Thus, maximum height of AVL tree that can be obtained using 10 nodes = 3.

 

Problem-04:

 

What is the maximum height of any AVL tree with 77 nodes?

 

Solution-

 

For calculating the maximum height of AVL tree with n nodes, we use a recursive relation-

 

N(H) = N(H-1) + N(H-2) + 1

 

Step-01:

 

Substituting H = 2 in the recursive relation, we get-

N(2) = N(2-1) + N(2-2) + 1

N(2) = N(1) + N(0) + 1

N(2) = 2 + 1 + 1                (Using base conditions)

∴ N(2) = 4                          …………(1)

 

So, minimum number of nodes required to construct AVL tree of height-2 = 4.

 

Step-02:

 

Substituting H = 3 in the recursive relation, we get-

N(3) = N(3-1) + N(3-2) + 1

N(3) = N(2) + N(1) + 1

N(3) = 4 + 2 + 1                (Using (1) and base condition)

∴ N(3) = 7                          …………(2)

 

So, minimum number of nodes required to construct AVL tree of height-3 = 7.

 

Step-03:

 

Substituting H = 4 in the recursive relation, we get-

N(4) = N(4-1) + N(4-2) + 1

N(4) = N(3) + N(2) + 1

N(4) = 7 + 4 + 1                (Using (1) and (2))

∴ N(4) = 12                        …………(3)

 

So, minimum number of nodes required to construct AVL tree of height-4 = 12.

 

Step-04:

 

Substituting H = 5 in the recursive relation, we get-

N(5) = N(5-1) + N(5-2) + 1

N(5) = N(4) + N(3) + 1

N(5) = 12 + 7 + 1                (Using (2) and (3))

∴ N(5) = 20                          …………(4)

 

So, minimum number of nodes required to construct AVL tree of height-5 = 20.

 

Step-05:

 

Substituting H = 6 in the recursive relation, we get-

N(6) = N(6-1) + N(6-2) + 1

N(6) = N(5) + N(4) + 1

N(6) = 20 + 12 + 1                (Using (3) and (4))

∴ N(6) = 33                            …………(5)

 

So, minimum number of nodes required to construct AVL tree of height-6 = 33.

 

Step-06:

 

Substituting H = 7 in the recursive relation, we get-

N(7) = N(7-1) + N(7-2) + 1

N(7) = N(6) + N(5) + 1

N(7) = 33 + 20 + 1                (Using (4) and (5))

∴ N(7) = 54                            …………(6)

 

So, minimum number of nodes required to construct AVL tree of height-7 = 54.

 

Step-07:

 

Substituting H = 8 in the recursive relation, we get-

N(8) = N(8-1) + N(8-2) + 1

N(8) = N(7) + N(6) + 1

N(8) = 54 + 33 + 1                (Using (5) and (6))

∴ N(8) = 88                            …………(6)

 

So, minimum number of nodes required to construct AVL tree of height-8 = 88.

 

But given number of nodes = 77 which is less than 88.

Thus, maximum height of AVL tree that can be obtained using 77 nodes = 7.

 

Next Article- Insertion in AVL Tree

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

AVL Tree Insertion | Insertion in AVL Tree

Data Structures

AVL Tree-

 

Before you go through this article, make sure that you have gone through the previous article on AVL Trees.

 

We have discussed-

  • AVL trees are self-balancing binary search trees.
  • In AVL trees, balancing factor of each node is either 0 or 1 or -1.

 

In this article, we will discuss insertion in AVL tree.

 

Insertion in AVL Tree-

 

Insertion Operation is performed to insert an element in the AVL Tree.

 

To insert an element in the AVL tree, follow the following steps-

  • Insert the element in the AVL tree in the same way the insertion is performed in BST.
  • After insertion, check the balance factor of each node of the resulting tree.

 

Read More- Insertion in Binary Search Tree

 

Now, following two cases are possible-

 

Case-01:

 

  • After the insertion, the balance factor of each node is either 0 or 1 or -1.
  • In this case, the tree is considered to be balanced.
  • Conclude the operation.
  • Insert the next element if any.

 

Case-02:

 

  • After the insertion, the balance factor of at least one node is not 0 or 1 or -1.
  • In this case, the tree is considered to be imbalanced.
  • Perform the suitable rotation to balance the tree.
  • After the tree is balanced, insert the next element if any.

 

Also Read- AVL Tree Properties

 

Rules To Remember-

 

Rule-01:

 

After inserting an element in the existing AVL tree,

  • Balance factor of only those nodes will be affected that lies on the path from the newly inserted node to the root node.

 

Rule-02:

 

To check whether the AVL tree is still balanced or not after the insertion,

  • There is no need to check the balance factor of every node.
  • Check the balance factor of only those nodes that lies on the path from the newly inserted node to the root node.

 

Rule-03:

 

After inserting an element in the AVL tree,

  • If tree becomes imbalanced, then there exists one particular node in the tree by balancing which the entire tree becomes balanced automatically.
  • To re balance the tree, balance that particular node.

 

To find that particular node,

  • Traverse the path from the newly inserted node to the root node.
  • Check the balance factor of each node that is encountered while traversing the path.
  • The first encountered imbalanced node will be the node that needs to be balanced.

 

To balance that node,

  • Count three nodes in the direction of leaf node.
  • Then, use the concept of AVL tree rotations to re balance the tree.

 

PRACTICE PROBLEM BASED ON AVL TREE INSERTION-

 

Problem-

 

Construct AVL Tree for the following sequence of numbers-

50 , 20 , 60 , 10 , 8 , 15 , 32 , 46 , 11 , 48

 

Solution-

 

Step-01: Insert 50

 

 

Step-02: Insert 20

 

  • As 20 < 50, so insert 20 in 50’s left sub tree.

 

 

Step-03: Insert 60

 

  • As 60 > 50, so insert 60 in 50’s right sub tree.

 

 

Step-04: Insert 10

 

  • As 10 < 50, so insert 10 in 50’s left sub tree.
  • As 10 < 20, so insert 10 in 20’s left sub tree.

 

 

Step-05: Insert 8

 

  • As 8 < 50, so insert 8 in 50’s left sub tree.
  • As 8 < 20, so insert 8 in 20’s left sub tree.
  • As 8 < 10, so insert 8 in 10’s left sub tree.

 

 

To balance the tree,

  • Find the first imbalanced node on the path from the newly inserted node (node 8) to the root node.
  • The first imbalanced node is node 20.
  • Now, count three nodes from node 20 in the direction of leaf node.
  • Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

Step-06: Insert 15

 

  • As 15 < 50, so insert 15 in 50’s left sub tree.
  • As 15 > 10, so insert 15 in 10’s right sub tree.
  • As 15 < 20, so insert 15 in 20’s left sub tree.

 

 

To balance the tree,

  • Find the first imbalanced node on the path from the newly inserted node (node 15) to the root node.
  • The first imbalanced node is node 50.
  • Now, count three nodes from node 50 in the direction of leaf node.
  • Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

Step-07: Insert 32

 

  • As 32 > 20, so insert 32 in 20’s right sub tree.
  • As 32 < 50, so insert 32 in 50’s left sub tree.

 

 

Step-08: Insert 46

 

  • As 46 > 20, so insert 46 in 20’s right sub tree.
  • As 46 < 50, so insert 46 in 50’s left sub tree.
  • As 46 > 32, so insert 46 in 32’s right sub tree.

 

 

Step-09: Insert 11

 

  • As 11 < 20, so insert 11 in 20’s left sub tree.
  • As 11 > 10, so insert 11 in 10’s right sub tree.
  • As 11 < 15, so insert 11 in 15’s left sub tree.

 

 

Step-10: Insert 48

 

  • As 48 > 20, so insert 48 in 20’s right sub tree.
  • As 48 < 50, so insert 48 in 50’s left sub tree.
  • As 48 > 32, so insert 48 in 32’s right sub tree.
  • As 48 > 46, so insert 48 in 46’s right sub tree.

 

 

To balance the tree,

  • Find the first imbalanced node on the path from the newly inserted node (node 48) to the root node.
  • The first imbalanced node is node 32.
  • Now, count three nodes from node 32 in the direction of leaf node.
  • Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

This is the final balanced AVL tree after inserting all the given elements.

 

To gain better understanding of AVL Tree Insertion,

Watch this Video Lecture

 

Next Article- Heap Data Structure

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Time Complexity of Binary Search Tree

Data Structures

Binary Search Tree-

 

Before you go through this article, make sure that you have gone through the previous article on BST Operations.

 

Commonly performed operations on binary search tree are-

 

 

  1. Search Operation
  2. Insertion Operation
  3. Deletion Operation

 

In this article, we will discuss time complexity of BST Operations.

 

Time Complexity-

 

  • Time complexity of all BST Operations = O(h).
  • Here, h = Height of binary search tree

 

Now, let us discuss the worst case and best case.

 

Worst Case-

 

In worst case,

  • The binary search tree is a skewed binary search tree.
  • Height of the binary search tree becomes n.
  • So, Time complexity of BST Operations = O(n).

 

In this case, binary search tree is as good as unordered list with no benefits.

 

 

Best Case-

 

In best case,

  • The binary search tree is a balanced binary search tree.
  • Height of the binary search tree becomes log(n).
  • So, Time complexity of BST Operations = O(logn).

 

 

To gain better understanding about Time Complexity of BST Operations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Introduction to AVL Trees

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.