Stop and Wait Protocol-
Before you go through this article, make sure that you have gone through the previous article on Stop and Wait Protocol.
We have discussed-
- Stop and wait protocol is a simplest flow control protocol.
- Sender sends a data packet to the receiver and then waits for its acknowledgement.
- On receiving the acknowledgement, sender sends the next data packet.
Also Read- Stop and Wait ARQ
In this article, we will discuss practice problems based on stop and wait protocol.
PRACTICE PROBLEMS BASED ON STOP AND WAIT PROTOCOL-
Problem-01:
If the bandwidth of the line is 1.5 Mbps, RTT is 45 msec and packet size is 1 KB, then find the link utilization in stop and wait.
Solution-
Given-
- Bandwidth = 1.5 Mbps
- RTT = 45 msec
- Packet size = 1 KB
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= 1 KB / 1.5 Mbps
= (210 x 8 bits) / (1.5 x 106 bits per sec)
= 5.461 msec
Calculating Propagation Delay-
Propagation delay (Tp)
= Round Trip Time / 2
= 45 msec / 2
= 22.5 msec
Calculating Value Of ‘a’-
a = Tp / Tt
a = 22.5 msec / 5.461 msec
a = 4.12
Calculating Link Utilization-
Link Utilization or Efficiency (η)
= 1 / 1+2a
= 1 / (1 + 2 x 4.12)
= 1 / 9.24
= 0.108
= 10.8 %
Problem-02:
A channel has a bit rate of 4 Kbps and one way propagation delay of 20 msec. The channel uses stop and wait protocol. The transmission time of the acknowledgement frame is negligible. To get a channel efficiency of at least 50%, the minimum frame size should be-
- 80 bytes
- 80 bits
- 160 bytes
- 160 bits
Solution-
Given-
- Bandwidth = 4 Kbps
- Propagation delay (Tp) = 20 msec
- Efficiency >= 50%
Let the required frame size = L bits.
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= L bits / 4 Kbps
Calculating Value Of ‘a’-
a = Tp / Tt
a = 20 msec / ( L bits / 4 Kbps)
a = (20 msec x 4 Kbps) / L bits
Condition For Efficiency To Be At least 50%-
For efficiency to be at least 50%, we must have-
1 / 1+2a >= 1/2
a <= 1/2
Substituting the value of ‘a’, we get-
(20 msec x 4 Kbps) / L bits <= 1/2
L bits >= (20 msec x 4 Kbps) x 2
L bits >= (20 x 10-3 sec x 4 x 103 bits per sec) x 2
L bits >= 20 x 4 bits x 2
L >= 160
From here, frame size must be at least 160 bits.
Thus, Correct Option is (D).
Problem-03:
What is the throughput achievable in stop and wait protocol by a maximum packet size of 1000 bytes and network span of 10 km.
Assume the speed of light in cable is 70% of the speed of light in vaccum.
Solution-
We have-
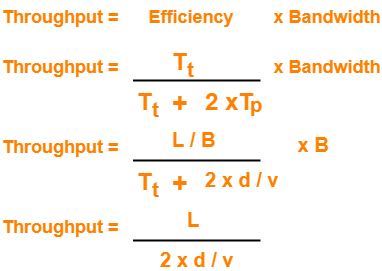
- In the given question, we are not provided with the network’s bandwidth.
- So, in the above formula of throughput, we have ignored the term Tt from the denominator.
- Although it is incorrect, but we still ignore it for solving the question.
Now, Given-
- L = 1000 bytes
- d = 10 km = 104 m
- v = 70% of 3 x 108 m/sec = 2.1 x 108 m/sec
Substituting the values in the above relation, we get-
Throughput
= 1000 bytes / [ 2 x 104 m / (2.1 x 108 m/sec)]
= 1.05 x 107 bytes per sec
= 10.5 MBps
Problem-04:
If the packet size is 1 KB and propagation time is 15 msec, the channel capacity is 109 b/sec, then find the transmission time and utilization of sender in stop and wait protocol.
Solution-
Given-
- Packet size = 1 KB
- Propagation time (Tp) = 15 msec
- Channel capacity = Bandwidth (here) = 109 b/sec
NOTE-
- Generally, channel capacity is the total number of bits which a channel can hold. So, its unit is bits.
- But here, channel capacity is actually given as bandwidth because its unit is b/sec.
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= 1 KB / 109 bits per sec
= 210 bits / 109 bits per sec
= 1.024 μsec
Calculating Value Of ‘a’-
a = Tp / Tt
a = 15 msec / 1.024 μsec
a = 15000 μsec / 1.024 μsec
a = 14648.46
Calculating Sender Utilization-
Sender Utilization or Efficiency (η)
= 1 / 1+2a
= 1 / (1 + 2 x 1468.46)
= 1 / 29297.92
= 0.0000341
= 0.00341 %
Problem-05:
Consider a MAN with average source and destination 20 Km apart and one way delay of 100 μsec. At what data rate does the round trip delay equals the transmission delay for a 1 KB packet?
Solution-
Given-
- Distance = 20 Km
- Propagation delay (Tp) = 100 μsec
- Packet size = 1 KB
We need to have-
Round Trip Time = Transmission delay
2 x Propagation delay = Transmission delay
Substituting the values in the above relation, we get-
2 x 100 μsec = 1 KB / Bandwidth
Bandwidth = 1 KB / 200 μsec
Bandwidth = (210 x 106 / 200 ) bytes per sec
Bandwidth = 5.12 MBps or 40.96 Mbps
Problem-06:
Consider two hosts X and Y connected by a single direct link of rate 106 bits/sec. The distance between the two hosts is 10,000 km and the propagation speed along the link is 2 x 108 m/sec. Host X sends a file of 50,000 bytes as one large message to host Y continuously. Let the transmission and propagation delays be p milliseconds and q milliseconds respectively.
Then the value of p and q are-
- p = 50 and q = 100
- p = 50 and q = 400
- p = 100 and q = 50
- p = 400 and q = 50
Solution-
Given-
- Bandwidth = 106 bits/sec
- Distance = 10,000 km
- Propagation speed = 2 x 108 m/sec
- Packet size = 50,000 bytes
Calculating Transmission Delay-
Transmission delay (Tt)
= Packet size / Bandwidth
= 50000 bytes / 106 bits per sec
= (5 x 104 x 8 bits) / 106 bits per sec
= ( 4 x 105 bits ) / 106 bits per sec
= 0.4 sec
= 400 msec
Calculating Propagation Delay-
Propagation delay (Tp)
= Distance / Propagation speed
= 10000 km / (2 x 108 m/sec)
= 107 m / (2 x 108 m/sec)
= 50 msec
Thus, Option (D) is correct.
Problem-07:
The values of parameters for the stop and wait ARQ protocol are as given below-
- Bit rate of the transmission channel = 1 Mbps
- Propagation delay from sender to receiver = 0.75 ms
- Time to process a frame = 0.25 ms
- Number of bytes in the information frame = 1980
- Number of bytes in the acknowledge frame = 20
- Number of overhead bytes in the information frame = 20
Assume that there are no transmission errors. Then the transmission efficiency (in %) of the stop and wait ARQ protocol for the above parameters is ___________ . (correct to 2 decimal places)
Solution-
Given-
- Bandwidth = 1 Mbps
- Propagation delay (Tp) = 0.75 ms
- Processing time (Tprocess) = 0.25 ms
- Data frame size = 1980 bytes
- Acknowledgement frame size = 20 bytes
- Overhead in data frame = 20 bytes
Calculating Useful Time-
Useful data sent
= Transmission delay of useful data bytes sent
= Useful data bytes sent / Bandwidth
= (1980 bytes – 20 bytes) / 1 Mbps
= 1960 bytes / 1 Mbps
= (1960 x 8 bits) / (106 bits per sec)
= 15680 μsec
= 15.680 msec
Calculating Total Time-
Total time
= Transmission delay of data frame + Propagation delay of data frame + Processing delay of data frame + Transmission delay of acknowledgement + Propagation delay of acknowledgement
= (1980 bytes / 1 Mbps) + 0.75 msec + 0.25 msec + (20 bytes / 1 Mbps) + 0.75 msec
= 15.840 msec + 0.75 msec + 0.25 msec + 0.160 msec + 0.75 msec
= 17.75 msec
Calculating Efficiency-
Efficiency (η)
= Useful time / Total time
= 15.680 msec / 17.75 msec
= 0.8833
= 88.33%
Problem-08:
A sender uses the stop and wait ARQ protocol for reliable transmission of frames. Frames are of size 1000 bytes and the transmission rate at the sender is 80 Kbps. Size of an acknowledgement is 100 bytes and the transmission rate at the receiver is 8 Kbps. The one way propagation delay is 100 msec.
Assuming no frame is lost, the sender throughput is __________ bytes/sec.
Solution-
Given-
- Frame size = 1000 bytes
- Sender bandwidth = 80 Kbps
- Acknowledgement size = 100 bytes
- Receiver bandwidth = 8 Kbps
- Propagation delay (Tp) = 100 msec
Calculating Transmission Delay Of Data Frame-
Transmission delay (Tt)
= Frame size / Sender bandwidth
= 1000 bytes / 80 Kbps
= (1000 x 8 bits) / (80 x 103 bits per sec)
= 0.1 sec
= 100 msec
Calculating Transmission Delay Of Acknowledgement-
Transmission delay (Tt)
= Acknowledgement size / Receiver bandwidth
= 100 bytes / 8 Kbps
= (100 x 8 bits) / (8 x 103 bits per sec)
= 100 msec
Calculating Useful Time-
Useful Time
= Transmission delay of data frame
= 100 msec
Calculating Total Time-
Total Time
= Transmission delay of data frame + Propagation delay of data frame + Transmission delay of acknowledgement + Propagation delay of acknowledgement
= 100 msec + 100 msec + 100 msec + 100 msec
= 400 msec
Calculating Efficiency-
Efficiency (η)
= Useful time / Total time
= 100 msec / 400 msec
= 1 / 4
= 25%
Calculating Sender Throughput-
Sender throughput
= Efficiency (η) x Sender bandwidth
= 0.25 x 80 Kbps
= 20 Kbps
= (20 x 1000 / 8) bytes per sec
= 2500 bytes/sec
Problem-09:
Using stop and wait protocol, sender wants to transmit 10 data packets to the receiver. Out of these 10 data packets, every 4th data packet is lost. How many packets sender will have to send in total?
Solution-
Draw a time line diagram and analyze.
The packets will be sent as-
1, 2, 3, 4, 4, 5, 6, 7, 7, 8, 9, 10, 10
The lost packets are- 4, 7 and 10.
Thus, sender will have to send 13 data packets in total.
Next Article- Sliding Window Protocol
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.