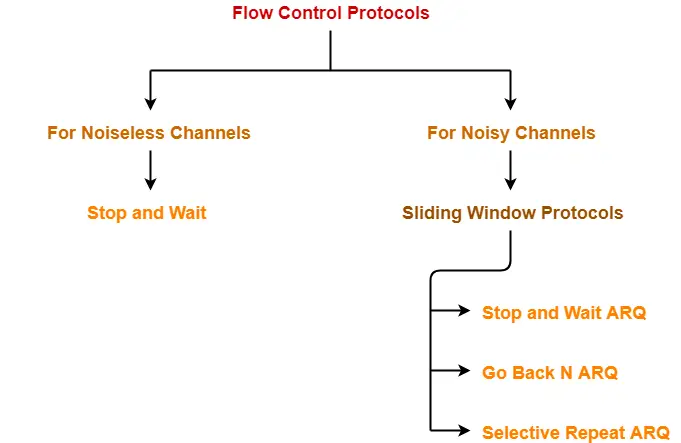
Flow Control Protocols-
In computer networking, there are various flow control protocols-
In this article, we will discuss practice problems based on these flow control protocols.
PRACTICE PROBLEMS BASED ON FLOW CONTROL PROTOCOLS-
Problem-01:
In what protocols is it possible for the sender to receive an acknowledgement for a packet that falls outside its current window?
- Stop and Wait
- Selective Repeat
- Go back N
- All of the above
Solution-
- Delayed Acknowledgements fall outside the current window.
- They may occur in any of the flow control protocols and received by the sender.
Thus, correct option is (D).
Problem-02:
On a wireless link, the probability of packet error is 0.2. A stop and wait protocol is used to transfer data across the link. The channel condition is assumed to be independent from transmission to transmission. What is the average number of transmission attempts required to transfer 100 packets?
- 100
- 125
- 150
- 200
Solution-
Method-01:
Given-
- Probability of packet error = 0.2
- We have to transfer 100 packets
Now,
- When we transfer 100 packets, number of packets in which error will occur = 0.2 x 100 = 20.
- Then, these 20 packets will have to be retransmitted.
- When we retransmit 20 packets, number of packets in which error will occur = 0.2 x 20 = 4.
- Then, these 4 packets will have to be retransmitted.
- When we retransmit 4 packets, number of packets in which error will occur = 0.2 x 4 = 0.8 ≅ 1.
- Then, this 1 packet will have to be retransmitted.
From here, average number of transmission attempts required = 100 + 20 + 4 + 1 = 125.
Thus, Option (B) is correct.
Method-02:
REMEMBERIf there are n packets to be transmitted and p is the probability of packet error, then- Number of transmission attempts required = n + np + np2 + np3 + …… + ∞ = n / (1-p) |
Substituting the given values, we get-
Average number of transmission attempts required = 100 / (1-0.2) = 125.
Thus, Option (B) is correct.
Problem-03:
Compute the fraction of the bandwidth that is wasted on overhead (headers and retransmissions) for a protocol on a heavily loaded 50 Kbps satellite channel with data frames consisting of 40 bits header and 3960 data bits. Assume that the signal propagation time from the earth to the satellite is 270 msec. ACK frames never occur. NAK frames are 40 bits. The error rate for data frames is 1% and the error rate for NAK frames is negligible.
- 1.21 %
- 2.12 %
- 1.99 %
- 1.71 %
Solution-
Consider 100 frames are being sent. Then, we have-
Useful Data Sent-
Since each frame contains 3960 data bits, so while sending 100 frames,
Useful data sent
= 100 x 3960 bits
= 396000 bits
Useless Data Sent / Overhead-
In general, overhead is due to headers, retransmissions and negative acknowledgements.
Now,
- The error rate for data frames is 1%, therefore out of 100 sent frames, error occurs in one frame.
- This causes the negative acknowledgement to follow which causes the retransmission.
So, we have-
- Overhead due to headers = 100 x 40 bits = 400 bits.
- Overhead due to negative acknowledgement = 40 bits.
- Overhead due to retransmission = 40 bits header + 3960 data bits = 4000 bits.
From here,
Total overhead
= 400 bits + 40 bits + 4000 bits
= 8040 bits
Calculating Efficiency-
Efficiency (η) = Useful data sent / Total data sent
Here,
- Useful data sent = 396000 bits
- Total data sent = Useful data sent + Overhead = 396000 bits + 8040 bits = 404040 bits
Substituting the values, we get-
Efficiency (η)
= 396000 bits / 404040 bits
= 0.9801
Calculating Bandwidth Utilization-
Bandwidth Utilization
= Efficiency x Bandwidth
= 0.9801 x 50 Kbps
= 49.005 Kbps
Calculating Bandwidth Wasted-
Bandwidth wasted
= Bandwidth – Bandwidth Utilization
= 50 Kbps – 49.005 Kbps
= 0.995 Kbps
Calculating Fraction of Bandwidth Wasted-
Fraction of bandwidth wasted
= Wasted Bandwidth / Total Available Bandwidth
= 0.995 Kbps / 50 Kbps
= 0.0199
= 1.99 %
Thus, Option (C) is correct.
Problem-04:
Consider 1 Mbps error free line. The maximum frame size is 1000 bits. New packets are generated about 1 sec apart. The time out interval is 10 msec. If the ack timer is eliminated. How many times the average message be transmitted?
- Only once
- Twice
- Thrice
- Can’t say
Solution-
- Transmission delay (Tt) = L / B = 1000 bits / 106 bits per sec = 1 msec.
- After packet is put on the link, the time out timer is started which is 10 msec long.
- The next packet is transmitted after 1 sec = 1000 msec.
- If no acknowledgement is received within 10 msec, the packet will be retransmitted.
- We have been asked how many times the average message be transmitted i.e. how many retransmissions are possible.
- Retransmission occurs or not depends on the propagation delay (Tp).
- If Tp is more, time out will occur and retransmission will take place but if Tp is less, then there will be no time out.
- Since propagation delay (Tp) is not given in the question, therefore we can not say anything.
Thus, Option (D) is correct.
Problem-05:
What is the effect on line utilization if we increase the number of frames for a constant message size?
- Lower line efficiency
- Higher line efficiency
- No change in line efficiency
- No relation between line efficiency and frame size
Solution-
In both the following cases, line utilization remains the same-
- Whether the entire message is sent as a single entity
- Or the entire message is divided into frames and then frames are sent.
This is because line contains the same amount of data in both cases.
So,
- If the number of frames are increased by dividing the message, there is no change in line efficiency.
- The line efficiency remains the same.
Thus, Option (C) is correct.
Next Article- Flow Control Methods | Single Parity Check
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.