Compiler Design | Gate Vidyalay

Category: Compiler Design

Syntax Trees | Abstract Syntax Trees

Compiler Design

Syntax Trees-

Syntax trees are abstract or compact representation of parse trees.

They are also called as Abstract Syntax Trees.

Example-

Also Read- Parse Trees

Parse Trees Vs Syntax Trees-

Parse Tree	Syntax Tree
Parse tree is a graphical representation of the replacement process in a derivation.	Syntax tree is the compact form of a parse tree.
Each interior node represents a grammar rule. Each leaf node represents a terminal.	Each interior node represents an operator. Each leaf node represents an operand.
Parse trees provide every characteristic information from the real syntax.	Syntax trees do not provide every characteristic information from the real syntax.
Parse trees are comparatively less dense than syntax trees.	Syntax trees are comparatively more dense than parse trees.

NOTE-

Syntax trees are called as Abstract Syntax Trees because-

They are abstract representation of the parse trees.
They do not provide every characteristic information from the real syntax.
For example- no rule nodes, no parenthesis etc.

PRACTICE PROBLEMS BASED ON SYNTAX TREES-

Problem-01:

Considering the following grammar-

E → E + T | T

T → T x F | F

F → ( E ) | id

Generate the following for the string id + id x id

Parse tree
Syntax tree
Directed Acyclic Graph (DAG)

Solution-

Parse Tree-

Syntax Tree-

Directed Acyclic Graph-

Also Read- Directed Acyclic Graphs

Problem-02:

Construct a syntax tree for the following arithmetic expression-

( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ))

Solution-

Step-01:

We convert the given arithmetic expression into a postfix expression as-

( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ) )

ab+ * ( c – d ) + ( ( e / f ) * ( a + b ) )

ab+ * cd- + ( ( e / f ) * ( a + b ) )

ab+ * cd- + ( ef/ * ( a + b ) )

ab+ * cd- + ( ef/ * ab+ )

ab+ * cd- + ef/ab+*

ab+cd-* + ef/ab+*

ab+cd-*ef/ab+*+

Step-02:

We draw a syntax tree for the above postfix expression.

Steps Involved

Start pushing the symbols of the postfix expression into the stack one by one.

When an operand is encountered,

Push it into the stack.

When an operator is encountered

Push it into the stack.
Pop the operator and the two symbols below it from the stack.
Perform the operation on the two operands using the operator you have in hand.
Push the result back into the stack.

Continue in the similar manner and draw the syntax tree simultaneously.

The required syntax tree is-

To gain better understanding about Syntax Trees,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Shift Reduce Parsing

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Operator Precedence Parsing

Compiler Design

Operator Precedence Grammar-

A grammar that satisfies the following 2 conditions is called as Operator Precedence Grammar–

There exists no production rule which contains ε on its RHS.
There exists no production rule which contains two non-terminals adjacent to each other on its RHS.

It represents a small class of grammar.
But it is an important class because of its widespread applications.

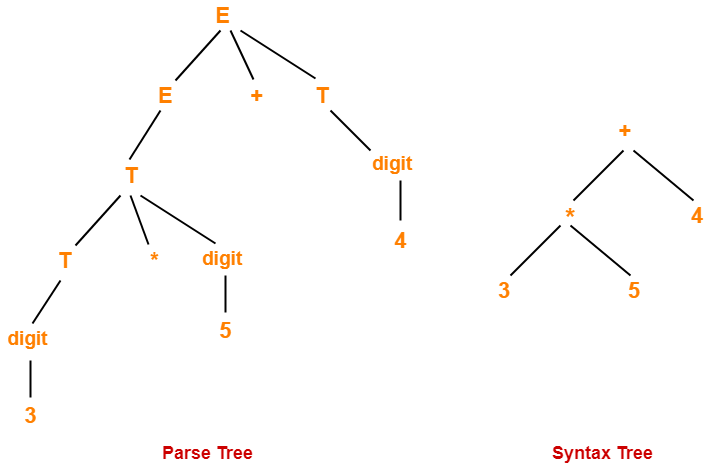
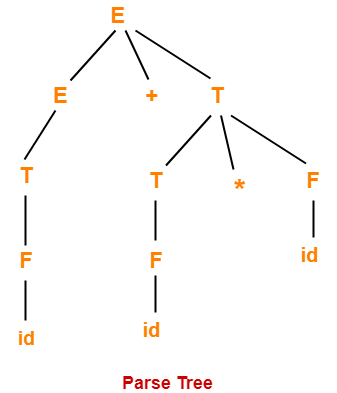
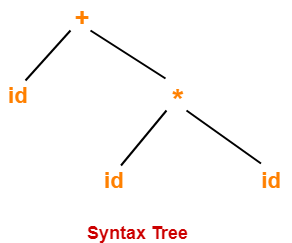
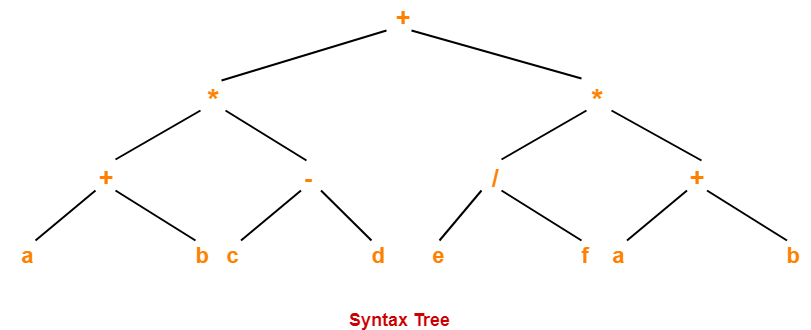
Examples-

Operator Precedence Parser-

A parser that reads and understand an operator precedence grammar

is called as Operator Precedence Parser.

Designing Operator Precedence Parser-

In operator precedence parsing,

Firstly, we define precedence relations between every pair of terminal symbols.
Secondly, we construct an operator precedence table.

Defining Precedence Relations-

The precedence relations are defined using the following rules-

Rule-01:

If precedence of b is higher than precedence of a, then we define a < b
If precedence of b is same as precedence of a, then we define a = b
If precedence of b is lower than precedence of a, then we define a > b

Rule-02:

An identifier is always given the higher precedence than any other symbol.
$ symbol is always given the lowest precedence.

Rule-03:

If two operators have the same precedence, then we go by checking their associativity.

Parsing A Given String-

The given input string is parsed using the following steps-

Step-01:

Insert the following-

$ symbol at the beginning and ending of the input string.
Precedence operator between every two symbols of the string by referring the operator precedence table.

Step-02:

Start scanning the string from LHS in the forward direction until > symbol is encountered.
Keep a pointer on that location.

Step-03:

Start scanning the string from RHS in the backward direction until < symbol is encountered.
Keep a pointer on that location.

Step-04:

Everything that lies in the middle of < and > forms the handle.
Replace the handle with the head of the respective production.

Step-05:

Keep repeating the cycle from Step-02 to Step-04 until the start symbol is reached.

Advantages-

The advantages of operator precedence parsing are-

The implementation is very easy and simple.
The parser is quite powerful for expressions in programming languages.

Disadvantages-

The disadvantages of operator precedence parsing are-

The handling of tokens known to have two different precedence becomes difficult.
Only small class of grammars can be parsed using this parser.

Important Note-

In practice, operator precedence table is not stored by the operator precedence parsers.
This is because it occupies the large space.
Instead, operator precedence parsers are implemented in a very unique style.
They are implemented using operator precedence functions.

Operator Precedence Functions-

Precedence functions perform the mapping of terminal symbols to the integers.

To decide the precedence relation between symbols, a numerical comparison is performed.
It reduces the space complexity to a large extent.

Also Read- Shift Reduce Parsing

PRACTICE PROBLEMS BASED ON OPERATOR PRECEDENCE PARSING-

Problem-01:

Consider the following grammar-

E → EAE | id

A → + | x

Construct the operator precedence parser and parse the string id + id x id.

Solution-

Step-01:

We convert the given grammar into operator precedence grammar.

The equivalent operator precedence grammar is-

E → E + E | E x E | id

Step-02:

The terminal symbols in the grammar are { id, + , x , $ }

We construct the operator precedence table as-

	id	+	x	$
id		>	>	>
+	<	>	<	>
x	<	>	>	>
$	<	<	<

Operator Precedence Table

Parsing Given String-

Given string to be parsed is id + id x id.

We follow the following steps to parse the given string-

Step-01:

We insert $ symbol at both ends of the string as-

$ id + id x id $

We insert precedence operators between the string symbols as-

$ < id > + < id > x < id > $

Step-02:

We scan and parse the string as-

$ < id > + < id > x < id > $

$ E + < id > x < id > $

$ E + E x < id > $

$ E + E x E $

$ + x $

$ < + < x > $

$ < + > $

$ $

Problem-02:

Consider the following grammar-

S → ( L ) | a

L → L , S | S

Construct the operator precedence parser and parse the string ( a , ( a , a ) ).

Solution-

The terminal symbols in the grammar are { ( , ) , a , , }

We construct the operator precedence table as-

	a	(	)	,	$
a		>	>	>	>
(	<	>	>	>	>
)	<	>	>	>	>
,	<	<	>	>	>
$	<	<	<	<

Operator Precedence Table

Parsing Given String-

Given string to be parsed is ( a , ( a , a ) ).

We follow the following steps to parse the given string-

Step-01:

We insert $ symbol at both ends of the string as-

$ ( a , ( a , a ) ) $

We insert precedence operators between the string symbols as-

$ < ( < a > , < ( < a > , < a > ) > ) > $

Step-02:

We scan and parse the string as-

$ < ( < a > , < ( < a > , < a > ) > ) > $

$ < ( S , < ( < a > , < a > ) > ) > $

$ < ( S , < ( S , < a > ) > ) > $

$ < ( S , < ( S , S ) > ) > $

$ < ( S , < ( L , S ) > ) > $

$ < ( S , < ( L ) > ) > $

$ < ( S , S ) > $

$ < ( L , S ) > $

$ < ( L ) > $

$ < S > $

$ $

Problem-03:

Consider the following grammar-

E → E + E | E x E | id

Construct Operator Precedence Parser.
Find the Operator Precedence Functions.

Solution-

The terminal symbols in the grammar are { + , x , id , $ }

We construct the operator precedence table as-

g →
f ↓		id	+	x	$
	id		>	>	>
	+	<	>	<	>
	x	<	>	>	>
	$	<	<	<

Operator Precedence Table

The graph representing the precedence functions is-

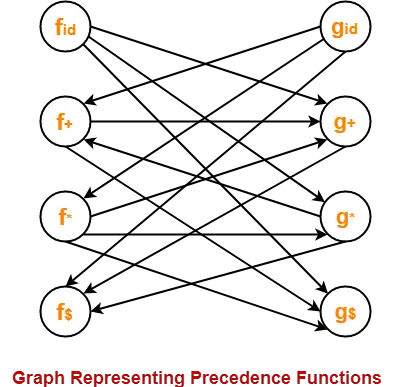
Here, the longest paths are-

f_id→ g_x → f₊ → g₊ → f_$
g_id→ f_x → g_x → f₊ → g₊ → f_$

The resulting precedence functions are-

	+	x	id	$
f	2	4	4	0
g	1	3	5	0

To gain better understanding about Operator Precedence Parsing,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Three Address Code

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Quadruples, Triples and Indirect Triples

Compiler Design

Three Address Code-

Before you go through this article, make sure that you have gone through the previous article on Three Address Code.

We have discussed-

Three Address Code is a form of an intermediate code.
It is generated by the compiler for implementing Code Optimization.
It uses maximum three addresses to represent any statement.

In this article, we will discuss Implementation of Three Address Code.

Implementation-

Three Address Code is implemented as a record with the address fields.

The commonly used representations for implementing Three Address Code are-

Quadruples
Triples
Indirect Triples

1. Quadruples-

In quadruples representation, each instruction is splitted into the following 4 different fields-

op, arg1, arg2, result

Here-

The op field is used for storing the internal code of the operator.
The arg1 and arg2 fields are used for storing the two operands used.
The result field is used for storing the result of the expression.

Exceptions

There are following exceptions-

Exception-01:

To represent the statement x = op y, we place-

op in the operator field
y in the arg1 field
x in the result field
arg2 field remains unused

Exception-02:

To represent the statement like param t1, we place-

param in the operator field
t1 in the arg1 field
Neither arg2 field nor result field is used

Exception-03:

To represent the unconditional and conditional jump statements, we place label of the target in the result field.

2. Triples-

In triples representation,

References to the instructions are made.
Temporary variables are not used.

3. Indirect Triples-

This representation is an enhancement over triples representation.
It uses an additional instruction array to list the pointers to the triples in the desired order.
Thus, instead of position, pointers are used to store the results.
It allows the optimizers to easily re-position the sub-expression for producing the optimized code.

PRACTICE PROBLEMS BASED ON QUADRUPLES, TRIPLES & INDIRECT TRIPLES-

Problem-01:

Translate the following expression to quadruple, triple and indirect triple-

a + b x c / e ↑ f + b x c

Solution-

Three Address Code for the given expression is-

T1 = e ↑ f

T2 = b x c

T3 = T2 / T1

T4 = b x a

T5 = a + T3

T6 = T5 + T4

Now, we write the required representations-

Quadruple Representation-

Location	Op	Arg1	Arg2	Result
(0)	↑	e	f	T1
(1)	x	b	c	T2
(2)	/	T2	T1	T3
(3)	x	b	a	T4
(4)	+	a	T3	T5
(5)	+	T5	T4	T6

Triple Representation-

Location	Op	Arg1	Arg2
(0)	↑	e	f
(1)	x	b	c
(2)	/	(1)	(0)
(3)	x	b	a
(4)	+	a	(2)
(5)	+	(4)	(3)

Indirect Triple Representation-

	Statement
35	(0)
36	(1)
37	(2)
38	(3)
39	(4)
40	(5)

Location	Op	Arg1	Arg2
(0)	↑	e	f
(1)	x	b	e
(2)	/	(1)	(0)
(3)	x	b	a
(4)	+	a	(2)
(5)	+	(4)	(3)

Problem-02:

Translate the following expression to quadruple, triple and indirect triple-

a = b x – c + b x – c

Solution-

Three Address Code for the given expression is-

T1 = uminus c

T2 = b x T1

T3 = uminus c

T4 = b x T3

T5 = T2 + T4

a = T5

Now, we write the required representations-

Quadruple Representation-

Location	Op	Arg1	Arg2	Result
(1)	uminus	c		T1
(2)	x	b	T1	T2
(3)	uminus	c		T3
(4)	x	b	T3	T4
(5)	+	T2	T4	T5
(6)	=	T5		a

Triple Representation-

Location	Op	Arg1	Arg2
(1)	uminus	c
(2)	x	b	(1)
(3)	uminus	c
(4)	x	b	(3)
(5)	+	(2)	(4)
(6)	=	a	(5)

Indirect Triple Representation-

	Statement
35	(1)
36	(2)
37	(3)
38	(4)
39	(5)
40	(6)

Location	Op	Arg1	Arg2
(1)	uminus	c
(2)	x	b	(1)
(3)	uminus	c
(4)	x	b	(3)
(5)	+	(2)	(4)
(6)	=	a	(5)

To gain better understanding about Quadruples, Triples and Indirect Triples,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Basic Blocks and Flow Graphs

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Code Optimization | Code Optimization Techniques

Compiler Design

Code Optimization-

Code Optimization is an approach to enhance the performance of the code.

The process of code optimization involves-

Eliminating the unwanted code lines
Rearranging the statements of the code

Advantages-

The optimized code has the following advantages-

Optimized code has faster execution speed.
Optimized code utilizes the memory efficiently.
Optimized code gives better performance.

Code Optimization Techniques-

Important code optimization techniques are-

Compile Time Evaluation
Common sub-expression elimination
Dead Code Elimination
Code Movement
Strength Reduction

1. Compile Time Evaluation-

Two techniques that falls under compile time evaluation are-

A) Constant Folding-

In this technique,

As the name suggests, it involves folding the constants.
The expressions that contain the operands having constant values at compile time are evaluated.
Those expressions are then replaced with their respective results.

Example-

Circumference of Circle = (22/7) x Diameter

Here,

This technique evaluates the expression 22/7 at compile time.
The expression is then replaced with its result 3.14.
This saves the time at run time.

B) Constant Propagation-

In this technique,

If some variable has been assigned some constant value, then it replaces that variable with its constant value in the further program during compilation.
The condition is that the value of variable must not get alter in between.

Example-

pi = 3.14

radius = 10

Area of circle = pi x radius x radius

Here,

This technique substitutes the value of variables ‘pi’ and ‘radius’ at compile time.
It then evaluates the expression 3.14 x 10 x 10.
The expression is then replaced with its result 314.
This saves the time at run time.

2. Common Sub-Expression Elimination-

The expression that has been already computed before and appears again in the code for computation

is called as Common Sub-Expression.

In this technique,

As the name suggests, it involves eliminating the common sub expressions.
The redundant expressions are eliminated to avoid their re-computation.
The already computed result is used in the further program when required.

Example-

Code Before Optimization

Code After Optimization

S1 = 4 x i

S2 = a[S1]

S3 = 4 x j

S4 = 4 x i // Redundant Expression

S5 = n

S6 = b[S4] + S5

S1 = 4 x i

S2 = a[S1]

S3 = 4 x j

S5 = n

S6 = b[S1] + S5

3. Code Movement-

In this technique,

As the name suggests, it involves movement of the code.
The code present inside the loop is moved out if it does not matter whether it is present inside or outside.
Such a code unnecessarily gets execute again and again with each iteration of the loop.
This leads to the wastage of time at run time.

Example-

Code Before Optimization

Code After Optimization

for ( int j = 0 ; j < n ; j ++)

{

x = y + z ;

a[j] = 6 x j;

}

x = y + z ;

for ( int j = 0 ; j < n ; j ++)

{

a[j] = 6 x j;

}

4. Dead Code Elimination-

In this technique,

As the name suggests, it involves eliminating the dead code.
The statements of the code which either never executes or are unreachable or their output is never used are eliminated.

Example-

Code Before Optimization

Code After Optimization

i = 0 ;

if (i == 1)

{

a = x + 5 ;

}

i = 0 ;

5. Strength Reduction-

In this technique,

As the name suggests, it involves reducing the strength of expressions.
This technique replaces the expensive and costly operators with the simple and cheaper ones.

Example-

Code Before Optimization	Code After Optimization
B = A x 2	B = A + A

Here,

The expression “A x 2” is replaced with the expression “A + A”.
This is because the cost of multiplication operator is higher than that of addition operator.

To gain better understanding about Code Optimization Techniques,

Watch this Video Lecture

Download Handwritten Notes Here-

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Three Address Code | Examples

Compiler Design

Three Address Code-

Three Address Code is a form of an intermediate code.

The characteristics of Three Address instructions are-

They are generated by the compiler for implementing Code Optimization.
They use maximum three addresses to represent any statement.
They are implemented as a record with the address fields.

General Form-

In general, Three Address instructions are represented as-

a = b op c

Here,

a, b and c are the operands.
Operands may be constants, names, or compiler generated temporaries.
op represents the operator.

Examples-

Examples of Three Address instructions are-

a = b + c
c = a x b

Common Three Address Instruction Forms-

The common forms of Three Address instructions are-

1. Assignment Statement-

x = y op z and x = op y

Here,

x, y and z are the operands.
op represents the operator.

It assigns the result obtained after solving the right side expression of the assignment operator to the left side operand.

2. Copy Statement-

x = y

Here,

x and y are the operands.
= is an assignment operator.

It copies and assigns the value of operand y to operand x.

3. Conditional Jump-

If x relop y goto X

Here,

x & y are the operands.
X is the tag or label of the target statement.
relop is a relational operator.

If the condition “x relop y” gets satisfied, then-

The control is sent directly to the location specified by label X.
All the statements in between are skipped.

If the condition “x relop y” fails, then-

The control is not sent to the location specified by label X.
The next statement appearing in the usual sequence is executed.

4. Unconditional Jump-

goto X

Here, X is the tag or label of the target statement.

On executing the statement,

The control is sent directly to the location specified by label X.
All the statements in between are skipped.

5. Procedure Call-

param x call p return y

Here, p is a function which takes x as a parameter and returns y.

PRACTICE PROBLEMS BASED ON THREE ADDRESS CODE-

To solve the problems, Learn about the Precedence Relations and Associativity of Operators.

Problem-01:

Write Three Address Code for the following expression-

a = b + c + d

Solution-

The given expression will be solved as-

Three Address Code for the given expression is-

(1) T1 = b + c

(2) T2 = T1 + d

(3) a = T2

Problem-02:

Write Three Address Code for the following expression-

-(a x b) + (c + d) – (a + b + c + d)

Solution-

Three Address Code for the given expression is-

(1) T1 = a x b

(2) T2 = uminus T1

(3) T3 = c + d

(4) T4 = T2 + T3

(5) T5 = a + b

(6) T6 = T3 + T5

(7) T7 = T4 – T6

Problem-03:

Write Three Address Code for the following expression-

If A < B then 1 else 0

Solution-

Three Address Code for the given expression is-

(1) If (A < B) goto (4)

(2) T1 = 0

(3) goto (5)

(4) T1 = 1

(5)

Problem-04:

Write Three Address Code for the following expression-

If A < B and C < D then t = 1 else t = 0

Solution-

Three Address Code for the given expression is-

(1) If (A < B) goto (3)

(2) goto (4)

(3) If (C < D) goto (6)

(4) t = 0

(5) goto (7)

(6) t = 1

(7)

Also Read- More Problems On Three Address Code

To gain better understanding about Three Address Code,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Quadruples, Triples & Indirect Triples

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

← Older Posts

Newer Posts →