Compiler Design | Gate Vidyalay

First and Follow | Solved Examples

First and Follow-

First and Follow sets are needed so that the parser can properly apply the needed production rule at the correct position.

In this article, we will learn how to calculate first and follow functions.

First Function-

First(α) is a set of terminal symbols that begin in strings derived from α.

Example-

Consider the production rule-

A → abc / def / ghi

Then, we have-

First(A) = { a , d , g }

Rules For Calculating First Function-

Rule-01:

For a production rule X → ∈,

First(X) = { ∈ }

Rule-02:

For any terminal symbol ‘a’,

First(a) = { a }

Rule-03:

For a production rule X → Y₁Y₂Y₃,

Calculating First(X)

If ∈ ∉ First(Y₁), then First(X) = First(Y₁)
If ∈ ∈ First(Y₁), then First(X) = { First(Y₁) – ∈ } ∪ First(Y₂Y₃)

Calculating First(Y₂Y₃)

If ∈ ∉ First(Y₂), then First(Y₂Y₃) = First(Y₂)
If ∈ ∈ First(Y₂), then First(Y₂Y₃) = { First(Y₂) – ∈ } ∪ First(Y₃)

Similarly, we can make expansion for any production rule X → Y₁Y₂Y₃…..Y_n.

Follow Function-

Follow(α) is a set of terminal symbols that appear immediately to the right of α.

Rules For Calculating Follow Function-

Rule-01:

For the start symbol S, place $ in Follow(S).

Rule-02:

For any production rule A → αB,

Follow(B) = Follow(A)

Rule-03:

For any production rule A → αBβ,

If ∈ ∉ First(β), then Follow(B) = First(β)
If ∈ ∈ First(β), then Follow(B) = { First(β) – ∈ } ∪ Follow(A)

Important Notes-

Note-01:

∈ may appear in the first function of a non-terminal.
∈ will never appear in the follow function of a non-terminal.

Note-02:

Before calculating the first and follow functions, eliminate Left Recursion from the grammar, if present.

Note-03:

We calculate the follow function of a non-terminal by looking where it is present on the RHS of a production rule.

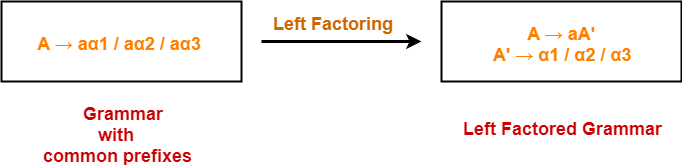
Also Read- Left Factoring

PRACTICE PROBLEMS BASED ON CALCULATING FIRST AND FOLLOW-

Problem-01:

Calculate the first and follow functions for the given grammar-

S → aBDh

B → cC

C → bC / ∈

D → EF

E → g / ∈

F → f / ∈

Solution-

The first and follow functions are as follows-

First Functions-

First(S) = { a }
First(B) = { c }
First(C) = { b , ∈ }
First(D) = { First(E) – ∈ } ∪ First(F) = { g , f , ∈ }
First(E) = { g , ∈ }
First(F) = { f , ∈ }

Follow Functions-

Follow(S) = { $ }
Follow(B) = { First(D) – ∈ } ∪ First(h) = { g , f , h }
Follow(C) = Follow(B) = { g , f , h }
Follow(D) = First(h) = { h }
Follow(E) = { First(F) – ∈ } ∪ Follow(D) = { f , h }
Follow(F) = Follow(D) = { h }

Problem-02:

Calculate the first and follow functions for the given grammar-

S → A

A → aB / Ad

B → b

C → g

Solution-

We have-

The given grammar is left recursive.
So, we first remove left recursion from the given grammar.

After eliminating left recursion, we get the following grammar-

S → A

A → aBA’

A’ → dA’ / ∈

B → b

C → g

Now, the first and follow functions are as follows-

First Functions-

First(S) = First(A) = { a }
First(A) = { a }
First(A’) = { d , ∈ }
First(B) = { b }
First(C) = { g }

Follow Functions-

Follow(S) = { $ }
Follow(A) = Follow(S) = { $ }
Follow(A’) = Follow(A) = { $ }
Follow(B) = { First(A’) – ∈ } ∪ Follow(A) = { d , $ }
Follow(C) = NA

Problem-03:

Calculate the first and follow functions for the given grammar-

S → (L) / a

L → SL’

L’ → ,SL’ / ∈

Solution-

The first and follow functions are as follows-

First Functions-

First(S) = { ( , a }
First(L) = First(S) = { ( , a }
First(L’) = { , , ∈ }

Follow Functions-

Follow(S) = { $ } ∪ { First(L’) – ∈ } ∪ Follow(L) ∪ Follow(L’) = { $ , , , ) }
Follow(L) = { ) }
Follow(L’) = Follow(L) = { ) }

Problem-04:

Calculate the first and follow functions for the given grammar-

S → AaAb / BbBa

A → ∈

B → ∈

Solution-

The first and follow functions are as follows-

First Functions-

First(S) = { First(A) – ∈ } ∪ First(a) ∪ { First(B) – ∈ } ∪ First(b) = { a , b }
First(A) = { ∈ }
First(B) = { ∈ }

Follow Functions-

Follow(S) = { $ }
Follow(A) = First(a) ∪ First(b) = { a , b }
Follow(B) = First(b) ∪ First(a) = { a , b }

Problem-05:

Calculate the first and follow functions for the given grammar-

E → E + T / T

T → T x F / F

F → (E) / id

Solution-

We have-

The given grammar is left recursive.
So, we first remove left recursion from the given grammar.

After eliminating left recursion, we get the following grammar-

E → TE’

E’ → + TE’ / ∈

T → FT’

T’ → x FT’ / ∈

F → (E) / id

Now, the first and follow functions are as follows-

First Functions-

First(E) = First(T) = First(F) = { ( , id }
First(E’) = { + , ∈ }
First(T) = First(F) = { ( , id }
First(T’) = { x , ∈ }
First(F) = { ( , id }

Follow Functions-

Follow(E) = { $ , ) }
Follow(E’) = Follow(E) = { $ , ) }
Follow(T) = { First(E’) – ∈ } ∪ Follow(E) ∪ Follow(E’) = { + , $ , ) }
Follow(T’) = Follow(T) = { + , $ , ) }
Follow(F) = { First(T’) – ∈ } ∪ Follow(T) ∪ Follow(T’) = { x , + , $ , ) }

Problem-06:

Calculate the first and follow functions for the given grammar-

S → ACB / CbB / Ba

A → da / BC

B → g / ∈

C → h / ∈

Solution-

The first and follow functions are as follows-

First Functions-

First(S) = { First(A) – ∈ } ∪ { First(C) – ∈ } ∪ First(B) ∪ First(b) ∪ { First(B) – ∈ } ∪ First(a) = { d , g , h , ∈ , b , a }
First(A) = First(d) ∪ { First(B) – ∈ } ∪ First(C) = { d , g , h , ∈ }
First(B) = { g , ∈ }
First(C) = { h , ∈ }

Follow Functions-

Follow(S) = { $ }
Follow(A) = { First(C) – ∈ } ∪ { First(B) – ∈ } ∪ Follow(S) = { h , g , $ }
Follow(B) = Follow(S) ∪ First(a) ∪ { First(C) – ∈ } ∪ Follow(A) = { $ , a , h , g }
Follow(C) = { First(B) – ∈ } ∪ Follow(S) ∪ First(b) ∪ Follow(A) = { g , $ , b , h }

To gain better understanding about calculating first and follow functions,

Watch this Video Lecture

Next Article- Syntax Trees

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Left Factoring | Left Factoring Examples

Compiler Design

Grammar With Common Prefixes-

If RHS of more than one production starts with the same symbol,

then such a grammar is called as

Grammar With Common Prefixes.

Example-

A → αβ₁ / αβ₂ / αβ₃

(Grammar with common prefixes)

This kind of grammar creates a problematic situation for Top down parsers.
Top down parsers can not decide which production must be chosen to parse the string in hand.

To remove this confusion, we use left factoring.

Left Factoring-

Left factoring is a process by which the grammar with common prefixes is transformed

to make it useful for Top down parsers.

How?

In left factoring,

We make one production for each common prefixes.
The common prefix may be a terminal or a non-terminal or a combination of both.
Rest of the derivation is added by new productions.

Again, this is a grammar with common prefixes.

Step-03:

S → aS’

S’ → bA / ∈

A → cB / ∈

B → d / ∈

This is a left factored grammar.

Problem-06:

Do left factoring in the following grammar-

S → aAd / aB

A → a / ab

B → ccd / ddc

Solution-

The left factored grammar is-

S → aS’

S’ → Ad / B

A → aA’

A’ → b / ∈

B → ccd / ddc

To gain better understanding about Left Factoring,

Watch this Video Lecture

Next Article- Relationship With Left Recursion

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Miscellaneous Problems in Compiler Design

Compiler Design

Three Address Code | DAGs | Basic Blocks & Flow Graphs-

Before you go through this article, make sure that you have gone through the previous articles on-

In this article, we will solve Miscellaneous Problems based on these Concepts.

PRACTICE PROBLEMS BASED ON ABOVE CONCEPTS-

Problem-01:

Generate three address code for the following code-

c = 0

do

{

if (a < b) then

x++;

else

x–;

c++;

} while (c < 5)

Solution-

Three address code for the given code is-

c = 0
if (a < b) goto (4)
goto (7)
T1 = x + 1
x = T1
goto (9)
T2 = x – 1
x = T2
T3 = c + 1
c = T3
if (c < 5) goto (2)

Problem-02:

Generate three address code for the following code-

while (A < C and B > D) do

if A = 1 then C = C + 1

else

while A <= D

do A = A + B

Solution-

Three address code for the given code is-

if (A < C) goto (3)
goto (15)
if (B > D) goto (5)
goto (15)
if (A = 1) goto (7)
goto (10)
T1 = c + 1
c = T1
goto (1)
if (A <= D) goto (12)
goto (1)
T2 = A + B
A = T2
goto (10)

Problem-03:

Generate three address code for the following code-

switch (ch)

{

case 1 : c = a + b;

break;

case 2 : c = a – b;

break;

}

Solution-

Three address code for the given code is-

if ch = 1 goto L1

if ch = 2 goto L2

L1:

T1 = a + b

c = T1

goto Last

L2:

T1 = a – b

c = T2

goto Last

Last:

Problem-04:

Construct a DAG for the following three address code-

a = b + c
t1 = a x a
b = t1 + a
c = t1 x b
t2 = c + b
a = t2 + t2

Solution-

Directed acyclic graph for the given three address code is-

Problem-05:

Consider the following code-

prod = 0 ;

i = 1 ;

do

{

prod = prod + a[ i ] x b[ i ] ;

i = i + 1 ;

} while (i <= 10) ;

Compute the three address code.
Compute the basic blocks and draw the flow graph.

Solution-

Part-01:

Three address code for the given code is-

prod = 0

i = 1

T1 = 4 x i

T2 = a[T1]

T3 = 4 x i

T4 = b[T3]

T5 = T2 x T4

T6 = T5 + prod

prod = T6

T7 = i + 1

i = T7

if (i <= 10) goto (3)

Part-02:

Step-01:

We identify the leader statements as-

prod = 0 is a leader because first statement is a leader.
T1 = 4 x i is a leader because target of conditional or unconditional goto is a leader.

Step-02:

The above generated three address code can be partitioned into 2 basic blocks as-

Step-03:

The flow graph is-

To gain better understanding about these Miscellaneous Problems,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Code Optimization

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Relation between Left Recursion & Left Factoring

Compiler Design

Relationship Between Left Recursion, Left Factoring & Ambiguity-

There is no relationship between Left Recursion, Left Factoring and Ambiguity of Grammar.

All the three concepts are independent and has nothing to do with each other.
The presence or absence of left recursion does not impact left factoring and ambiguity anyhow.
The presence or absence of left factoring does not impact left recursion and ambiguity anyhow.
The presence or absence of ambiguity does not impact left recursion and left factoring anyhow.

The following examples support this fact-

Example-01: Ambiguous Grammar With Left Factoring-

Consider the following grammar-

S → aS / a / ∈

Clearly, this grammar has left factoring.

Now, let us draw parse trees for the string w = a-

Clearly,

Two different parse trees exist for the string w = a.
Therefore, the grammar is ambiguous.

Example-02: Unambiguous Grammar With Left Factoring-

Consider the following grammar-

S → aA / aB

A → a

B → b

Clearly, this grammar has left factoring.

The language generated by this grammar consists of only two strings L(G) = { aa , ab}.

Now, let us draw parse trees for these strings-

Clearly,

A unique parse tree exists for both the strings.
Therefore, the grammar is unambiguous.

Example-03: Ambiguous Grammar With Left Recursion-

Consider the following grammar-

S → SS / ∈

Clearly, this grammar has left recursion.

Now, let us draw parse trees for the string w = ∈-

Clearly,

Infinite parse trees exist for the string w = ∈.
Therefore, the grammar is ambiguous.

Example-04: Unambiguous Grammar With Left Recursion-

Consider the following grammar-

S → Sa / ∈

Clearly, this grammar has left recursion.

A unique parse tree exists for all the strings that can be generated from the grammar.

Therefore, the grammar is unambiguous.

Example-05: Ambiguous Grammar Without Left Recursion & Without Left Factoring-

Consider the following grammar-

S → aA / Ba

A → a

B → a

Clearly, this grammar has neither left recursion nor left factoring.

Now, let us draw parse trees for the string w = aa-

Clearly,

Two different parse trees exist for the string w = aa.
Therefore, the grammar is ambiguous.

Example-06: Unambiguous Grammar With Both Left Recursion & Left Factoring-

Consider the following grammar-

S → Sa / ɛ / bB / bD

B → b

D → d

Clearly, this grammar has both left recursion and left factoring.

A unique parse tree exists for all the strings that can be generated from the grammar.

Therefore, the grammar is unambiguous.

To gain better understanding about relationship between left recursion, left factoring and ambiguity-

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Calculating First and Follow

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Shift Reduce Parser | Shift Reduce Parsing

Compiler Design

Shift-Reduce Parser-

A shift-reduce parser is a bottom-up parser.

It takes the given input string and builds a parse tree-

Starting from the bottom at the leaves.
And growing the tree towards the top to the root.

Data Structures-

Two data structures are required to implement a shift-reduce parser-

A Stack is required to hold the grammar symbols.
An Input buffer is required to hold the string to be parsed.

Working-

Initially, shift-reduce parser is present in the following configuration where-

Stack contains only the $ symbol.
Input buffer contains the input string with $ at its end.

The parser works by-

Moving the input symbols on the top of the stack.
Until a handle β appears on the top of the stack.

The parser keeps on repeating this cycle until-

An error is detected.
Or stack is left with only the start symbol and the input buffer becomes empty.

After achieving this configuration,

The parser stops / halts.
It reports the successful completion of parsing.

Possible Actions-

A shift-reduce parser can possibly make the following four actions-

1. Shift-

In a shift action,

The next symbol is shifted onto the top of the stack.

2. Reduce-

In a reduce action,

The handle appearing on the stack top is replaced with the appropriate non-terminal symbol.

3. Accept-

In an accept action,

The parser reports the successful completion of parsing.

4. Error-

In this state,

The parser becomes confused and is not able to make any decision.
It can neither perform shift action nor reduce action nor accept action.

Rules To Remember

It is important to remember the following rules while performing the shift-reduce action-

If the priority of incoming operator is more than the priority of in stack operator, then shift action is performed.
If the priority of in stack operator is same or less than the priority of in stack operator, then reduce action is performed.

PRACTICE PROBLEMS BASED ON SHIFT-REDUCE PARSING-

Problem-01:

Consider the following grammar-

E → E – E

E → E x E

E → id

Parse the input string id – id x id using a shift-reduce parser.

Solution-

The priority order is: id > x > –

Stack	Input Buffer	Parsing Action
$	id – id x id $	Shift
$ id	– id x id $	Reduce E → id
$ E	– id x id $	Shift
$ E –	id x id $	Shift
$ E – id	x id $	Reduce E → id
$ E – E	x id $	Shift
$ E – E x	id $	Shift
$ E – E x id	$	Reduce E → id
$ E – E x E	$	Reduce E → E x E
$ E – E	$	Reduce E → E – E
$ E	$	Accept

Problem-02:

Consider the following grammar-

S → ( L ) | a

L → L , S | S

Parse the input string ( a , ( a , a ) ) using a shift-reduce parser.

Solution-

Stack	Input Buffer	Parsing Action
$	( a , ( a , a ) ) $	Shift
$ (	a , ( a , a ) ) $	Shift
$ ( a	, ( a , a ) ) $	Reduce S → a
$ ( S	, ( a , a ) ) $	Reduce L → S
$ ( L	, ( a , a ) ) $	Shift
$ ( L ,	( a , a ) ) $	Shift
$ ( L , (	a , a ) ) $	Shift
$ ( L , ( a	, a ) ) $	Reduce S → a
$ ( L , ( S	, a ) ) $	Reduce L → S
$ ( L , ( L	, a ) ) $	Shift
$ ( L , ( L ,	a ) ) $	Shift
$ ( L , ( L , a	) ) $	Reduce S → a
$ ( L , ( L , S )	) ) $	Reduce L → L , S
$ ( L , ( L	) ) $	Shift
$ ( L , ( L )	) $	Reduce S → (L)
$ ( L , S	) $	Reduce L → L , S
$ ( L	) $	Shift
$ ( L )	$	Reduce S → (L)
$ S	$	Accept

Problem-03:

Consider the following grammar-

S → T L

T → int | float

L → L , id | id

Parse the input string int id , id ; using a shift-reduce parser.

Solution-

Stack	Input Buffer	Parsing Action
$	int id , id ; $	Shift
$ int	id , id ; $	Reduce T → int
$ T	id , id ; $	Shift
$ T id	, id ; $	Reduce L → id
$ T L	, id ; $	Shift
$ T L ,	id ; $	Shift
$ T L , id	; $	Reduce L → L , id
$ T L	; $	Shift
$ T L ;	$	Reduce S → T L
$ S	$	Accept

Problem-04:

Considering the string “10201”, design a shift-reduce parser for the following grammar-

S → 0S0 | 1S1 | 2

Solution-

Stack	Input Buffer	Parsing Action
$	1 0 2 0 1 $	Shift
$ 1	0 2 0 1 $	Shift
$ 1 0	2 0 1 $	Shift
$ 1 0 2	0 1 $	Reduce S → 2
$ 1 0 S	0 1 $	Shift
$ 1 0 S 0	1 $	Reduce S → 0 S 0
$ 1 S	1 $	Shift
$ 1 S 1	$	Reduce S → 1 S 1
$ S	$	Accept

To gain better understanding about Shift-Reduce Parsing,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Operator Precedence Parsing

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Category: Compiler Design

First and Follow-

First Function-

Example-

Rules For Calculating First Function-

Rule-01:

Rule-02:

Rule-03:

Calculating First(X)

Calculating First(Y2Y3)

Follow Function-

Rules For Calculating Follow Function-

Rule-01:

Rule-02:

Rule-03:

Important Notes-

Note-01:

Note-02:

Note-03:

PRACTICE PROBLEMS BASED ON CALCULATING FIRST AND FOLLOW-

Problem-01:

Solution-

First Functions-

Follow Functions-

Problem-02:

Solution-

First Functions-

Follow Functions-

Problem-03:

Solution-

First Functions-

Follow Functions-

Problem-04:

Solution-

First Functions-

Follow Functions-

Problem-05:

Solution-

First Functions-

Follow Functions-

Problem-06:

Solution-

First Functions-

Follow Functions-

Grammar With Common Prefixes-

Example-

Left Factoring-

How?

Example-

PRACTICE PROBLEMS BASED ON LEFT FACTORING-

Problem-01:

Solution-

Problem-02:

Solution-

Step-01:

Step-02:

Problem-03:

Solution-

Step-01:

Step-02:

Problem-04:

Solution-

Step-01:

Step-02:

Problem-05:

Solution-

Step-01:

Step-02:

Step-03:

Problem-06:

Solution-

Three Address Code | DAGs | Basic Blocks & Flow Graphs-

PRACTICE PROBLEMS BASED ON ABOVE CONCEPTS-

Problem-01:

Solution-

Problem-02:

Solution-

Problem-03:

Solution-

Problem-04:

Calculating First(Y₂Y₃)