Carry Look Ahead Adder | 4-bit Carry Look Ahead Adder

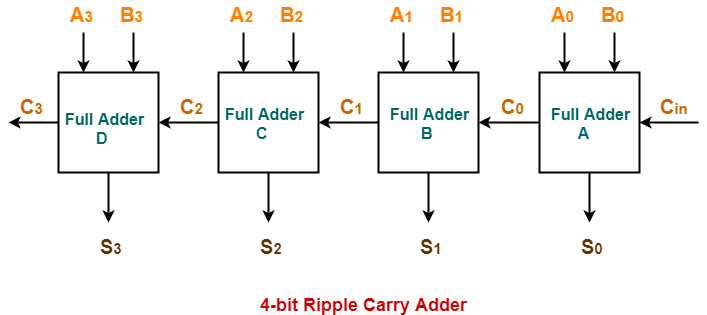
Ripple Carry Adder-

 

Before you go through this article, make sure that you have gone through the previous article on Ripple Carry Adder.

 

In Ripple Carry Adder,

• Each full adder has to wait for its carry-in from its previous stage full adder.
• Thus, n^th full adder has to wait until all (n-1) full adders have completed their operations.
• This causes a delay and makes ripple carry adder extremely slow.
• The situation becomes worst when the value of n becomes very large.
• To overcome this disadvantage, Carry Look Ahead Adder comes into play.

 

 

In this article, we will discuss about Carry Look Ahead Adder.

 

Carry Look Ahead Adder-

 

• Carry Look Ahead Adder is an improved version of the ripple carry adder.
• It generates the carry-in of each full adder simultaneously without causing any delay.
• The time complexity of carry look ahead adder = Θ (logn).

 

Logic Diagram-

 

The logic diagram for carry look ahead adder is as shown below-

 

 

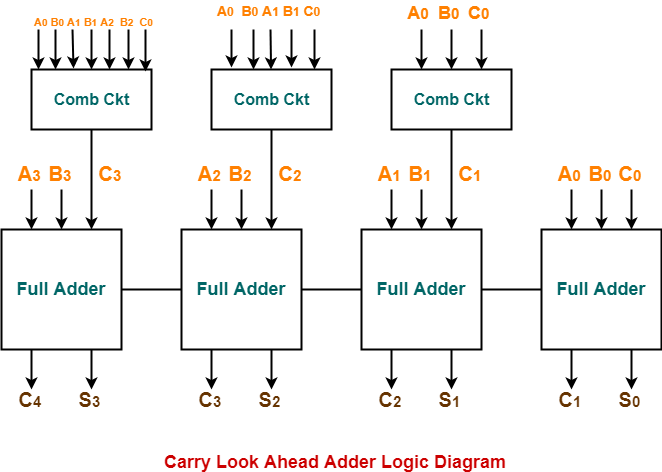
Carry Look Ahead Adder Working-

 

The working of carry look ahead adder is based on the principle- The carry-in of any stage full adder is independent of the carry bits generated during intermediate stages.

 

The carry-in of any stage full adder depends only on the following two parameters-

• Bits being added in the previous stages
• Carry-in provided in the beginning

 

Now,

• The above two parameters are always known from the beginning.
• So, the carry-in of any stage full adder can be evaluated at any instant of time.
• Thus, any full adder need not wait until its carry-in is generated by its previous stage full adder.

 

Also Read- Full Adder Working

 

4-Bit Carry Look Ahead Adder-

 

Consider two 4-bit binary numbers A₃A₂A₁A₀ and B₃B₂B₁B₀ are to be added.

Mathematically, the two numbers will be added as-

 

 

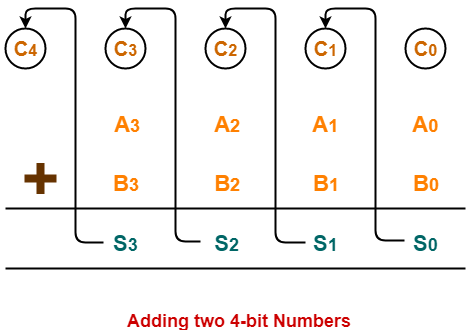
From here, we have-

C₁ = C₀ (A₀ ⊕ B₀) + A₀B₀

C₂ = C₁ (A₁ ⊕ B₁) + A₁B₁

C₃ = C₂ (A₂ ⊕ B₂) + A₂B₂

C₄ = C₃ (A₃ ⊕ B₃) + A₃B₃

 

For simplicity, Let-

• G_i = A_iB_i where G is called carry generator
• P_i = A_i ⊕ B_i where P is called carry propagator

 

Then, re-writing the above equations, we have-

C₁ = C₀P₀ + G₀ ………….. (1)

C₂ = C₁P₁ + G₁ ………….. (2)

C₃ = C₂P₂ + G₂ ………….. (3)

C₄ = C₃P₃ + G₃ ………….. (4)

 

Now,

• Clearly, C1, C2 and C3 are intermediate carry bits.
• So, let’s remove C₁, C₂ and C₃ from RHS of every equation.
• Substituting (1) in (2), we get C₂ in terms of C₀.
• Then, substituting (2) in (3), we get C₃ in terms of C₀ and so on.

 

Finally, we have the following equations-

• C₁ = C₀P₀ + G₀ 
• C₂ = C₀P₀P₁ + G₀P₁ + G₁
• C₃ = C₀P₀P₁P₂ + G₀P₁P₂ + G₁P₂ + G₂
• C₄ =C₀P₀P₁P₂P3 + G₀P₁P₂P₃ + G₁P₂P₃ + G₂P₃ + G₃

 

These equations are important to remember.

 

These equations show that the carry-in of any stage full adder depends only on-

• Bits being added in the previous stages
• Carry bit which was provided in the beginning

 

Trick To Memorize Above Equations-

 

As an example, let us consider the equation for generating carry bit C₂.

There are three possible reasons for generation of C₂ as depicted in the following picture-

 

 

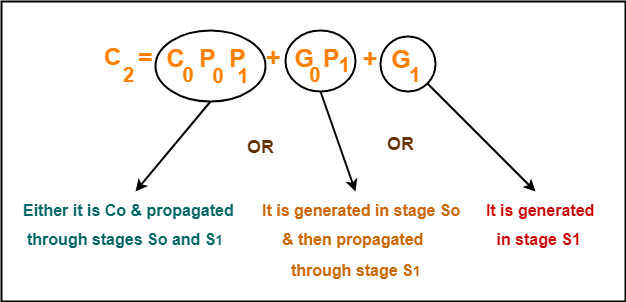
In the similar manner, we can write other equations as well very easily.

 

Implementation Of Carry Generator Circuits-

 

The above carry generator circuits are usually implemented as-

• Two level combinational circuits.
• Using AND and OR gates where gates are assumed to have any number of inputs.

 

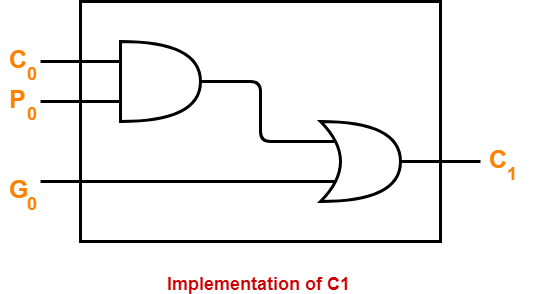
Implementation Of C₁–

 

• The carry generator circuit for C1 is implemented as shown below.
• It requires 1 AND gate and 1 OR gate.

 

C₁ = C₀P₀ + G₀

 

Implementation Of C₂–

 

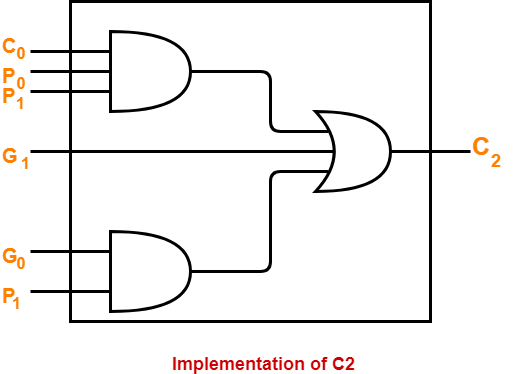
• The carry generator circuit for C2 is implemented as shown below.
• It requires 2 AND gates and 1 OR gate.

 

C₂ = C₀P₀P₁ + G₀P₁ + G₁

 

Implementation Of C₃ & C₄–

 

Similarly, we implement C₃ and C₄.

• Implementation of C₃ uses 3 AND gates and 1 OR gate.
• Implementation of C₄ uses 4 AND gates and 1 OR gate.

 

Total number of gates required to implement carry generators (provided carry propagators P_i and carry generators G_i) are-

• Total number of AND gates required for addition of 4-bit numbers = 1 + 2 + 3 + 4 = 10.
• Total number of OR gates required for addition of 4-bit numbers = 1 + 1 + 1 + 1 = 4.

 

General Formula-

 

The following formula is used to calculate number of gates required for evaluating all carry bits-

 

For a n-bit carry look ahead adder to evaluate all the carry bits, it requires- Number of AND gates = n(n+1) / 2 Number of OR gates = n

 

Advantages of Carry Look Ahead Adder-

 

The advantages of carry look ahead adder are-

• It generates the carry-in for each full adder simultaneously.
• It reduces the propagation delay.

 

Disadvantages of Carry Look Ahead Adder-

 

The disadvantages of carry look ahead adder are-

• It involves complex hardware.
• It is costlier since it involves complex hardware.
• It gets more complicated as the number of bits increases.

 

To gain better understanding about Carry Look Ahead Adder,

Watch this Video Lecture

 

Next Article- K Maps | Karnaugh Maps

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.