Line Drawing Algorithms-
In computer graphics, popular algorithms used to generate lines are-

- Digital Differential Analyzer (DDA) Line Drawing Algorithm
- Bresenham Line Drawing Algorithm
- Mid Point Line Drawing Algorithm
In this article, we will discuss about Bresenham Line Drawing Algorithm.
Bresenham Line Drawing Algorithm-
| Given the starting and ending coordinates of a line,
Bresenham Line Drawing Algorithm attempts to generate the points between the starting and ending coordinates. |
Also Read- DDA Line Drawing Algorithm
Procedure-
Given-
- Starting coordinates = (X0, Y0)
- Ending coordinates = (Xn, Yn)
The points generation using Bresenham Line Drawing Algorithm involves the following steps-
Step-01:
Calculate ΔX and ΔY from the given input.
These parameters are calculated as-
- ΔX = Xn – X0
- ΔY =Yn – Y0
Step-02:
Calculate the decision parameter Pk.
It is calculated as-
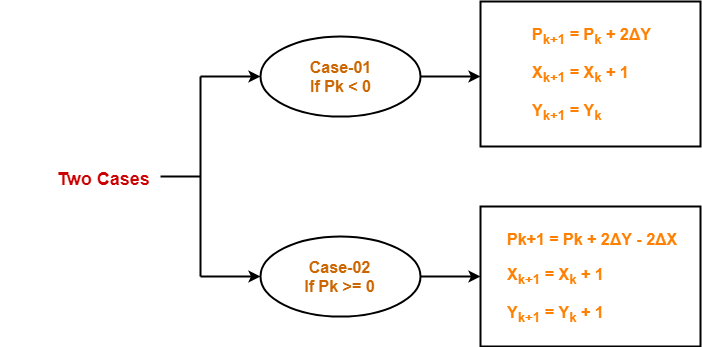
Pk = 2ΔY – ΔX
Step-03:
Suppose the current point is (Xk, Yk) and the next point is (Xk+1, Yk+1).
Find the next point depending on the value of decision parameter Pk.
Follow the below two cases-
Step-04:
Keep repeating Step-03 until the end point is reached or number of iterations equals to (ΔX-1) times.
PRACTICE PROBLEMS BASED ON BRESENHAM LINE DRAWING ALGORITHM-
Problem-01:
Calculate the points between the starting coordinates (9, 18) and ending coordinates (14, 22).
Solution-
Given-
- Starting coordinates = (X0, Y0) = (9, 18)
- Ending coordinates = (Xn, Yn) = (14, 22)
Step-01:
Calculate ΔX and ΔY from the given input.
- ΔX = Xn – X0 = 14 – 9 = 5
- ΔY =Yn – Y0 = 22 – 18 = 4
Step-02:
Calculate the decision parameter.
Pk
= 2ΔY – ΔX
= 2 x 4 – 5
= 3
So, decision parameter Pk = 3
Step-03:
As Pk >= 0, so case-02 is satisfied.
Thus,
- Pk+1 = Pk + 2ΔY – 2ΔX = 3 + (2 x 4) – (2 x 5) = 1
- Xk+1 = Xk + 1 = 9 + 1 = 10
- Yk+1 = Yk + 1 = 18 + 1 = 19
Similarly, Step-03 is executed until the end point is reached or number of iterations equals to 4 times.
(Number of iterations = ΔX – 1 = 5 – 1 = 4)
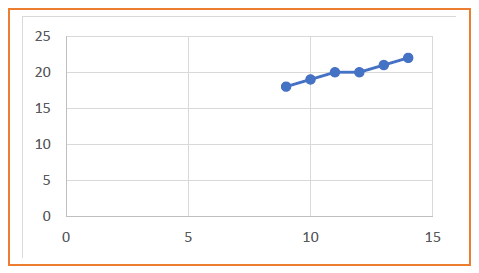
| Pk | Pk+1 | Xk+1 | Yk+1 |
| 9 | 18 | ||
| 3 | 1 | 10 | 19 |
| 1 | -1 | 11 | 20 |
| -1 | 7 | 12 | 20 |
| 7 | 5 | 13 | 21 |
| 5 | 3 | 14 | 22 |
Problem-02:
Calculate the points between the starting coordinates (20, 10) and ending coordinates (30, 18).
Solution-
Given-
- Starting coordinates = (X0, Y0) = (20, 10)
- Ending coordinates = (Xn, Yn) = (30, 18)
Step-01:
Calculate ΔX and ΔY from the given input.
- ΔX = Xn – X0 = 30 – 20 = 10
- ΔY =Yn – Y0 = 18 – 10 = 8
Step-02:
Calculate the decision parameter.
Pk
= 2ΔY – ΔX
= 2 x 8 – 10
= 6
So, decision parameter Pk = 6
Step-03:
As Pk >= 0, so case-02 is satisfied.
Thus,
- Pk+1 = Pk + 2ΔY – 2ΔX = 6 + (2 x 8) – (2 x 10) = 2
- Xk+1 = Xk + 1 = 20 + 1 = 21
- Yk+1 = Yk + 1 = 10 + 1 = 11
Similarly, Step-03 is executed until the end point is reached or number of iterations equals to 9 times.
(Number of iterations = ΔX – 1 = 10 – 1 = 9)
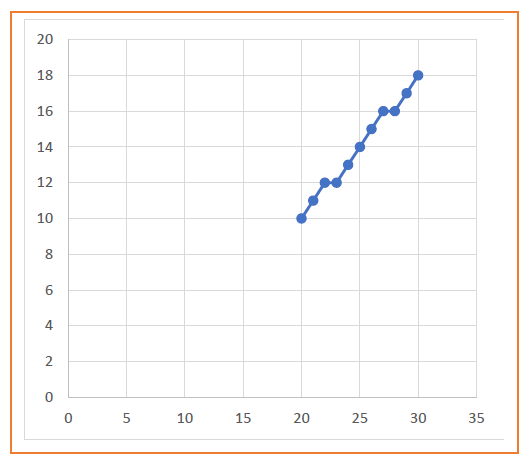
| Pk | Pk+1 | Xk+1 | Yk+1 |
| 20 | 10 | ||
| 6 | 2 | 21 | 11 |
| 2 | -2 | 22 | 12 |
| -2 | 14 | 23 | 12 |
| 14 | 10 | 24 | 13 |
| 10 | 6 | 25 | 14 |
| 6 | 2 | 26 | 15 |
| 2 | -2 | 27 | 16 |
| -2 | 14 | 28 | 16 |
| 14 | 10 | 29 | 17 |
| 10 | 6 | 30 | 18 |
Advantages of Bresenham Line Drawing Algorithm-
The advantages of Bresenham Line Drawing Algorithm are-
- It is easy to implement.
- It is fast and incremental.
- It executes fast but less faster than DDA Algorithm.
- The points generated by this algorithm are more accurate than DDA Algorithm.
- It uses fixed points only.
Disadvantages of Bresenham Line Drawing Algorithm-
The disadvantages of Bresenham Line Drawing Algorithm are-
- Though it improves the accuracy of generated points but still the resulted line is not smooth.
- This algorithm is for the basic line drawing.
- It can not handle diminishing jaggies.
To gain better understanding about Bresenham Line Drawing Algorithm,
Next Article- Mid Point Line Drawing Algorithm
Get more notes and other study material of Computer Graphics.
Watch video lectures by visiting our YouTube channel LearnVidFun.

