Binary Tree-
Before you go through this article, make sure that you gone through the previous article on Binary Trees.
We have discussed-
- Binary tree is a special tree data structure.
- In a binary tree, each node can have at most 2 children.
- In a binary tree, nodes may be arranged in any random order.
In this article, we will discuss about Binary Search Trees.
Binary Search Tree-
| Binary Search Tree is a special kind of binary tree in which nodes are arranged in a specific order. |
In a binary search tree (BST), each node contains-
- Only smaller values in its left sub tree
- Only larger values in its right sub tree
Example-
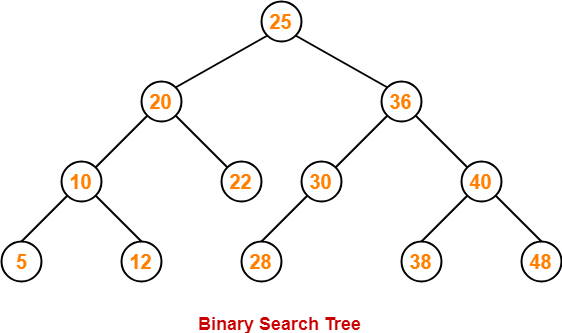
Number of Binary Search Trees-

Example-
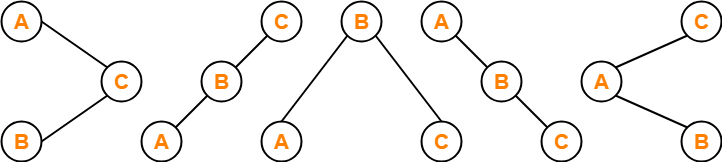
Number of distinct binary search trees possible with 3 distinct keys
= 2×3C3 / 3+1
= 6C3 / 4
= 5
If three distinct keys are A, B and C, then 5 distinct binary search trees are-
Binary Search Tree Construction-
Let us understand the construction of a binary search tree using the following example-
Example-
Construct a Binary Search Tree (BST) for the following sequence of numbers-
50, 70, 60, 20, 90, 10, 40, 100
When elements are given in a sequence,
- Always consider the first element as the root node.
- Consider the given elements and insert them in the BST one by one.
The binary search tree will be constructed as explained below-
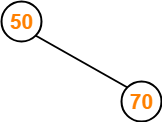
Insert 50-
![]()
Insert 70-
- As 70 > 50, so insert 70 to the right of 50.
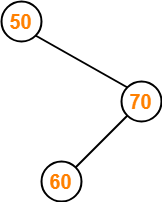
Insert 60-
- As 60 > 50, so insert 60 to the right of 50.
- As 60 < 70, so insert 60 to the left of 70.
Insert 20-
- As 20 < 50, so insert 20 to the left of 50.
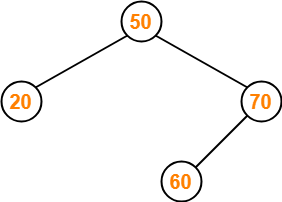
Insert 90-
- As 90 > 50, so insert 90 to the right of 50.
- As 90 > 70, so insert 90 to the right of 70.
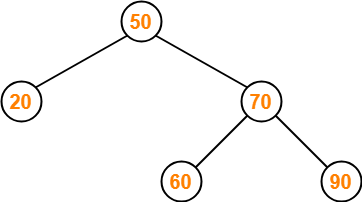
Insert 10-
- As 10 < 50, so insert 10 to the left of 50.
- As 10 < 20, so insert 10 to the left of 20.
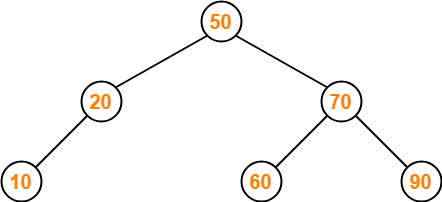
Insert 40-
- As 40 < 50, so insert 40 to the left of 50.
- As 40 > 20, so insert 40 to the right of 20.
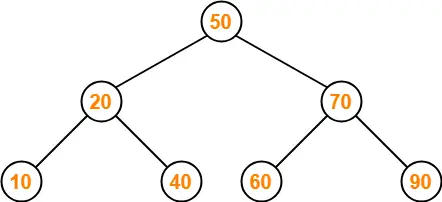
Insert 100-
- As 100 > 50, so insert 100 to the right of 50.
- As 100 > 70, so insert 100 to the right of 70.
- As 100 > 90, so insert 100 to the right of 90.
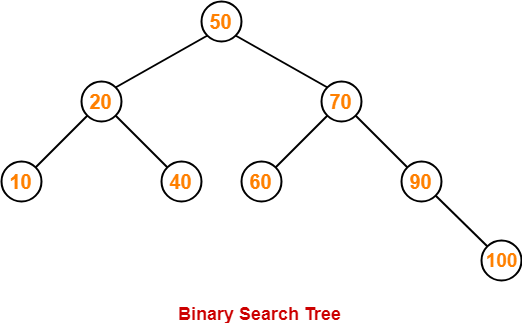
This is the required Binary Search Tree.
To gain better understanding about Binary Search Trees,
PRACTICE PROBLEMS BASED ON BINARY SEARCH TREES-
Problem-01:
A binary search tree is generated by inserting in order of the following integers-
50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24
The number of nodes in the left subtree and right subtree of the root respectively is _____.
- (4, 7)
- (7, 4)
- (8, 3)
- (3, 8)
Solution-
Using the above discussed steps, we will construct the binary search tree.
The resultant binary search tree will be-
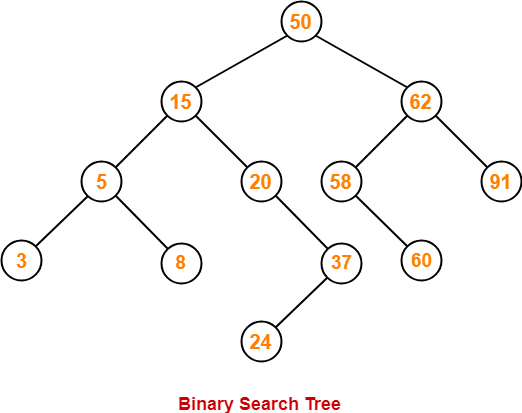
Clearly,
- Number of nodes in the left subtree of the root = 7
- Number of nodes in the right subtree of the root = 4
Thus, Option (B) is correct.
Problem-02:
How many distinct binary search trees can be constructed out of 4 distinct keys?
- 5
- 14
- 24
- 35
Solution-
Number of distinct binary search trees possible with 4 distinct keys
= 2nCn / n+1
= 2×4C4 / 4+1
= 8C4 / 5
= 14
Thus, Option (B) is correct.
Problem-03:
The numbers 1, 2, …, n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be-
- p
- p+1
- n-p
- n-p+1
Solution-
Let n = 4 and p = 3.
Then, given options reduce to-
- 3
- 4
- 1
- 2
Our binary search tree will be as shown-
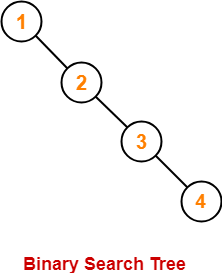
Clearly, first inserted number = 1.
Thus, Option (C) is correct.
Problem-04:
We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with given set so that it becomes a binary search tree?
- 0
- 1
- n!
- C(2n, n) / n+1
Solution-
Option (B) is correct.
To watch video solutions and practice more problems,
Download Handwritten Notes Here-
Next Article- Binary Search Tree Traversal
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.


